| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
m_kao_marko
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (21:05:03)
Postovi: (16)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 22:16 sri, 15. 12. 2010 Naslov: Re: 3. zadaca - 4.d) i 6. Postano: 22:16 sri, 15. 12. 2010 Naslov: Re: 3. zadaca - 4.d) i 6. |
    |
|
|
[quote="m_kao_marko"]U 4.d zadatku:
Dal ovaj niz ima limes + beskonacno?
log(logn)
ako je n prirodan onda je logn=[0,+beskonacno>, al tada log(logn) nije dobro definiran uopce..al ako se gleda samo da n-> onda bi bio lim beskonacno.. moze mi to netko pojasnit..[/quote]
Izraz [latex]\log \log n[/latex] nije definiran za [latex]n = 1[/latex], ali to ne smeta. Samo se dogovorimo da niz ne kreće od 1, već od, npr. 17. Ionako nam je za limes potrebno samo "ponašanje u beskonačnosti", tj. prvih konačno mnogo člana niza ne igra ulogu u limesu.
[quote="m_kao_marko"]6. Postoji li niz ciji je skup gomilista skup N? dokazi tvrdnju! -Pomoć??
hvala :D[/quote]
Da, npr. [latex](1, 1, 2, 1, 2, 3, 1, 2, 3, 4, 1, 2, 3, 4, 5, \ldots)[/latex]. Lako je pokazati da je svaki prirodan broj gomilište ovog niza. Samo se treba odabrati jedan podniz (najbolje uzeti onaj konstantni).
Dokazati da bilo koji drugi realni broj nije gomilište isto nije teško. Dovoljno je pronaći dovoljno malu okolinu koja ne sadrži niti jedan član niza.
Problemčić je što je i [latex]+\infty[/latex] gomilište tog niza, što nije prirodan broj. No, to se ne može izbjeći. Ako su nekom nizu gomilišta svi prirodni brojevi, onda je nekako očito da on ima strogo rastući podniz koji divergira u [latex]+\infty[/latex].
Znači, odgovor na postavljeno pitanje bi možda ipak trebao biti ne. :|
| m_kao_marko (napisa): | U 4.d zadatku:
Dal ovaj niz ima limes + beskonacno?
log(logn)
ako je n prirodan onda je logn=[0,+beskonacno>, al tada log(logn) nije dobro definiran uopce..al ako se gleda samo da n→ onda bi bio lim beskonacno.. moze mi to netko pojasnit.. |
Izraz 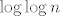 nije definiran za nije definiran za 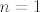 , ali to ne smeta. Samo se dogovorimo da niz ne kreće od 1, već od, npr. 17. Ionako nam je za limes potrebno samo "ponašanje u beskonačnosti", tj. prvih konačno mnogo člana niza ne igra ulogu u limesu. , ali to ne smeta. Samo se dogovorimo da niz ne kreće od 1, već od, npr. 17. Ionako nam je za limes potrebno samo "ponašanje u beskonačnosti", tj. prvih konačno mnogo člana niza ne igra ulogu u limesu.
| m_kao_marko (napisa): | 6. Postoji li niz ciji je skup gomilista skup N? dokazi tvrdnju! -Pomoć??
hvala  |
Da, npr.  . Lako je pokazati da je svaki prirodan broj gomilište ovog niza. Samo se treba odabrati jedan podniz (najbolje uzeti onaj konstantni). . Lako je pokazati da je svaki prirodan broj gomilište ovog niza. Samo se treba odabrati jedan podniz (najbolje uzeti onaj konstantni).
Dokazati da bilo koji drugi realni broj nije gomilište isto nije teško. Dovoljno je pronaći dovoljno malu okolinu koja ne sadrži niti jedan član niza.
Problemčić je što je i  gomilište tog niza, što nije prirodan broj. No, to se ne može izbjeći. Ako su nekom nizu gomilišta svi prirodni brojevi, onda je nekako očito da on ima strogo rastući podniz koji divergira u gomilište tog niza, što nije prirodan broj. No, to se ne može izbjeći. Ako su nekom nizu gomilišta svi prirodni brojevi, onda je nekako očito da on ima strogo rastući podniz koji divergira u  . .
Znači, odgovor na postavljeno pitanje bi možda ipak trebao biti ne. 
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
 Postano: 22:32 sri, 15. 12. 2010 Naslov: Re: 3. zadaca - 4.d) i 6. Postano: 22:32 sri, 15. 12. 2010 Naslov: Re: 3. zadaca - 4.d) i 6. |
    |
|
|
[quote="pmli"]
Problemčić je što je i [latex]+\infty[/latex] gomilište tog niza, što nije prirodan broj. No, to se ne može izbjeći. Ako su nekom nizu gomilišta svi prirodni brojevi, onda je nekako očito da on ima strogo rastući podniz koji divergira u [latex]+\infty[/latex].:|[/quote]
Ako se dogovorimo da samo konvergentni nizovi imaju limes, onda [latex]+\infty[/latex] nije gomilište. Ovisi dakle o definiciji limesa, zar ne?
| pmli (napisa): |
Problemčić je što je i  gomilište tog niza, što nije prirodan broj. No, to se ne može izbjeći. Ako su nekom nizu gomilišta svi prirodni brojevi, onda je nekako očito da on ima strogo rastući podniz koji divergira u gomilište tog niza, što nije prirodan broj. No, to se ne može izbjeći. Ako su nekom nizu gomilišta svi prirodni brojevi, onda je nekako očito da on ima strogo rastući podniz koji divergira u  . . |
Ako se dogovorimo da samo konvergentni nizovi imaju limes, onda  nije gomilište. Ovisi dakle o definiciji limesa, zar ne? nije gomilište. Ovisi dakle o definiciji limesa, zar ne?
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
Boris B.
Forumaš(ica)

Pridružen/a: 19. 01. 2010. (18:01:54)
Postovi: (32)16
Spol: 
|
 Postano: 12:00 pet, 17. 12. 2010 Naslov: Postano: 12:00 pet, 17. 12. 2010 Naslov: |
    |
|
|
Da, ali ne piše da se traži da N bude skup gomilišta kada se limesi, pa onda time po ovoj definiciji i gomilišta promatraju u R-potez, niti bih očekivao da je takvo tumačenje namjereno u ovom zadatku... (Ovisi zapravo ne toliko o definiciji limesa nego o prostoru gdje ga tražimo.)
No da, ako gledamo u R-potez, onda imamo niz podnizova koji konvergiraju u pripadne prirodne brojeve, pa možemo npr. od svakoga odabrati po jedan član koji je udaljen od n u kojeg niz konvergira za ε < 1/2, i tako dobivamo strogo rastući podniz kojemu je +oo limes.
Da, ali ne piše da se traži da N bude skup gomilišta kada se limesi, pa onda time po ovoj definiciji i gomilišta promatraju u R-potez, niti bih očekivao da je takvo tumačenje namjereno u ovom zadatku... (Ovisi zapravo ne toliko o definiciji limesa nego o prostoru gdje ga tražimo.)
No da, ako gledamo u R-potez, onda imamo niz podnizova koji konvergiraju u pripadne prirodne brojeve, pa možemo npr. od svakoga odabrati po jedan član koji je udaljen od n u kojeg niz konvergira za ε < 1/2, i tako dobivamo strogo rastući podniz kojemu je +oo limes.
_________________
The lyf so short, the craft so long to lerne
|
|
| [Vrh] |
|
kapetan
Forumaš(ica)

Pridružen/a: 03. 11. 2010. (00:01:56)
Postovi: (2)16
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
|
| [Vrh] |
|
|








