| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
shimija
Forumaš(ica)


Pridružen/a: 22. 01. 2007. (18:33:54)
Postovi: (138)16
Spol: 
Lokacija: Spljit
|
|
| [Vrh] |
|
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
 Postano: 19:40 uto, 21. 12. 2010 Naslov: Postano: 19:40 uto, 21. 12. 2010 Naslov: |
    |
|
|
Nemogu ovako:
[latex]\frac{12m-n-3mn+7}{(m+1)(5-2n)}=\frac{3m(4-n)+(4-n)+3}{(m+1)(5-2n)}=\frac{(3m+1)(4-n)+3}{(m+1)(5-2n)}[/latex]
i sad razdvojim na skupove...
[latex]{\frac{3m+1}{m+1}},{\frac{4-n}{5-2n}},{\frac{3}{m+1}},{\frac{1}{5-2n}}[/latex]
nije sad ako redom oznacim s1,s2,s3,s4...
S=(s1*s2)+(s3*s4)???
Ne kuzim zasto takav rastav skupa...
Moze objasnjenje? hvala, mozda je banalno i glupo, al zalomilo mi se... :)
Nemogu ovako:
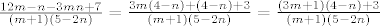
i sad razdvojim na skupove...
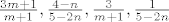
nije sad ako redom oznacim s1,s2,s3,s4...
S=(s1*s2)+(s3*s4)???
Ne kuzim zasto takav rastav skupa...
Moze objasnjenje? hvala, mozda je banalno i glupo, al zalomilo mi se... 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 21:23 uto, 21. 12. 2010 Naslov: Postano: 21:23 uto, 21. 12. 2010 Naslov: |
    |
|
|
@CROmpir: Uzmimo neki jednostavniji primjer. Neka je [latex]S = \{ 1 \}[/latex]. Očito [latex]\inf S = \sup S = 1[/latex]. Promotrimo [latex]A = \{ n + 1 : n \in \mathbb{N} \}[/latex] i [latex]B = \{ -n : n \in \mathbb{N} \}[/latex]. Također je očito da je [latex]\inf A = 2[/latex], [latex]\inf B = -\infty[/latex], [latex]\sup A = +\infty[/latex] i [latex]\sup B = -1[/latex]. Slijedi da je [latex]\inf (A + B) = -\infty[/latex] i [latex]\sup (A + B) = +\infty[/latex]. Jasno je [latex]S \neq A + B[/latex].
U tome je problem, ne znaš unaprijed kako se ponaša zbroj skupova kad imaju nešto zajedničko.
Shimija je predložio odličnu ideju. :D Podsjeća na rastav na parcijalne razlomke. Problem je što matrica sustava, koja se dobi množenjem s nazivnicima i izjednačivanjem koeficijenata uz iste izraze, nije regularna. Dakle, za neke koeficijente neće postojati rješenja, a za druge će biti parametarska. :( Srećom, ovdje ima rješenja, npr. [latex](A, B, C, D) = (2, 1, 1, 2)[/latex]. Dakle, [latex]\displaystyle \frac{12 m - n - 3 m n + 7}{(m + 1)(5 - 2n)} = \frac{2 m + 1}{m + 1} + \frac{n + 2}{5 - 2 n}[/latex].
@CROmpir: Uzmimo neki jednostavniji primjer. Neka je 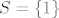 . Očito . Očito 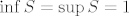 . Promotrimo . Promotrimo 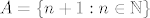 i i 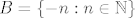 . Također je očito da je . Također je očito da je 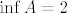 , , 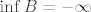 , , 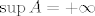 i i 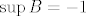 . Slijedi da je . Slijedi da je 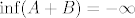 i i 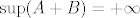 . Jasno je . Jasno je 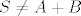 . .
U tome je problem, ne znaš unaprijed kako se ponaša zbroj skupova kad imaju nešto zajedničko.
Shimija je predložio odličnu ideju.  Podsjeća na rastav na parcijalne razlomke. Problem je što matrica sustava, koja se dobi množenjem s nazivnicima i izjednačivanjem koeficijenata uz iste izraze, nije regularna. Dakle, za neke koeficijente neće postojati rješenja, a za druge će biti parametarska. Podsjeća na rastav na parcijalne razlomke. Problem je što matrica sustava, koja se dobi množenjem s nazivnicima i izjednačivanjem koeficijenata uz iste izraze, nije regularna. Dakle, za neke koeficijente neće postojati rješenja, a za druge će biti parametarska.  Srećom, ovdje ima rješenja, npr. Srećom, ovdje ima rješenja, npr. 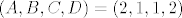 . Dakle, . Dakle, 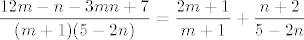 . .
|
|
| [Vrh] |
|
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
 Postano: 17:10 uto, 28. 12. 2010 Naslov: Postano: 17:10 uto, 28. 12. 2010 Naslov: |
    |
|
|
/molim te objasni mi kako da to tocno napravim. Pocnimo gledati od n=3, dakle, y<0. Sto cemo sada za 1≤n<3?
[size=9][color=#999999]Added after 11 minutes:[/color][/size]
[quote="satja"][quote="c4rimson"]moze pomoc oko 8. zadatka?[/quote]
Neka je [latex]q = \displaystyle \frac m n[/latex], i onda zapiši zadani razlomak samo pomoću [latex]q[/latex]. Imajući na umu da je [latex]q[/latex] bilo koji pozitivan racionalan broj, lako ćeš zaključiti što su supremum i infimum dobivenog izraza.[/quote]
inf je 1/5, a nije omeden odozgo?
ili....
/molim te objasni mi kako da to tocno napravim. Pocnimo gledati od n=3, dakle, y<0. Sto cemo sada za 1≤n<3?
Added after 11 minutes:
| satja (napisa): | | c4rimson (napisa): | | moze pomoc oko 8. zadatka? |
Neka je 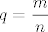 , i onda zapiši zadani razlomak samo pomoću , i onda zapiši zadani razlomak samo pomoću  . Imajući na umu da je . Imajući na umu da je  bilo koji pozitivan racionalan broj, lako ćeš zaključiti što su supremum i infimum dobivenog izraza. bilo koji pozitivan racionalan broj, lako ćeš zaključiti što su supremum i infimum dobivenog izraza. |
inf je 1/5, a nije omeden odozgo?
ili....
|
|
| [Vrh] |
|
|











