| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 22:22 pet, 17. 12. 2010 Naslov: Postano: 22:22 pet, 17. 12. 2010 Naslov: |
    |
|
|
[latex]F(x, y, z) = 3 x^2 - y + 5 z[/latex], [latex]{\sf grad} \, F(x, y, z) = (6 x, -1, 5)[/latex]
Vektori normala dviju zadanih ravnina su [latex](2, 1, -1)[/latex] i [latex](2, -1, 3)[/latex]. Slijedi da je vektor smjera pravca određenim tim ravninama [latex]\left|\begin{array}{ccc}
\vec{i} & \vec{j} & \vec{k} \\
2 & 1 & -1 \\
2 & -1 & 3
\end{array}\right| = (2, -8, -4) = 2 (1, -4, -2)[/latex]. Da bi ravnina bila paralelna s pravcem, mora vektor normale ravnine biti okomit na vektor smjera pravca. Dakle, treba vrijedi [latex]((6 x, -1, 5) | (1, -4, -2)) = 0[/latex]. To vrijedi akko [latex]x = 1[/latex]. Znači, skup tih točaka je [latex]\{ (1, y, z) : 3 - y + 5 z = 0 \} = \{ (1, 5 z + 3, z) : z \in \mathbb{R} \}[/latex]. Treba odrediti [latex]z[/latex] td. je udaljenost točke [latex](1, 5 z + 3, z)[/latex] od ishodišta minimalna, a to je ekvivalentno s tim da je kvadrat udaljenosti minimalan. Kvadrat udaljenosti te točke od ishodišta je [latex]1 + (5 z + 3)^2 + z^2 = 6 z^2 + 30 z + 10[/latex]. Iz srednje škole znamo da se minimum postiže za [latex]z = -\dfrac{30}{2 \cdot 6} = -\dfrac{5}{2}[/latex].
Dakle, tražena točka je [latex]\displaystyle \left(1, -\frac{19}{2}, -\frac{5}{2}\right)[/latex].
 , , 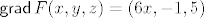
Vektori normala dviju zadanih ravnina su 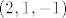 i i 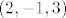 . Slijedi da je vektor smjera pravca određenim tim ravninama . Slijedi da je vektor smjera pravca određenim tim ravninama  . Da bi ravnina bila paralelna s pravcem, mora vektor normale ravnine biti okomit na vektor smjera pravca. Dakle, treba vrijedi . Da bi ravnina bila paralelna s pravcem, mora vektor normale ravnine biti okomit na vektor smjera pravca. Dakle, treba vrijedi 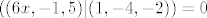 . To vrijedi akko . To vrijedi akko  . Znači, skup tih točaka je . Znači, skup tih točaka je 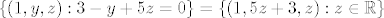 . Treba odrediti . Treba odrediti  td. je udaljenost točke td. je udaljenost točke 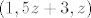 od ishodišta minimalna, a to je ekvivalentno s tim da je kvadrat udaljenosti minimalan. Kvadrat udaljenosti te točke od ishodišta je od ishodišta minimalna, a to je ekvivalentno s tim da je kvadrat udaljenosti minimalan. Kvadrat udaljenosti te točke od ishodišta je 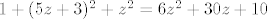 . Iz srednje škole znamo da se minimum postiže za . Iz srednje škole znamo da se minimum postiže za 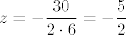 . .
Dakle, tražena točka je 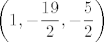 . .
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
šišmiš
Forumaš(ica)

Pridružen/a: 19. 04. 2010. (21:01:19)
Postovi: (29)16
|
|
| [Vrh] |
|
studentica.
Gost
|
|
| [Vrh] |
|
Boris B.
Forumaš(ica)

Pridružen/a: 19. 01. 2010. (18:01:54)
Postovi: (32)16
Spol: 
|
 Postano: 1:45 pon, 3. 1. 2011 Naslov: Postano: 1:45 pon, 3. 1. 2011 Naslov: |
    |
|
|
[quote="šišmiš"]http://web.math.hr/nastava/difraf/dif/2006-07/zadaca3.pdf
moze pomoc oko: 5,6 i 10 zadatka..
u 10 neznam kaj da radim uopce, koje parcijalne derivacije da trazim..zbuljen sam :S
hvala :)[/quote]
5. Nisam uspio naći ništa bolje od Observationa 3.6 ovdje: [url]www.physics.it/lectures/analysis_course_1.ps[/url].
6. Ne mora, jer ne mora biti ni neprekidna. Recimo, neka je f(x, y) = 0 na R\{0, 0}, a 1 za (0, 0). Funkcija ima maksimum u (0, 0), ali nije neprekidna, pa ni diferencijabilna u njoj.
Ali vrijedi i za neprekidne funkcije, npr. -|x| ima maksimum, ali nema diferencijal u 0.
10. Kao i inače tražiš parcijalne derivacije po x i po y. [latex]\partial_x f = 2x \sin \frac 1 x -\cos \frac 1 x, x \neq 0[/latex] i [latex]\partial_x f = 0, x = 0[/latex]. Parc. derivacija po y je naravno 2y za sve (x, y) iz R^2. Pošto parcijalna derivacija po x (zbog kosinusa) nema limesa kada x -> 0, parcijalne derivacije nisu neprekidne. No, (0, 2y) ipak je diferencijal u točkama oblika (0, y), što provjeriš računanjem limesa iz definicije diferencijala.
Ako trebaju a) dio i detalji o ovome, raspišem.
| šišmiš (napisa): | http://web.math.hr/nastava/difraf/dif/2006-07/zadaca3.pdf
moze pomoc oko: 5,6 i 10 zadatka..
u 10 neznam kaj da radim uopce, koje parcijalne derivacije da trazim..zbuljen sam :S
hvala  |
5. Nisam uspio naći ništa bolje od Observationa 3.6 ovdje: www.physics.it/lectures/analysis_course_1.ps.
6. Ne mora, jer ne mora biti ni neprekidna. Recimo, neka je f(x, y) = 0 na R\{0, 0}, a 1 za (0, 0). Funkcija ima maksimum u (0, 0), ali nije neprekidna, pa ni diferencijabilna u njoj.
Ali vrijedi i za neprekidne funkcije, npr. -|x| ima maksimum, ali nema diferencijal u 0.
10. Kao i inače tražiš parcijalne derivacije po x i po y. 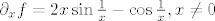 i i 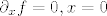 . Parc. derivacija po y je naravno 2y za sve (x, y) iz R^2. Pošto parcijalna derivacija po x (zbog kosinusa) nema limesa kada x → 0, parcijalne derivacije nisu neprekidne. No, (0, 2y) ipak je diferencijal u točkama oblika (0, y), što provjeriš računanjem limesa iz definicije diferencijala. . Parc. derivacija po y je naravno 2y za sve (x, y) iz R^2. Pošto parcijalna derivacija po x (zbog kosinusa) nema limesa kada x → 0, parcijalne derivacije nisu neprekidne. No, (0, 2y) ipak je diferencijal u točkama oblika (0, y), što provjeriš računanjem limesa iz definicije diferencijala.
Ako trebaju a) dio i detalji o ovome, raspišem.
_________________
The lyf so short, the craft so long to lerne
|
|
| [Vrh] |
|
šišmiš
Forumaš(ica)

Pridružen/a: 19. 04. 2010. (21:01:19)
Postovi: (29)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 12:38 pon, 3. 1. 2011 Naslov: Postano: 12:38 pon, 3. 1. 2011 Naslov: |
    |
|
|
U 15 imamo diferencijabilnu funkciju (f) komponiranu sa linearnim operatorom, h(x)=<x,v>. Sada imamo [latex]g=h \circ f[/latex], a
za diferencijal kompozicije imamo lancano pravilo
Dg(x)=Dh(f(x))Df(x).
Kako je h linearan operator, znamo Dh(c)=h za svaku tocku c.
Iz toga imamo [latex]Dg(x)=h \circ Df(x)[/latex], tj. [latex]Dg(x)=\langle Df(x),v \rangle[/latex].
U 18, da sve bude formalno, mozemo (kao sto i pise) identificirati Rn x Rn s R(2n) pa (x,y) shvatiti kao jedan vektor (npr h), a onda pisati x i y kao projekcije od h:
x=p1(h)
y=p2(h)
p1 je projekcija na prvih n koord, p2 na drugih n, oboje su linearni operatori.
Sad funkciju mozemo zapisati kao
[latex]f(h)=p_1(h)e^{\langle p_2(h),v_0\rangle}[/latex]
Tu imamo neki umnozak vektorske (to je p1) i skalarne (e^...) funkcije, pa za trazenje diferencijala mozemo koristiti pravilo za diferencijal produkta:
Dfg(c)=Df(c)g(c) + f(c)Dg(c)
U 15 imamo diferencijabilnu funkciju (f) komponiranu sa linearnim operatorom, h(x)=<x,v>. Sada imamo  , a , a
za diferencijal kompozicije imamo lancano pravilo
Dg(x)=Dh(f(x))Df(x).
Kako je h linearan operator, znamo Dh(c)=h za svaku tocku c.
Iz toga imamo 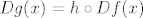 , tj. , tj. 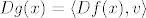 . .
U 18, da sve bude formalno, mozemo (kao sto i pise) identificirati Rn x Rn s R(2n) pa (x,y) shvatiti kao jedan vektor (npr h), a onda pisati x i y kao projekcije od h:
x=p1(h)
y=p2(h)
p1 je projekcija na prvih n koord, p2 na drugih n, oboje su linearni operatori.
Sad funkciju mozemo zapisati kao
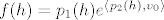
Tu imamo neki umnozak vektorske (to je p1) i skalarne (e^...) funkcije, pa za trazenje diferencijala mozemo koristiti pravilo za diferencijal produkta:
Dfg(c)=Df(c)g(c) + f(c)Dg(c)
|
|
| [Vrh] |
|
šišmiš
Forumaš(ica)

Pridružen/a: 19. 04. 2010. (21:01:19)
Postovi: (29)16
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 16:13 pon, 3. 1. 2011 Naslov: Postano: 16:13 pon, 3. 1. 2011 Naslov: |
    |
|
|
mislim da tako i trebaš dobit :?:
pogledaj malo f-ju, veća je od 0 za sve x,y,z,da nema uvjeta minimum bi se postizao u nuli, ovako u tim točkama jer se predznak gubi zbog parnih potencija(pa ih ima više)
nisam rješavala,ali mi se čini da je tako!
mislim da tako i trebaš dobit 
pogledaj malo f-ju, veća je od 0 za sve x,y,z,da nema uvjeta minimum bi se postizao u nuli, ovako u tim točkama jer se predznak gubi zbog parnih potencija(pa ih ima više)
nisam rješavala,ali mi se čini da je tako!
|
|
| [Vrh] |
|
šišmiš
Forumaš(ica)

Pridružen/a: 19. 04. 2010. (21:01:19)
Postovi: (29)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
šišmiš
Forumaš(ica)

Pridružen/a: 19. 04. 2010. (21:01:19)
Postovi: (29)16
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
šišmiš
Forumaš(ica)

Pridružen/a: 19. 04. 2010. (21:01:19)
Postovi: (29)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
šišmiš
Forumaš(ica)

Pridružen/a: 19. 04. 2010. (21:01:19)
Postovi: (29)16
|
|
| [Vrh] |
|
|











