| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
 Postano: 21:01 sub, 27. 11. 2010 Naslov: Slučajne varijable- zadaci Postano: 21:01 sub, 27. 11. 2010 Naslov: Slučajne varijable- zadaci |
    |
|
|
Molim za pomoć sa par zadataka koji se nalaze ovdje http://web.math.hr/nastava/uuv/files/chap4.pdf
4.25. pod b) sam dobila [latex]\frac{1}{1-(1-p_1)(1-p_2)}-1[/latex] , je li to dobro? nekako mi je čudno... kako bi se riješilo pod c) ?
4.29. uz tako definirane varijable, [latex]S_2[/latex] bi bio jednak [latex]2X_1[/latex] pa bi poprimao vrijedndosti -2 i 2. zašto se onda spominje nula, tj [latex]S\in\{-2, 0, 2\}[/latex] ? bi li netko htio riješiti c) dio tako da po tome riješim ostale?
4.35. krenula sam po standardnom postupku, tj traženje nultočaka funkcije i dalje ne znam što bih
4.44. dobijem [latex]\displaystyle\sum_{k=1}^{\infty}\frac{1}{k}(1-p)^k[/latex], ne znam što s tim :(
Molim za pomoć sa par zadataka koji se nalaze ovdje http://web.math.hr/nastava/uuv/files/chap4.pdf
4.25. pod b) sam dobila 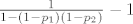 , je li to dobro? nekako mi je čudno... kako bi se riješilo pod c) ? , je li to dobro? nekako mi je čudno... kako bi se riješilo pod c) ?
4.29. uz tako definirane varijable, 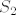 bi bio jednak bi bio jednak 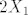 pa bi poprimao vrijedndosti -2 i 2. zašto se onda spominje nula, tj pa bi poprimao vrijedndosti -2 i 2. zašto se onda spominje nula, tj 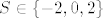 ? bi li netko htio riješiti c) dio tako da po tome riješim ostale? ? bi li netko htio riješiti c) dio tako da po tome riješim ostale?
4.35. krenula sam po standardnom postupku, tj traženje nultočaka funkcije i dalje ne znam što bih
4.44. dobijem 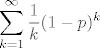 , ne znam što s tim , ne znam što s tim 
_________________
Granice mogućega možemo odrediti samo onda ako ih prijeđemo odlaskom u nemoguće
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 23:01 sub, 27. 11. 2010 Naslov: Re: Slučajne varijable- zadaci Postano: 23:01 sub, 27. 11. 2010 Naslov: Re: Slučajne varijable- zadaci |
    |
|
|
[quote="komaPMF"]4.25. pod b) sam dobila [latex]\frac{1}{1-(1-p_1)(1-p_2)}-1[/latex] , je li to dobro? nekako mi je čudno... kako bi se riješilo pod c) ?[/quote]
U b) sam dobio isto, samo bez -1. Za c) primjeti da je
[latex]\displaystyle $\begin{align*}
\mathbb{P}(X \geq 2 Y) & = \mathbb{P} \left( \bigcup_{n = 1}^{\infty} (Y = n, X \geq 2 n) \right) = \sum_{n = 1}^{\infty} \mathbb{P}(Y = n) \mathbb{P}(X \geq 2 n) = \sum_{n = 1}^{\infty} \mathbb{P}(Y = n) \mathbb{P} \left( \bigcup_{k = 2 n} X = k \right) \\
& = \sum_{n = 1}^{\infty} \mathbb{P}(Y = n) \sum_{k = 2n}^{\infty} \mathbb{P}(X = k)
\end{align*}$[/latex]
[quote="komaPMF"]4.29. uz tako definirane varijable, [latex]S_2[/latex] bi bio jednak [latex]2X_1[/latex] pa bi poprimao vrijedndosti -2 i 2. zašto se onda spominje nula, tj [latex]S\in\{-2, 0, 2\}[/latex] ? bi li netko htio riješiti c) dio tako da po tome riješim ostale?[/quote]
[latex]X_1[/latex] i [latex]X_2[/latex] nisu iste stvari. U toj priči se skriva neki [latex]\Omega[/latex], a [latex]X_1[/latex] i [latex]X_2[/latex] su nekako definirane na elementima [latex]\omega \in \Omega[/latex], na neki nepoznat način. Samo im znamo tablice distribucije.
No, očito je [latex]S_2 \in \{ -2, 0, 2 \} = \Omega[/latex] (siguran događaj), pa se u (a) zapravo traži [latex]\mathbb{P}(S_3 = 3)[/latex] (lako se vidi iz definicije uvjetne vjerojatnosti). Vidimo da je [latex]$\begin{align*} \mathbb{P}(S_3 = 3) = \mathbb{P}(X_1 + X_2 + X_3 = 3) = \mathbb{P}(X_1 = 1, X_2 = 1, X_3 = 1) = \mathbb{P}(X_1 = 1) \mathbb{P}(X_2 = 1) \mathbb{P}(X_3 = 1) = \frac{1}{8} \end{align*}$[/latex].
Nadam se da sam dovoljno pojasnio stvari da možeš riješiti preostale zadatke.
[quote="komaPMF"]4.35. krenula sam po standardnom postupku, tj traženje nultočaka funkcije i dalje ne znam što bih[/quote]
[latex]\mathbb{E}[(X - a)^2] = \mathbb{E}[X^2 - 2 a X + a^2] = \mathbb{E}[X^2] - 2 a \mathbb{E}[X] + a^2[/latex]. To je kvadratna funkcija po [latex]a[/latex]. Znamo da se minimum postiže za [latex]a = \mathbb{E}[X][/latex] ([latex]-\frac{b}{2 a}[/latex]). Kad to uvrstimo, dobivamo [latex]\mathbb{E}[X^2] - 2 (\mathbb{E}[X])^2 + (\mathbb{E}[X])^2 = \mathbb{E}[X^2] - (\mathbb{E}[X])^2 = {\sf Var} X[/latex].
[quote="komaPMF"]4.44. dobijem [latex]\displaystyle\sum_{k=1}^{\infty}\frac{1}{k}(1-p)^k[/latex], ne znam što s tim :([/quote]
Vjerojatno misliš [latex]\displaystyle \sum_{k = 1}^{\infty} \frac{1}{k} (1 - p)^{k - 1} p = p \sum_{k = 0}^{\infty} \frac{(1 - p)^k}{k + 1}[/latex]. Treba se prisjetiti MA2.
[latex]\displaystyle $\begin{align*}
\sum_{k = 0}^{\infty} x^k & = \frac{1}{1 - x} & / \int \\
\sum_{k = 0}^{\infty} \frac{x^{k + 1}}{k + 1} & = -\ln(1 - x) & / : x \\
\sum_{k = 0}^{\infty} \frac{x^k}{k + 1} & = -\frac{\ln(1 - x)}{x} & / x = 1 - p \\
\sum_{k = 0}^{\infty} \frac{(1 - p)^k}{k + 1} & = -\frac{\ln p}{1 - p}
\end{align*}$[/latex]
Dakle, [latex]\displaystyle \mathbb{E} \left[ \frac{1}{X} \right] = -\frac{p \ln p}{1 - p}[/latex]
| komaPMF (napisa): | 4.25. pod b) sam dobila 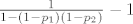 , je li to dobro? nekako mi je čudno... kako bi se riješilo pod c) ? , je li to dobro? nekako mi je čudno... kako bi se riješilo pod c) ? |
U b) sam dobio isto, samo bez -1. Za c) primjeti da je
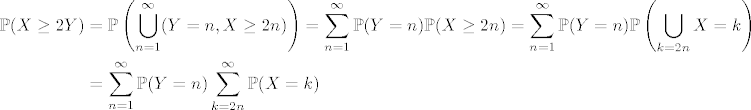
| komaPMF (napisa): | 4.29. uz tako definirane varijable, 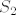 bi bio jednak bi bio jednak 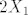 pa bi poprimao vrijedndosti -2 i 2. zašto se onda spominje nula, tj pa bi poprimao vrijedndosti -2 i 2. zašto se onda spominje nula, tj 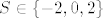 ? bi li netko htio riješiti c) dio tako da po tome riješim ostale? ? bi li netko htio riješiti c) dio tako da po tome riješim ostale? |
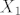 i i 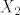 nisu iste stvari. U toj priči se skriva neki nisu iste stvari. U toj priči se skriva neki 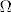 , a , a 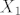 i i 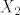 su nekako definirane na elementima su nekako definirane na elementima 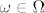 , na neki nepoznat način. Samo im znamo tablice distribucije. , na neki nepoznat način. Samo im znamo tablice distribucije.
No, očito je 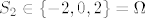 (siguran događaj), pa se u (a) zapravo traži (siguran događaj), pa se u (a) zapravo traži 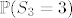 (lako se vidi iz definicije uvjetne vjerojatnosti). Vidimo da je (lako se vidi iz definicije uvjetne vjerojatnosti). Vidimo da je 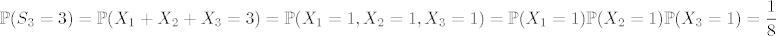 . .
Nadam se da sam dovoljno pojasnio stvari da možeš riješiti preostale zadatke.
| komaPMF (napisa): | | 4.35. krenula sam po standardnom postupku, tj traženje nultočaka funkcije i dalje ne znam što bih |
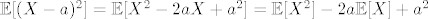 . To je kvadratna funkcija po . To je kvadratna funkcija po  . Znamo da se minimum postiže za . Znamo da se minimum postiže za 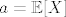 ( (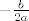 ). Kad to uvrstimo, dobivamo ). Kad to uvrstimo, dobivamo 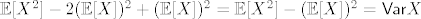 . .
| komaPMF (napisa): | 4.44. dobijem 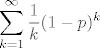 , ne znam što s tim , ne znam što s tim  |
Vjerojatno misliš 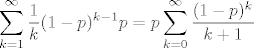 . Treba se prisjetiti MA2. . Treba se prisjetiti MA2.
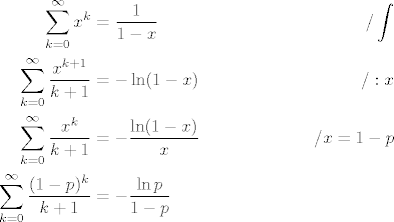
Dakle, 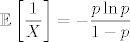
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
 Postano: 1:30 ned, 28. 11. 2010 Naslov: Postano: 1:30 ned, 28. 11. 2010 Naslov: |
    |
|
|
imam još jedno pitanje...
4.46. a) stavim da mi je X slučajna varijabla koja poprima vrijednosti iz skupa {5, 6, 7, ...} i za svaku je pripadna vjerojatnost [latex]\mathbb{P}(X=k+4)=(1-p)^{k-1}p, k=1, 2, ...[/latex]
dobijem da je matematičko očekivanje te varijable [latex]\frac{1}{p}+4[/latex], a u rješenjima je [latex]\frac{1}{1-p}+4[/latex]
Kako bi išlo pod b) ?
imam još jedno pitanje...
4.46. a) stavim da mi je X slučajna varijabla koja poprima vrijednosti iz skupa {5, 6, 7, ...} i za svaku je pripadna vjerojatnost 
dobijem da je matematičko očekivanje te varijable 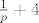 , a u rješenjima je , a u rješenjima je 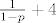
Kako bi išlo pod b) ?
_________________
Granice mogućega možemo odrediti samo onda ako ih prijeđemo odlaskom u nemoguće
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 2:45 ned, 28. 11. 2010 Naslov: Postano: 2:45 ned, 28. 11. 2010 Naslov: |
    |
|
|
Vjerojatnost pobjede je [latex]p[/latex], dakle, vjerojatnost da ćemo odigrati [latex]k \in \left\{5,\, 6,\, \ldots \right\}[/latex] igara je [latex]p^{k-5} \cdot \left(1-p\right)[/latex], sada izračunaš očekivanje te varijable i dobiješ točno [latex]\frac{1}{1-p} + 4[/latex].
b) dio, očekivani broj gubitaka nakon 4. igre je točno 1, dakle, traženo očekivanje je zapravo jednako očekivanom broju gubitaka u prve 4 igre uvećanom za 1. Očekivani broj gubitaka u prve 4 igre je zapravo očekivanje slučajne varijable koja poprima vrijednosti [latex]k \in \left\{0,\, 1,\, 2,\, 3,\, 4\right\}[/latex] s vjerojatnostima [latex]{4 \choose k} \cdot \left(1-p\right)^k \cdot p^{4-k}[/latex]. Ako se ne varam, traženo ukupno očekivanje je [latex]5-4p[/latex].
Vjerojatnost pobjede je  , dakle, vjerojatnost da ćemo odigrati , dakle, vjerojatnost da ćemo odigrati 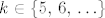 igara je igara je 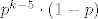 , sada izračunaš očekivanje te varijable i dobiješ točno , sada izračunaš očekivanje te varijable i dobiješ točno 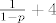 . .
b) dio, očekivani broj gubitaka nakon 4. igre je točno 1, dakle, traženo očekivanje je zapravo jednako očekivanom broju gubitaka u prve 4 igre uvećanom za 1. Očekivani broj gubitaka u prve 4 igre je zapravo očekivanje slučajne varijable koja poprima vrijednosti 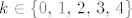 s vjerojatnostima s vjerojatnostima 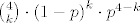 . Ako se ne varam, traženo ukupno očekivanje je . Ako se ne varam, traženo ukupno očekivanje je 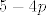 . .
|
|
| [Vrh] |
|
NeonBlack
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (15:46:24)
Postovi: (37)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
NeonBlack
Forumaš(ica)

Pridružen/a: 13. 10. 2009. (15:46:24)
Postovi: (37)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 23:14 uto, 14. 12. 2010 Naslov: Postano: 23:14 uto, 14. 12. 2010 Naslov: |
    |
|
|
Govoriš o 4.38?
[latex]\Omega = \{ 1, 2, \ldots, n \}^2[/latex]. [latex]\{X = k\} = \{ 1, 2, \ldots, k - 1 \} \times \{ k \} \cup \{ k \} \times \{ 1, 2, \ldots, k - 1 \} \cup \{ (k, k) \}[/latex]. Očito je [latex]|\{X = k\}| = k - 1 + k - 1 + 1 = 2 k - 1[/latex]. Dakle, [latex]\mathbb{P}(X = k) = \dfrac{2 k - 1}{n^2}[/latex].
Govoriš o 4.38?
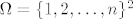 . . 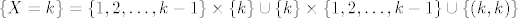 . Očito je . Očito je  . Dakle, . Dakle, 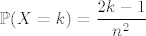 . .
|
|
| [Vrh] |
|
tmarusca
Forumaš(ica)


Pridružen/a: 28. 06. 2009. (20:53:52)
Postovi: (59)16
Spol: 
Lokacija: 1/039
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
tmarusca
Forumaš(ica)


Pridružen/a: 28. 06. 2009. (20:53:52)
Postovi: (59)16
Spol: 
Lokacija: 1/039
|
|
| [Vrh] |
|
tmarusca
Forumaš(ica)


Pridružen/a: 28. 06. 2009. (20:53:52)
Postovi: (59)16
Spol: 
Lokacija: 1/039
|
 Postano: 17:25 sub, 25. 12. 2010 Naslov: Postano: 17:25 sub, 25. 12. 2010 Naslov: |
    |
|
|
[quote="pmli"]4.40.
[latex]\displaystyle $\begin{align*}
\sum_{n = 1}^{\infty} \mathbb{P}(X^2 > n)
& = \sum_{n = 1}^{\infty} \mathbb{P}(X > \sqrt{n})
= \sum_{n = 1}^{\infty} \mathbb{P}(X \geq \lfloor \sqrt{n} \rfloor + 1)
= \sum_{n = 1}^{\infty} \sum_{k = \lfloor \sqrt{n} \rfloor + 1}^{\infty} \mathbb{P}(X = k) \\
& = \sum_{n = 1}^{\infty} \sum_{k = \lfloor \sqrt{n} \rfloor + 1}^{\infty} p (1 - p)^{k - 1}
= p \sum_{n = 1}^{\infty} \sum_{k = 0}^{\infty} (1 - p)^{k + \lfloor \sqrt{n} \rfloor + 1 - 1}
= p \sum_{n = 1}^{\infty} (1 - p)^{\lfloor \sqrt{n} \rfloor} \sum_{k = 0}^{\infty} (1 - p)^k \\
& = p \sum_{n = 1}^{\infty} (1 - p)^{\lfloor \sqrt{n} \rfloor} \frac{1}{p}
\stackrel{(*)}{=} \sum_{n = 1}^{\infty} (2 n + 1) (1 - p)^n
= ({\sf redovi})
= \frac{2 - p - p^2}{p^2}
\end{align*}[/latex]
Jednakost (*) se može naslutiti iz tablice
[table=;]
n;1;2;3;4;5;6;7;8;9;10;...
floor(sqrt(n));1;1;1;2;2;2;2;2;3;3;...
[/table][/quote]
ja sam tu isao drugom logikom, puno jednostavnije, ali nisam dobio isto rjesenje. mozes molim te naci gresku?
[latex]\displaystyle
X\sim G(p)\\
\sum_{n\in\mathbb{N}} P(X^2>n)=1 \overset{Zad. 4.20}{\iff} \mathbb{E}[X^2]=1\\
\mathbb{E}X=\frac{1}{p}\\
Var\ X=\mathbb{E}[X^2]-(\mathbb{E}X)^2=\frac{1-p}{p^2}\\
\dots\\
\mathbb{E}[X^2]=\frac{2-p}{p^2}=1\\
p_{1,2}=\dots[/latex]
ti imas jos -1 s lijeve strane...
razlika je sto tam suma ide od 0, ovdje ne. ipak, mislim da je to ok zbog geom. razzdiobe?
| pmli (napisa): | 4.40.
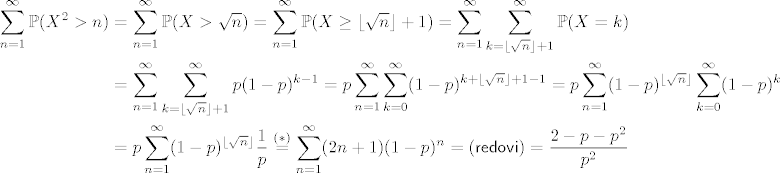
Jednakost (*) se može naslutiti iz tablice
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ... | | floor(sqrt(n)) | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 3 | 3 | ... |
|
ja sam tu isao drugom logikom, puno jednostavnije, ali nisam dobio isto rjesenje. mozes molim te naci gresku?
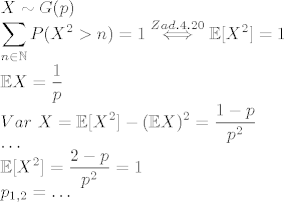
ti imas jos -1 s lijeve strane...
razlika je sto tam suma ide od 0, ovdje ne. ipak, mislim da je to ok zbog geom. razzdiobe?
_________________
...to kaj ona ima kilu viska, ja ne marim...
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
tmarusca
Forumaš(ica)


Pridružen/a: 28. 06. 2009. (20:53:52)
Postovi: (59)16
Spol: 
Lokacija: 1/039
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 23:36 ned, 26. 12. 2010 Naslov: Postano: 23:36 ned, 26. 12. 2010 Naslov: |
    |
|
|
Koristi karakterizaciju nezavisnosti sl. var. po zakonu razdiobe. Možemo uzeti da je [latex]X \sim \left(\begin{array}{ccc}
a_1 & a_2 & \ldots \\
p_1 & p_2 & \ldots
\end{array}\right)[/latex], [latex]Y \sim \left(\begin{array}{ccc}
b_1 & b_2 & \ldots \\
q_1 & q_2 & \ldots
\end{array}\right)[/latex] i [latex]Z \sim \left(\begin{array}{ccc}
c_1 & c_2 & \ldots \\
r_1 & r_2 & \ldots
\end{array}\right)[/latex]. Iskoristiš [latex]\displaystyle \{X + Y = d\} = \bigcup_i \{X = a_i, Y = d - a_i\}[/latex].
[quote="kaj"]čak i ne kužm zašto bi to trebalo biti nezavisno ?[/quote]
Sarapa je rekao za to na zadnjem predavanju da je čak, intuitivno, lako shvatiti. Kazao je nešto u stilu "ako je jedna sl. var. ne zavisi o nekim ostalima, onda sigurno ne ovisi ni o njihovom zbroju". :)
Koristi karakterizaciju nezavisnosti sl. var. po zakonu razdiobe. Možemo uzeti da je 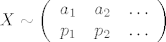 , , 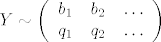 i i 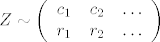 . Iskoristiš . Iskoristiš 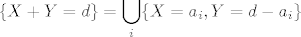 . .
| kaj (napisa): | | čak i ne kužm zašto bi to trebalo biti nezavisno ? |
Sarapa je rekao za to na zadnjem predavanju da je čak, intuitivno, lako shvatiti. Kazao je nešto u stilu "ako je jedna sl. var. ne zavisi o nekim ostalima, onda sigurno ne ovisi ni o njihovom zbroju". 
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
|



















