|
Uh, upravo sam napisao mail s tim :D
podijelimo brojnik s [latex]e^{\ arcsin x}[/latex]. To u limesu ne mijenja nista jer [latex]e^{\ arcsin x}[/latex] ide u 1.
To radimo da bismo dobili oblik e^nesto - 1 u brojniku (svodimo na poznati limes [latex]\frac{e^x-1}{x}[/latex] )
Ovo "nesto" je u nasem slucaju arctg-arcsin. Sada pomnozimo i podijelimo cijeli razlomak s tim izrazom da bismo dobili
[latex]\frac{e^{\arctan x -\arcsin x}-1}{\arctan x- \arcsin x} \frac{\arctan x- \arcsin x}{1-\cos^3 x}[/latex].
Sada znamo da ovaj prvi faktor ide u 1, pa smijemo gledati samo drugi.
Za ovaj drugi, zelimo se nekako rijesiti arctg (tj htjeli bismo sve napasti sa tangensom) pa to i radimo:
pomnozimo i podijelimo sve sa tg(brojnik)=tg(arctg-arcsin).
Sada znamo da brojnik/tg(brojnik) ide u 1 (jer brojnik ide u 0 i x/tgx -> 1 kad x-> 0) pa mozemo i to zanemariti...
Ostali smo, dakle, na [latex]\frac{\tan(\arctan x - \arcsin x)}{1-\cos^3x}[/latex].
Preostaje iskoristiti formulu za tangens razlike (pogledaj u formule ak nisi siguran) i primjetiti da se ovo u nazivniku ponasa kao x^2 do na konstantu, jer
1-cos^3=(1-cos)(cos^2+cos+1) ~ 3/2 x^2 (znamo 1-cosx ~ 1/2 x^2.)
U brojniku dobivamo (tg(arctgx)-tg(arcsin x))/ (1+tg(arctgx)tg(arcsinx)), a kad se to sredi (pomocu tgarctgx=x i tg(arcsinx)=x/cos(arcsinx))
dobivamo nesto tipa [latex]x\frac{\cos (\arcsin x)-1}{\cos(\arcsin x)+x^2}[/latex].
Sada opet koristimo [latex]\lim \frac{1-\cos(x)}{x^2}=0.5[/latex]:
vidimo da nam ovo cos(arcsinx)+x^2 ne igra previse (ide u 1)
Zato ostajemo na [latex]x \frac{\cos(\arcsin x) -1}{x^2} = \frac{\cos(\arcsin x) -1}{x} = - \frac{1- \cos(\arcsin x)}{\arcsin^2 x} \frac {\arcsin^2 x}{x^2}\frac{x^2}{x}[/latex]
Prvi faktor vidimo da ide u -1/2, drugi u 1, a treci u 0 => sve zajedno ide u 0
Sve zajedno, puno posla da bismo zakljucili da cijeli limes ide u 0.
(zapravo, jedino sto smo radili je namjestanje na poznate limese... ok, i formula za tg razlike)
@mornik: post na koji si linkao izaziva strahopostovanje :D
Uh, upravo sam napisao mail s tim 
podijelimo brojnik s 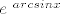 . To u limesu ne mijenja nista jer . To u limesu ne mijenja nista jer 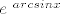 ide u 1. ide u 1.
To radimo da bismo dobili oblik e^nesto - 1 u brojniku (svodimo na poznati limes  ) )
Ovo "nesto" je u nasem slucaju arctg-arcsin. Sada pomnozimo i podijelimo cijeli razlomak s tim izrazom da bismo dobili
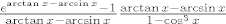 . .
Sada znamo da ovaj prvi faktor ide u 1, pa smijemo gledati samo drugi.
Za ovaj drugi, zelimo se nekako rijesiti arctg (tj htjeli bismo sve napasti sa tangensom) pa to i radimo:
pomnozimo i podijelimo sve sa tg(brojnik)=tg(arctg-arcsin).
Sada znamo da brojnik/tg(brojnik) ide u 1 (jer brojnik ide u 0 i x/tgx → 1 kad x→ 0) pa mozemo i to zanemariti...
Ostali smo, dakle, na 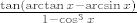 . .
Preostaje iskoristiti formulu za tangens razlike (pogledaj u formule ak nisi siguran) i primjetiti da se ovo u nazivniku ponasa kao x^2 do na konstantu, jer
1-cos^3=(1-cos)(cos^2+cos+1) ~ 3/2 x^2 (znamo 1-cosx ~ 1/2 x^2.)
U brojniku dobivamo (tg(arctgx)-tg(arcsin x))/ (1+tg(arctgx)tg(arcsinx)), a kad se to sredi (pomocu tgarctgx=x i tg(arcsinx)=x/cos(arcsinx))
dobivamo nesto tipa 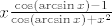 . .
Sada opet koristimo 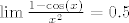 : :
vidimo da nam ovo cos(arcsinx)+x^2 ne igra previse (ide u 1)
Zato ostajemo na 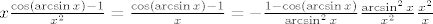
Prvi faktor vidimo da ide u -1/2, drugi u 1, a treci u 0 ⇒ sve zajedno ide u 0
Sve zajedno, puno posla da bismo zakljucili da cijeli limes ide u 0.
(zapravo, jedino sto smo radili je namjestanje na poznate limese... ok, i formula za tg razlike)
@mornik: post na koji si linkao izaziva strahopostovanje 
Zadnja promjena: pbakic; 21:21 sri, 29. 12. 2010; ukupno mijenjano 3 put/a.
|





