| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
c4rimson
Forumaš(ica)

Pridružen/a: 11. 01. 2010. (18:57:26)
Postovi: (3B)16
|
|
| [Vrh] |
|
Tangerina
Forumaš(ica)

Pridružen/a: 31. 01. 2010. (22:58:55)
Postovi: (5)16
|
|
| [Vrh] |
|
Swerz
Forumaš(ica)


Pridružen/a: 13. 02. 2009. (21:30:28)
Postovi: (182)16
Spol: 
|
 Postano: 18:58 čet, 4. 2. 2010 Naslov: Postano: 18:58 čet, 4. 2. 2010 Naslov: |
    |
|
|
1)Limes (funkcije i niza). Dokazat da je isto tj. napises obje definicije pa dokazes da imaju isti zapis (ak me kužiš)
2)Neko pitanje, odgovor je "kad je interval otvoren u širem smislu" pa to dokazati (pitanje nesto tipa niz je rastuci ali ima prekid)
3)Konvergencija, divergencija, monotonost. (pita te neko pitanje pa ti odgovoris da je monoton, pa potpitanje, pa povezujes tipa niz je monoton ali nije omedjen pa divergira pa dokazes....pa...pa....)
Uglavnom sve kaj je pitao bilo je vec negdje na forumu.
Treba sve matematicki precizno napisati. (ne iz prve jer pomaze pa ak razumijes nebus imala problema)
I da, navlaci da izvuces pozitivnu ocjenu. :wink:
Sretno svima.
1)Limes (funkcije i niza). Dokazat da je isto tj. napises obje definicije pa dokazes da imaju isti zapis (ak me kužiš)
2)Neko pitanje, odgovor je "kad je interval otvoren u širem smislu" pa to dokazati (pitanje nesto tipa niz je rastuci ali ima prekid)
3)Konvergencija, divergencija, monotonost. (pita te neko pitanje pa ti odgovoris da je monoton, pa potpitanje, pa povezujes tipa niz je monoton ali nije omedjen pa divergira pa dokazes....pa...pa....)
Uglavnom sve kaj je pitao bilo je vec negdje na forumu.
Treba sve matematicki precizno napisati. (ne iz prve jer pomaze pa ak razumijes nebus imala problema)
I da, navlaci da izvuces pozitivnu ocjenu. 
Sretno svima.
_________________
Though your dreams be tossed and blown...
|
|
| [Vrh] |
|
A_je_to
Forumaš(ica)

Pridružen/a: 19. 02. 2009. (16:51:22)
Postovi: (6D)16
Spol: 
|
|
| [Vrh] |
|
Tangerina
Forumaš(ica)

Pridružen/a: 31. 01. 2010. (22:58:55)
Postovi: (5)16
|
|
| [Vrh] |
|
kobila krsto
Forumaš(ica)
Pridružen/a: 02. 07. 2009. (16:55:08)
Postovi: (6A)16
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 12:57 sri, 5. 1. 2011 Naslov: Postano: 12:57 sri, 5. 1. 2011 Naslov: |
    |
|
|
Mislim da je "trik" u pitanju da a priori pretpostavljaš da pitanje misli na infimum u [latex]\mathbb{R}[/latex].
Npr., skup [latex]S:=\displaystyle\{\frac{\lceil10^k\sqrt{2}\rceil}{10^k}}: k\in\mathbb{N}\}[/latex] je odozdo omeđen i vrijedi [latex]S\subseteq\mathbb{Q}(\subseteq\mathbb{R})[/latex]. No, skup [latex]S[/latex] nema infimum u [latex]\mathbb{Q}[/latex]. Naravno, on u [latex]\mathbb{R}[/latex] ima infimum: to je upravo [latex]\sqrt{2}[/latex].
(Mogao sam naći i lakši primjer, ali ovaj mi je prvi pao na pamet. :D)
A15 (ili neka njegova ekvivalencija, ovisi kako se postavi) kaže da svaki odozdo omeđen neprazan skup [latex]S\subseteq\mathbb{R}[/latex] ima infimum u skupu realnih brojeva i u njemu je odgovor na tvoje pitanje, ako ja nešto nisam previdio, da. No, ta tvrdnja ne vrijedi nužno za ostale (linearno uređene, kako tvoje pitanje kaže) skupove, kao što se gore vidi.
Mislim da je "trik" u pitanju da a priori pretpostavljaš da pitanje misli na infimum u  . .
Npr., skup 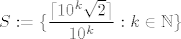 je odozdo omeđen i vrijedi je odozdo omeđen i vrijedi 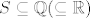 . No, skup . No, skup  nema infimum u nema infimum u 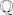 . Naravno, on u . Naravno, on u  ima infimum: to je upravo ima infimum: to je upravo 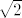 . .
(Mogao sam naći i lakši primjer, ali ovaj mi je prvi pao na pamet.  ) )
A15 (ili neka njegova ekvivalencija, ovisi kako se postavi) kaže da svaki odozdo omeđen neprazan skup  ima infimum u skupu realnih brojeva i u njemu je odgovor na tvoje pitanje, ako ja nešto nisam previdio, da. No, ta tvrdnja ne vrijedi nužno za ostale (linearno uređene, kako tvoje pitanje kaže) skupove, kao što se gore vidi. ima infimum u skupu realnih brojeva i u njemu je odgovor na tvoje pitanje, ako ja nešto nisam previdio, da. No, ta tvrdnja ne vrijedi nužno za ostale (linearno uređene, kako tvoje pitanje kaže) skupove, kao što se gore vidi.
|
|
| [Vrh] |
|
Togepi
Forumaš(ica)
Pridružen/a: 21. 11. 2010. (14:31:41)
Postovi: (2B)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 15:01 sri, 5. 1. 2011 Naslov: Postano: 15:01 sri, 5. 1. 2011 Naslov: |
    |
|
|
Pogledaj u [url=http://web.math.hr/~guljas/skripte/MATANALuR.pdf]skriptu[/url], str. 74 za sinus, a str. 78 za arkus sinusa (u smislu Teorema 3.14. promatramo [latex]\displaystyle\sin\mid_{[-\frac{\pi}{2},\frac{\pi}{2}]}:[-\frac{\pi}{2},\frac{\pi}{2}]\to[-1,1][/latex], u kojem slučaju možemo reći da je ta funkcija bijekcija).
EDIT: Imaš još i na str. 81 baš dokaz za arkus funkcije.
Pogledaj u skriptu, str. 74 za sinus, a str. 78 za arkus sinusa (u smislu Teorema 3.14. promatramo 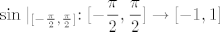 , u kojem slučaju možemo reći da je ta funkcija bijekcija). , u kojem slučaju možemo reći da je ta funkcija bijekcija).
EDIT: Imaš još i na str. 81 baš dokaz za arkus funkcije.
Zadnja promjena: mornik; 19:51 sri, 5. 1. 2011; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
 Postano: 19:45 čet, 6. 1. 2011 Naslov: Postano: 19:45 čet, 6. 1. 2011 Naslov: |
    |
|
|
Treba dokazati da je svaki podniz odozgo ograničenog niza i sam odozgo ograničen, ne znam niti kako bih počela formalni dokaz pa može dokaz,hint,nešto ? :D
Usput, ako tko ima volje da pojasni zašto je (A15) ekvivalent Cantorovog i Arhimedovog aksioma, gdje smo dokazali jedan smjer i kako drugi?
Hvala :D
Treba dokazati da je svaki podniz odozgo ograničenog niza i sam odozgo ograničen, ne znam niti kako bih počela formalni dokaz pa može dokaz,hint,nešto ? 
Usput, ako tko ima volje da pojasni zašto je (A15) ekvivalent Cantorovog i Arhimedovog aksioma, gdje smo dokazali jedan smjer i kako drugi?
Hvala 
|
|
| [Vrh] |
|
Boris B.
Forumaš(ica)

Pridružen/a: 19. 01. 2010. (18:01:54)
Postovi: (32)16
Spol: 
|
 Postano: 20:08 čet, 6. 1. 2011 Naslov: Postano: 20:08 čet, 6. 1. 2011 Naslov: |
    |
|
|
[quote="pupi"]Treba dokazati da je svaki podniz odozgo ograničenog niza i sam odozgo ograničen, ne znam niti kako bih počela formalni dokaz pa može dokaz,hint,nešto ? :D
Usput, ako tko ima volje da pojasni zašto je (A15) ekvivalent Cantorovog i Arhimedovog aksioma, gdje smo dokazali jedan smjer i kako drugi?
Hvala :D[/quote]
Pošto vrijedi i u Q, Arhimedov aksiom [i]nije[/i] ekvivalentan s potpunošću, tj. s aksiomom A15.
Ovo prvo slijedi iz definicije podniza i ograničenosti:
Niz je ograničen ako postoji realan A td. je za sve n iz N a(n) <= A. (1)
Ali ako je b podniz niza a, tada postoji strogo rastuća funkcija p: N -> N, td. je za sve n b(n) = a(p(n)). No kako je p(n) prirodan broj, onda je po (1) a(p(n)) <= A.
Dakle, za sve prirodne n je b(n) <= A, pa je b ograničen.
| pupi (napisa): | Treba dokazati da je svaki podniz odozgo ograničenog niza i sam odozgo ograničen, ne znam niti kako bih počela formalni dokaz pa može dokaz,hint,nešto ? 
Usput, ako tko ima volje da pojasni zašto je (A15) ekvivalent Cantorovog i Arhimedovog aksioma, gdje smo dokazali jedan smjer i kako drugi?
Hvala  |
Pošto vrijedi i u Q, Arhimedov aksiom nije ekvivalentan s potpunošću, tj. s aksiomom A15.
Ovo prvo slijedi iz definicije podniza i ograničenosti:
Niz je ograničen ako postoji realan A td. je za sve n iz N a(n) ⇐ A. (1)
Ali ako je b podniz niza a, tada postoji strogo rastuća funkcija p: N → N, td. je za sve n b(n) = a(p(n)). No kako je p(n) prirodan broj, onda je po (1) a(p(n)) ⇐ A.
Dakle, za sve prirodne n je b(n) ⇐ A, pa je b ograničen.
_________________
The lyf so short, the craft so long to lerne
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
 Postano: 20:11 čet, 6. 1. 2011 Naslov: Postano: 20:11 čet, 6. 1. 2011 Naslov: |
    |
|
|
[quote="Boris B."][quote="pupi"]Treba dokazati da je svaki podniz odozgo ograničenog niza i sam odozgo ograničen, ne znam niti kako bih počela formalni dokaz pa može dokaz,hint,nešto ? :D
Usput, ako tko ima volje da pojasni zašto je (A15) ekvivalent Cantorovog i Arhimedovog aksioma, gdje smo dokazali jedan smjer i kako drugi?
Hvala :D[/quote]
Pošto vrijedi i u Q, Arhimedov aksiom [i]nije[/i] ekvivalentan s potpunošću, tj. s aksiomom A15.[/quote]
Ne Arhimedov aksiom nego kombinacija Cantorovog i Arhimedovog :)
[quote="Boris B."]Ovo prvo slijedi iz definicije podniza i ograničenosti:
Niz je ograničen ako postoji realan A td. je za sve n iz N a(n) <= A. (1)
Ali ako je b podniz niza a, tada postoji strogo rastuća funkcija p: N -> N, td. je za sve n b(n) = a(p(n)). No kako je p(n) prirodan broj, onda je po (1) a(p(n)) <= A.
Dakle, za sve prirodne n je b(n) < A, pa je b ograničen.[/quote]Tnx
| Boris B. (napisa): | | pupi (napisa): | Treba dokazati da je svaki podniz odozgo ograničenog niza i sam odozgo ograničen, ne znam niti kako bih počela formalni dokaz pa može dokaz,hint,nešto ? 
Usput, ako tko ima volje da pojasni zašto je (A15) ekvivalent Cantorovog i Arhimedovog aksioma, gdje smo dokazali jedan smjer i kako drugi?
Hvala  |
Pošto vrijedi i u Q, Arhimedov aksiom nije ekvivalentan s potpunošću, tj. s aksiomom A15. |
Ne Arhimedov aksiom nego kombinacija Cantorovog i Arhimedovog 
| Boris B. (napisa): | Ovo prvo slijedi iz definicije podniza i ograničenosti:
Niz je ograničen ako postoji realan A td. je za sve n iz N a(n) ⇐ A. (1)
Ali ako je b podniz niza a, tada postoji strogo rastuća funkcija p: N → N, td. je za sve n b(n) = a(p(n)). No kako je p(n) prirodan broj, onda je po (1) a(p(n)) ⇐ A.
Dakle, za sve prirodne n je b(n) < A, pa je b ograničen. |
Tnx
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 21:50 čet, 6. 1. 2011 Naslov: Postano: 21:50 čet, 6. 1. 2011 Naslov: |
    |
|
|
Ajde, prvo me čovjek pita mailom, onda me dvojica pitaju PM-om... tako da sad već imam spreman odgovor. :D
So, lo and behold, dokaz (i objašnjenje meni pomalo nejasnog dijela) "drugog" smjera ekvivalencije (Cantorov aksiom ste dokazivali iz ovih 15 aksioma na satu, jel tako? :D). Isti je u formi svojedobnog maila kojim sam odgovorio prvom čovjeku koji me pitao, pomalo izmijenjen zbog tipfelera, nekih mojih komentara i LaTeXiranja, ali izuzev toga jednak. Stoga, ovaj post možda zvuči malo čudno (kompilacija maila i PM-ova :D). :) Kao što piše u mailu, možda se treba malo potruditi da se shvati iz iskaza i dokaza da se zapravo dokazuje A15 putem Cantorovog aksioma (u ovom tekstu referiranog kao "nested interval principle"), ali to je to.
[quote="svojedobni mail"]
Evo, pogledaj stranicu 98 u ovoj knjizi: http://books.google.com/books?id=YSe4hUBM7uEC [i][ima preview gumb negdje; nadam se da se, i godinu poslije, još uvijek radi o stranici 98, a čini mi se da da][/i].
Tu se nalazi više-manje sve što te zanima (ne piše tim riječima, ali teorem pretpostavlja Cantorov aksiom i pomoću njega dokazuje A15), jedino je na jednom mjestu autor neprecizan pa ne koristi Arhimedov aksiom (makar, primijetit ćemo da Arhimedov aksiom, što i kaže prof. Guljaš u svojoj skripti: http://web.math.hr/~guljas/skripte/MATANALuR.pdf, već slijedi iz A1-A14, tako da njega ionako ne trebamo posebno navoditi). To je na mjestu gdje zaključi da za svaki [latex]L<c[/latex] možemo naći [latex]x_k[/latex] takav da je [latex]L<x_k<c[/latex]. (Analogno za [latex]M[/latex].)
To ću sada (probati, čista aksiomatika mi i nije najdraža stvar...) razjasniti pomoću Arhimedovog aksioma, a ti reci ako ti i neki drugi dio nije najjasniji. Dakle, budući da je [latex]y_k-x_k=\displaystyle\frac{y_1-x_1}{2^{k-1}}[/latex], a [latex]c[/latex] je unutar svakog [latex][x_k,y_k][/latex], vrijedi da je [latex]0\leq c-x_k\leq\displaystyle\frac{y_1-x_1}{2^k}[/latex]. Sad još samo treba dokazati da [latex]c-x_k[/latex] ide u [latex]0[/latex]: onda ću moći za svaki [latex]L[/latex] i [latex]c[/latex], [latex]L<c[/latex], uzeti neki [latex]x_k[/latex] između njih... raspiši si ako ima problema - naprosto uzmem [latex]0<\epsilon<L-c[/latex], a onda iz toga da [latex]c-x_k[/latex] ide u [latex]0[/latex] ću znati da imam [latex]x_k[/latex] takav da je [latex]0<c-x_k<\epsilon<L-c[/latex].
I sad još preostaje pokazati da [latex]c-x_k[/latex] ide u [latex]0[/latex]. Naravno, dovoljno je da dokažem (teorem o sendviču i dalje "radi" :)) da [latex]\displaystyle\frac{y_1-x_1}{2^k}[/latex] ide u [latex]0[/latex] za [latex]k[/latex] koji ide u [latex]+\infty[/latex]. A to ćemo dokazati po definiciji: neka je [latex]t>0[/latex] ([latex]t[/latex] mi igra ulogu epsilona). Tada želim dokazati da nakon konačno mnogo [latex]k[/latex] imamo [latex]\displaystyle\frac{y_1-x_1}{2^k}<t[/latex] , tj. [latex]\displaystyle\frac{1}{2^k}<\frac{t}{y_1-x_1}[/latex]. [i][U originalu su mi brojnik i nazivnik u razlomku zdesna bili zamijenjeni, ali to mi se čini da je tipfeler, ne? Ukratko, ako se ovo čini krivo, probaj tu i dalje zamijeniti odgovarajući brojnik i nazivnik. :D][/i] Sad, ja mogu indukcijom ili čime već dokazati da vrijedi [latex]2^k\geq k[/latex], pa mi je dovoljno dokazati da nakon konačno mnogo [latex]k[/latex] vrijedi [latex]\displaystyle\frac{1}{k}<\frac{t}{y_1-x_1}[/latex], a to je naprosto Arhimedov aksiom: postoji [latex]k_0[/latex] iz [latex]\mathbb{N}[/latex] takav da vrijedi [latex]\displaystyle k_0\frac{t}{y_1-x_1}>1[/latex] , a onda za sve [latex]k\geq k_0[/latex] i dalje to vrijedi, pa smo gotovi.
Evo, probao sam u kratkim crtama izložiti o čemu se radi, kažem, glavni dio možeš pronaći na linku koji sam ti poslao, a onda pitaj ako nešto nije jasno.
[/quote]
Evo, pitaj ako nešto ne bude jasno (sasvim je moguće da gore imam nekih nenamjernih grešaka koje su nastale LaTeXiranjem), pa ćemo prodiskutirati. :D Nisam se sad ponovno udubljivao u taj dokaz, tako da je moguće da ima takvih nenamjernih grešaka - kao što rekoh, glavni dio dokaza je na ovom linku gore, ovo je samo neko moje objašnjenje dijela koji mi se čini malo mutniji. :D
Ajde, prvo me čovjek pita mailom, onda me dvojica pitaju PM-om... tako da sad već imam spreman odgovor. 
So, lo and behold, dokaz (i objašnjenje meni pomalo nejasnog dijela) "drugog" smjera ekvivalencije (Cantorov aksiom ste dokazivali iz ovih 15 aksioma na satu, jel tako?  ). Isti je u formi svojedobnog maila kojim sam odgovorio prvom čovjeku koji me pitao, pomalo izmijenjen zbog tipfelera, nekih mojih komentara i LaTeXiranja, ali izuzev toga jednak. Stoga, ovaj post možda zvuči malo čudno (kompilacija maila i PM-ova ). Isti je u formi svojedobnog maila kojim sam odgovorio prvom čovjeku koji me pitao, pomalo izmijenjen zbog tipfelera, nekih mojih komentara i LaTeXiranja, ali izuzev toga jednak. Stoga, ovaj post možda zvuči malo čudno (kompilacija maila i PM-ova  ). ).  Kao što piše u mailu, možda se treba malo potruditi da se shvati iz iskaza i dokaza da se zapravo dokazuje A15 putem Cantorovog aksioma (u ovom tekstu referiranog kao "nested interval principle"), ali to je to. Kao što piše u mailu, možda se treba malo potruditi da se shvati iz iskaza i dokaza da se zapravo dokazuje A15 putem Cantorovog aksioma (u ovom tekstu referiranog kao "nested interval principle"), ali to je to.
| svojedobni mail (napisa): |
Evo, pogledaj stranicu 98 u ovoj knjizi: http://books.google.com/books?id=YSe4hUBM7uEC [ima preview gumb negdje; nadam se da se, i godinu poslije, još uvijek radi o stranici 98, a čini mi se da da].
Tu se nalazi više-manje sve što te zanima (ne piše tim riječima, ali teorem pretpostavlja Cantorov aksiom i pomoću njega dokazuje A15), jedino je na jednom mjestu autor neprecizan pa ne koristi Arhimedov aksiom (makar, primijetit ćemo da Arhimedov aksiom, što i kaže prof. Guljaš u svojoj skripti: http://web.math.hr/~guljas/skripte/MATANALuR.pdf, već slijedi iz A1-A14, tako da njega ionako ne trebamo posebno navoditi). To je na mjestu gdje zaključi da za svaki 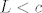 možemo naći možemo naći 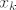 takav da je takav da je 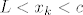 . (Analogno za . (Analogno za  .) .)
To ću sada (probati, čista aksiomatika mi i nije najdraža stvar...) razjasniti pomoću Arhimedovog aksioma, a ti reci ako ti i neki drugi dio nije najjasniji. Dakle, budući da je 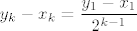 , a , a  je unutar svakog je unutar svakog 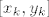 , vrijedi da je , vrijedi da je 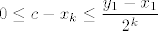 . Sad još samo treba dokazati da . Sad još samo treba dokazati da 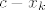 ide u ide u  : onda ću moći za svaki : onda ću moći za svaki  i i  , , 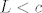 , uzeti neki , uzeti neki 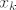 između njih... raspiši si ako ima problema - naprosto uzmem između njih... raspiši si ako ima problema - naprosto uzmem 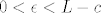 , a onda iz toga da , a onda iz toga da 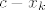 ide u ide u  ću znati da imam ću znati da imam 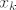 takav da je takav da je  . .
I sad još preostaje pokazati da 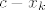 ide u ide u  . Naravno, dovoljno je da dokažem (teorem o sendviču i dalje "radi" . Naravno, dovoljno je da dokažem (teorem o sendviču i dalje "radi"  ) da ) da 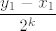 ide u ide u  za za  koji ide u koji ide u  . A to ćemo dokazati po definiciji: neka je . A to ćemo dokazati po definiciji: neka je 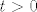 ( ( mi igra ulogu epsilona). Tada želim dokazati da nakon konačno mnogo mi igra ulogu epsilona). Tada želim dokazati da nakon konačno mnogo  imamo imamo 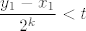 , tj. , tj. 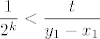 . [U originalu su mi brojnik i nazivnik u razlomku zdesna bili zamijenjeni, ali to mi se čini da je tipfeler, ne? Ukratko, ako se ovo čini krivo, probaj tu i dalje zamijeniti odgovarajući brojnik i nazivnik. . [U originalu su mi brojnik i nazivnik u razlomku zdesna bili zamijenjeni, ali to mi se čini da je tipfeler, ne? Ukratko, ako se ovo čini krivo, probaj tu i dalje zamijeniti odgovarajući brojnik i nazivnik.  ] Sad, ja mogu indukcijom ili čime već dokazati da vrijedi ] Sad, ja mogu indukcijom ili čime već dokazati da vrijedi  , pa mi je dovoljno dokazati da nakon konačno mnogo , pa mi je dovoljno dokazati da nakon konačno mnogo  vrijedi vrijedi 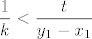 , a to je naprosto Arhimedov aksiom: postoji , a to je naprosto Arhimedov aksiom: postoji 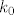 iz iz 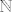 takav da vrijedi takav da vrijedi 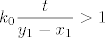 , a onda za sve , a onda za sve  i dalje to vrijedi, pa smo gotovi. i dalje to vrijedi, pa smo gotovi.
Evo, probao sam u kratkim crtama izložiti o čemu se radi, kažem, glavni dio možeš pronaći na linku koji sam ti poslao, a onda pitaj ako nešto nije jasno.
|
Evo, pitaj ako nešto ne bude jasno (sasvim je moguće da gore imam nekih nenamjernih grešaka koje su nastale LaTeXiranjem), pa ćemo prodiskutirati.  Nisam se sad ponovno udubljivao u taj dokaz, tako da je moguće da ima takvih nenamjernih grešaka - kao što rekoh, glavni dio dokaza je na ovom linku gore, ovo je samo neko moje objašnjenje dijela koji mi se čini malo mutniji. Nisam se sad ponovno udubljivao u taj dokaz, tako da je moguće da ima takvih nenamjernih grešaka - kao što rekoh, glavni dio dokaza je na ovom linku gore, ovo je samo neko moje objašnjenje dijela koji mi se čini malo mutniji. 
|
|
| [Vrh] |
|
kre5o
Forumaš(ica)
Pridružen/a: 14. 09. 2009. (22:20:52)
Postovi: (32)16
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 15:37 pet, 14. 1. 2011 Naslov: Postano: 15:37 pet, 14. 1. 2011 Naslov: |
    |
|
|
Usmeni je ponedjeljkom, utorkom i srijedom od 8 do 12 sati. Dakle, svaki dan su 4 grupe i 4 studenta (iznimka je posljednja grupa, u toj grupi ih je 5). Studenti su poredani abecedno, što znači da je "granica" između ponedjeljka i utorka negdje oko slova N ili O, a "granica" između utorka i srijede slovo S (prva tri studenta na S odgovaraju u utorak, a ostali su u srijedu).
Ne bih ti mogao reći više od toga. Ako je tvoje prezime otprilike u skupini koju sam otprilike upamtio, možda bih ti mogao čak i "predvidjeti" termin. Najbolje ti je da, ako nemaš usmeni u srijedu, da odeš do faksa vidjeti u koliko si točno sati.
Zapravo, kad malo bolje razmislim: ako s Interneta kopiraš tablicu s rezultatima u Excel i izbaciš sve studente od A-Lj te one koji imaju manje ili jednako 25 bodova i ostaviš je poredanu po abecedi, dobit ćeš vrlo vjerodostojan redoslijed ispitivanja. Dakle, računaš si grupe po 4 studenta i možeš otprilike odrediti kada odgovaraš.
Samo, moram se ispraviti: čini se da samo 3 grupe odgovaraju analizu u ponedjeljak, i to od 8 do 11. Tako mi se čini prema tablici koju sam si izradio.
U svakom slučaju, nije loše provjeriti popis na faksu ako slučajno postoji kakva iznimka od ovoga "pravila". Ali barem otprilike možeš znati kada si na redu.
Usmeni je ponedjeljkom, utorkom i srijedom od 8 do 12 sati. Dakle, svaki dan su 4 grupe i 4 studenta (iznimka je posljednja grupa, u toj grupi ih je 5). Studenti su poredani abecedno, što znači da je "granica" između ponedjeljka i utorka negdje oko slova N ili O, a "granica" između utorka i srijede slovo S (prva tri studenta na S odgovaraju u utorak, a ostali su u srijedu).
Ne bih ti mogao reći više od toga. Ako je tvoje prezime otprilike u skupini koju sam otprilike upamtio, možda bih ti mogao čak i "predvidjeti" termin. Najbolje ti je da, ako nemaš usmeni u srijedu, da odeš do faksa vidjeti u koliko si točno sati.
Zapravo, kad malo bolje razmislim: ako s Interneta kopiraš tablicu s rezultatima u Excel i izbaciš sve studente od A-Lj te one koji imaju manje ili jednako 25 bodova i ostaviš je poredanu po abecedi, dobit ćeš vrlo vjerodostojan redoslijed ispitivanja. Dakle, računaš si grupe po 4 studenta i možeš otprilike odrediti kada odgovaraš.
Samo, moram se ispraviti: čini se da samo 3 grupe odgovaraju analizu u ponedjeljak, i to od 8 do 11. Tako mi se čini prema tablici koju sam si izradio.
U svakom slučaju, nije loše provjeriti popis na faksu ako slučajno postoji kakva iznimka od ovoga "pravila". Ali barem otprilike možeš znati kada si na redu.
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 18:05 sub, 15. 1. 2011 Naslov: Postano: 18:05 sub, 15. 1. 2011 Naslov: |
    |
|
|
Možda bi bilo korisno da pojasniš malo o kojem se kontekstu radi. :D
Ovako generalno gledano, koliko ja vidim, ova zadnja rečenica je netočna negacija definicije konvergencije niza: [latex](\exists L\in\mathbb{R})(\forall \varepsilon>0)(\exists m\in\mathbb{N})(\forall n\in\mathbb{N})(n\geq m\Rightarrow |a_n-L|\leq \varepsilon)[/latex]. Kad to negiramo, dobivamo [latex](\forall L\in\mathbb{R})(\exists \varepsilon>0)(\forall m\in\mathbb{N})(\exists n\in\mathbb{N})(n\geq m \wedge |a_n-L|\geq \varepsilon)[/latex].
E, sad, ovo da [latex]\varepsilon[/latex] može ovisiti o [latex]L[/latex] (i slična stvar za [latex]n[/latex]) - to se stavlja samo kao pojašnjenje da [latex]\varepsilon[/latex] nije nužno isti za svaki [latex]L[/latex]. Naime, razmisli o logici ovoga - za jedan [latex]L[/latex] ti možeš pronaći jedan [latex]\varepsilon[/latex] za koji vrijedi nastavak te izjave, dok je za drugi [latex]L[/latex] primjereni [latex]\varepsilon[/latex] eventualno drugačiji - nemaš nikakvih ograničenja da oni moraju biti isti. Stoga, [latex]\varepsilon[/latex] zapravo ovisi o [latex]L[/latex] (mislim, on ne mora ovisiti, može i uvijek isti kontraprimjer djelovati... ali može). Tako ideš i dalje: našli smo, dakle, [latex]\varepsilon[/latex]. Sad, za svaki [latex]m[/latex] mi moramo pronaći [latex]n[/latex] takav da ovo tu vrijedi. Ponovno, taj [latex]n[/latex] ovisi o [latex]m[/latex] (npr. mora biti veći ili jednak [latex]m[/latex]), a ovisi i o epsilonu - on ne mora biti jednak za sve epsilone ili za sve [latex]m[/latex].
Ne znam sad koliko sam uspješno objasnio, ali poanta je da samo naglašavamo da nam je izbor epsilona i [latex]n[/latex] "slobodan" - nije isti za svaki [latex]L[/latex] ili [latex]m[/latex]. Objašnjenje je zapravo posve isto kao kad u gore napisanoj definiciji konvergencije pišete [latex][\ldots](\exists m=m(\varepsilon)\in\mathbb{N})[\ldots][/latex], što ste sigurno radili - dakle, [latex]m[/latex] tu nije nužno isti za svaki epsilon.
EDIT: Glup i ružan tipfeler. :oops:
Možda bi bilo korisno da pojasniš malo o kojem se kontekstu radi. 
Ovako generalno gledano, koliko ja vidim, ova zadnja rečenica je netočna negacija definicije konvergencije niza: 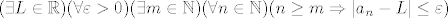 . Kad to negiramo, dobivamo . Kad to negiramo, dobivamo 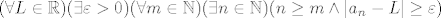 . .
E, sad, ovo da  može ovisiti o može ovisiti o  (i slična stvar za (i slična stvar za  ) - to se stavlja samo kao pojašnjenje da ) - to se stavlja samo kao pojašnjenje da  nije nužno isti za svaki nije nužno isti za svaki  . Naime, razmisli o logici ovoga - za jedan . Naime, razmisli o logici ovoga - za jedan  ti možeš pronaći jedan ti možeš pronaći jedan  za koji vrijedi nastavak te izjave, dok je za drugi za koji vrijedi nastavak te izjave, dok je za drugi  primjereni primjereni  eventualno drugačiji - nemaš nikakvih ograničenja da oni moraju biti isti. Stoga, eventualno drugačiji - nemaš nikakvih ograničenja da oni moraju biti isti. Stoga,  zapravo ovisi o zapravo ovisi o  (mislim, on ne mora ovisiti, može i uvijek isti kontraprimjer djelovati... ali može). Tako ideš i dalje: našli smo, dakle, (mislim, on ne mora ovisiti, može i uvijek isti kontraprimjer djelovati... ali može). Tako ideš i dalje: našli smo, dakle,  . Sad, za svaki . Sad, za svaki  mi moramo pronaći mi moramo pronaći  takav da ovo tu vrijedi. Ponovno, taj takav da ovo tu vrijedi. Ponovno, taj  ovisi o ovisi o  (npr. mora biti veći ili jednak (npr. mora biti veći ili jednak  ), a ovisi i o epsilonu - on ne mora biti jednak za sve epsilone ili za sve ), a ovisi i o epsilonu - on ne mora biti jednak za sve epsilone ili za sve  . .
Ne znam sad koliko sam uspješno objasnio, ali poanta je da samo naglašavamo da nam je izbor epsilona i  "slobodan" - nije isti za svaki "slobodan" - nije isti za svaki  ili ili  . Objašnjenje je zapravo posve isto kao kad u gore napisanoj definiciji konvergencije pišete . Objašnjenje je zapravo posve isto kao kad u gore napisanoj definiciji konvergencije pišete 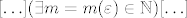 , što ste sigurno radili - dakle, , što ste sigurno radili - dakle,  tu nije nužno isti za svaki epsilon. tu nije nužno isti za svaki epsilon.
EDIT: Glup i ružan tipfeler. 
Zadnja promjena: mornik; 9:04 ned, 16. 1. 2011; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
|












