| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 21:37 sri, 5. 1. 2011 Naslov: Postano: 21:37 sri, 5. 1. 2011 Naslov: |
    |
|
|
3. [latex]Df(c_1, c_2)(x, y) = (A | x) c_2 + (A | c_1) y + 2 (c_2 | y) c_1 + \| c_2 \|^2 x[/latex], [latex]Df(x, A)(x, A) = (A | x) A + (A | x) A + 2 (A | A) x + \| A \|^2 x = 2 a^2 (4 x_1 + x_2, x_1 + 4 x_2)[/latex]
6.
[latex]\displaystyle $\begin{align} Df(x)(a) & = \frac{1}{1 + \| x \|^4} \cdot 2 (x | a) x + \arctan \| x \|^2 a \\ & = \left( \frac{n (n + 1)}{n^2 + 1} + \arctan n, \frac{n (n + 1)}{n^2 + 1} + 2 \arctan n, \ldots, \frac{n (n + 1)}{n^2 + 1} + n \arctan n \right)\end{align}$[/latex]
Kod ovakvih zadataka za provjeru možeš koristiti Mathematicu (a valjda i WolframAlphu). Jacobijeva matrica se dobiva funkcijom D, npr. za fju 3 varijable treba staviti [code:1]D[f[x, y, z], {{x, y, z}}][/code:1]
Operator za skalarni produkt i množenje matrica je točka.
3. 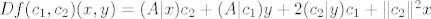 , , 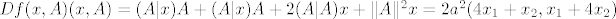
6.
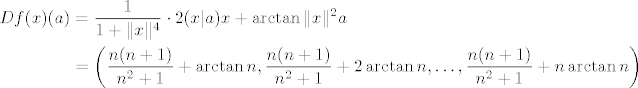
Kod ovakvih zadataka za provjeru možeš koristiti Mathematicu (a valjda i WolframAlphu). Jacobijeva matrica se dobiva funkcijom D, npr. za fju 3 varijable treba staviti | Kod: | | D[f[x, y, z], {{x, y, z}}] |
Operator za skalarni produkt i množenje matrica je točka.
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 14:16 čet, 6. 1. 2011 Naslov: Postano: 14:16 čet, 6. 1. 2011 Naslov: |
    |
|
|
Prvo izracunamo tocku u kojoj trazimo tangencijalnu ravninu:
[latex]M(u_0,v_0)[/latex] valjda znaci [latex]\Phi(u_0,v_0)[/latex]
Sada imamo
[latex]\cos(u_0)=\frac{3}{5}[/latex], ali ova restrikcija [latex]u_0>0[/latex] nam ne govori puno (moguce su dvije takve tocke), pa pretp. [latex]\sin(u_0)=\frac{4}{5}[/latex]
[latex]\cos(v_0)=\frac{4}{5}[/latex] i [latex]v_0<\frac{\pi}{2} \Rightarrow \sin{v_0}=\frac{3}{5}[/latex]
Kad to uvrstimo, dobijemo [latex]\Phi(u_0,v_0)=(\frac{16}{5},\frac{12}{5},4)[/latex]
Sada znamo da jednadzba tg. ravnine izgleda ovako:
[latex]A(x-\frac{16}{5})+B(y-\frac{12}{5})+C(z-4)=0[/latex]
gdje je (A,B,C) neki vektor normale tangencijalne ravnine.
Vektor normale dobijemo tako da nadjemo dva tangencijalna vektora i pomnozimo ih vektorski.
Tangencijalne vektore nadjemo tako da racunamo
[latex]\frac{d\Phi}{du}[/latex] i [latex]\frac{d\Phi}{dv}[/latex] u tocki [latex](u_0,v_0)[/latex]
Ako oznacimo [latex]\Phi=(f_1,f_2,f_3)[/latex], onda vrijedi
[latex]\frac{d\Phi}{du}=(\frac{df_1}{du},\frac{df_2}{du},\frac{df_3}{du})[/latex] i
[latex]\frac{d\Phi}{dv}=(\frac{df_1}{dv},\frac{df_2}{dv},\frac{df_3}{dv})[/latex]
Sad nadjemo ta dva vektora u tocki [latex](u_0,v_0)[/latex], pomnozimo ih vektorski (determinanta), i time dobijemo trazeni vektor normale.
Prvo izracunamo tocku u kojoj trazimo tangencijalnu ravninu:
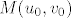 valjda znaci valjda znaci 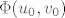
Sada imamo
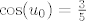 , ali ova restrikcija , ali ova restrikcija  nam ne govori puno (moguce su dvije takve tocke), pa pretp. nam ne govori puno (moguce su dvije takve tocke), pa pretp. 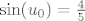
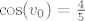 i i 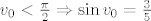
Kad to uvrstimo, dobijemo 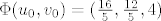
Sada znamo da jednadzba tg. ravnine izgleda ovako:
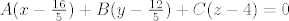
gdje je (A,B,C) neki vektor normale tangencijalne ravnine.
Vektor normale dobijemo tako da nadjemo dva tangencijalna vektora i pomnozimo ih vektorski.
Tangencijalne vektore nadjemo tako da racunamo
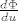 i i 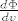 u tocki u tocki 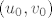
Ako oznacimo 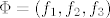 , onda vrijedi , onda vrijedi
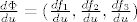 i i
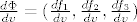
Sad nadjemo ta dva vektora u tocki 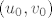 , pomnozimo ih vektorski (determinanta), i time dobijemo trazeni vektor normale. , pomnozimo ih vektorski (determinanta), i time dobijemo trazeni vektor normale.
|
|
| [Vrh] |
|
šišmiš
Forumaš(ica)

Pridružen/a: 19. 04. 2010. (21:01:19)
Postovi: (29)16
|
|
| [Vrh] |
|
|







