| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ceps
Forumaš(ica)
Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 15:17 čet, 6. 1. 2011 Naslov: Jedan zadatak sa supremumima i infimumima... |
    |
|
|
Odredite, ako postoje sup i inf skupa:
[latex]S := \{ log_2 \frac{10mn}{(2m + 5n)^2}: m, n \in N \} [/latex]
E sad, ovaj [latex]log_2[/latex] mi ne smeta jer je rastuća funkcija, pa je bitno samo promatrati ovaj dio ''unutra'', nazovimo ga T - pa će sup S biti log sup T, tako i za infimum.
Taj dio unutra mogu rastaviti kao: [latex]\frac{2m}{2m + 5n} \cdot \frac{5n}{2m + 5n}[/latex], ali ne znam što bi dalje sa tim dijelovima... Mislim, rezultati moraju biti u intervalu između 0 i 1, ali kako pokazati da su to zbilja infimum i supremum, ako uopće jesu? Sigurno je nešto očito na što sam zaboravio, možda sam već i previše stvari napravio danas pa sam malo umoran, ali ovaj zadatak me sad jako živcira :evil: , pa ako može kakav hintić. :lol:
Odredite, ako postoje sup i inf skupa:
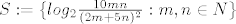
E sad, ovaj 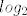 mi ne smeta jer je rastuća funkcija, pa je bitno samo promatrati ovaj dio ''unutra'', nazovimo ga T - pa će sup S biti log sup T, tako i za infimum.
Taj dio unutra mogu rastaviti kao: 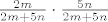 , ali ne znam što bi dalje sa tim dijelovima... Mislim, rezultati moraju biti u intervalu između 0 i 1, ali kako pokazati da su to zbilja infimum i supremum, ako uopće jesu? Sigurno je nešto očito na što sam zaboravio, možda sam već i previše stvari napravio danas pa sam malo umoran, ali ovaj zadatak me sad jako živcira  , pa ako može kakav hintić. 
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)
Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)
Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)
Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol:
|
| Postano: 17:29 čet, 6. 1. 2011 Naslov: |
|
|
|
Homogeno ovdje znaci da je svaki dio izraza istog stupnja:
razlomak je: 10mn/(4m^2+20mn+25n^2)
U brojiniku imas mn (stupnja 2)
U nazivniku m^2, n^2 i mn, takodjer sve stupnja 2.
Kad bi bio neki izraz tipa (m^2+n^2)/(m^2+n), ne bi mogli ovo napraviti jer bi se u nazivniku pojavio n/m^2. Kako zelimo supstituirati q=n/m, ovo nam ne bi pasalo.
Btw, nisam ipak tolko stariji :P
Homogeno ovdje znaci da je svaki dio izraza istog stupnja:
razlomak je: 10mn/(4m^2+20mn+25n^2)
U brojiniku imas mn (stupnja 2)
U nazivniku m^2, n^2 i mn, takodjer sve stupnja 2.
Kad bi bio neki izraz tipa (m^2+n^2)/(m^2+n), ne bi mogli ovo napraviti jer bi se u nazivniku pojavio n/m^2. Kako zelimo supstituirati q=n/m, ovo nam ne bi pasalo.
Btw, nisam ipak tolko stariji 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)
Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
| Postano: 17:44 čet, 6. 1. 2011 Naslov: |
|
|
|
[quote="pbakic"]Homogeno ovdje znaci da je svaki dio izraza istog stupnja:
razlomak je: 10mn/(4m^2+20mn+25n^2)
U brojiniku imas mn (stupnja 2)
U nazivniku m^2, n^2 i mn, takodjer sve stupnja 2.
Kad bi bio neki izraz tipa (m^2+n^2)/(m^2+n), ne bi mogli ovo napraviti jer bi se u nazivniku pojavio n/m^2. Kako zelimo supstituirati q=n/m, ovo nam ne bi pasalo.
Btw, nisam ipak tolko stariji :P[/quote]
Malo sam dosadna, razumijem sve, al kako je mn stupnja 2 ? mm, nn ok, al mn ? :roll:
P.s. :D
| pbakic (napisa): | Homogeno ovdje znaci da je svaki dio izraza istog stupnja:
razlomak je: 10mn/(4m^2+20mn+25n^2)
U brojiniku imas mn (stupnja 2)
U nazivniku m^2, n^2 i mn, takodjer sve stupnja 2.
Kad bi bio neki izraz tipa (m^2+n^2)/(m^2+n), ne bi mogli ovo napraviti jer bi se u nazivniku pojavio n/m^2. Kako zelimo supstituirati q=n/m, ovo nam ne bi pasalo.
Btw, nisam ipak tolko stariji |
Malo sam dosadna, razumijem sve, al kako je mn stupnja 2 ? mm, nn ok, al mn ? 
P.s. 
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)
Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol:
|
| Postano: 17:53 čet, 6. 1. 2011 Naslov: |
|
|
|
Ma nista posebno, kad imas polinom dvije (ili vise) varijable, onda zbrajas sve stupnjeve u nekom monomu, npr:
x^2y^3 ... stupanj x je 2, stupanj y je 3, ukupno je stupanj 5
Ma nista posebno, kad imas polinom dvije (ili vise) varijable, onda zbrajas sve stupnjeve u nekom monomu, npr:
x^2y^3 ... stupanj x je 2, stupanj y je 3, ukupno je stupanj 5
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)
Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
| Postano: 17:59 čet, 6. 1. 2011 Naslov: |
|
|
|
[quote="pbakic"]Ma nista posebno, kad imas polinom dvije (ili vise) varijable, onda zbrajas sve stupnjeve u nekom monomu, npr:
x^2y^3 ... stupanj x je 2, stupanj y je 3, ukupno je stupanj 5[/quote]
A da,da super, hvala puno! :D
| pbakic (napisa): | Ma nista posebno, kad imas polinom dvije (ili vise) varijable, onda zbrajas sve stupnjeve u nekom monomu, npr:
x^2y^3 ... stupanj x je 2, stupanj y je 3, ukupno je stupanj 5 |
A da,da super, hvala puno!
|
|
| [Vrh] |
|
Lanek_
Forumaš(ica)
Pridružen/a: 22. 10. 2010. (18:51:42)
Postovi: (31)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)
Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol:
|
| Postano: 15:52 ned, 9. 1. 2011 Naslov: |
|
|
|
Mozes zaobici, ako mozes naslutiti infimum i supremum, pa pokazati da je izraz >= inf i <=sup, te ga postici, za neke vrijednosti m,n,p,q - koje god i koliko god varijabli bilo.
Ili eventualno doci do sup i inf koristenjem nekih nejednakosti, tipa CS, nejednakosti sredina, itd..
No ipak bih rekao da je najlakse i najsigurnije (sto se tice ovih zadataka iz kolokvija), promatrati niz, jer su uostalom zadaci napravljeni da se upravo to i ucini :)
Mozes zaobici, ako mozes naslutiti infimum i supremum, pa pokazati da je izraz >= inf i <=sup, te ga postici, za neke vrijednosti m,n,p,q - koje god i koliko god varijabli bilo.
Ili eventualno doci do sup i inf koristenjem nekih nejednakosti, tipa CS, nejednakosti sredina, itd..
No ipak bih rekao da je najlakse i najsigurnije (sto se tice ovih zadataka iz kolokvija), promatrati niz, jer su uostalom zadaci napravljeni da se upravo to i ucini 
|
|
| [Vrh] |
|
Lanek_
Forumaš(ica)
Pridružen/a: 22. 10. 2010. (18:51:42)
Postovi: (31)16
|
|
| [Vrh] |
|
Flame
Forumaš(ica)
Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol:
|
|
| [Vrh] |
|
|
