| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
Vip
Forumaš(ica)

Pridružen/a: 12. 10. 2007. (17:53:31)
Postovi: (8E)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 14:38 sri, 5. 1. 2011 Naslov: Postano: 14:38 sri, 5. 1. 2011 Naslov: |
    |
|
|
b) Treba zapravo dokazati da je skup svih pozitivno definitnih matrica otvoren. Kako? Malo se pozabavi time. :) Pogledaj dokaz prve tvrdnje u lemi [url=http://web.math.hr/nastava/difraf/dif/p_o18.pdf]ovdje[/url]. Možda ti da ideju...
c) Kao i u skripti, treba nam Taylorov teorem. On kaže da je [latex]f(x) = f(c) + \frac{1}{2} D^2 f(\bar{c})(x - c, x - c) = f(c) + \frac{1}{2} (H_f(\bar{c})(x - c) | x - c)[/latex]. E sad, bilo bi super da je [latex]H_f(\bar{c})[/latex] pozitivno definitna matrica. To bi nam dalo [latex]f(x) > f(c) + 0[/latex], za [latex]x \neq c[/latex].
Iskoristimo b). On kaže da postoji [latex]r > 0[/latex] td. [latex]K(H_f(c), r)[/latex] podskup poz. def. matrica. Funkcija [latex]f[/latex] je klase [latex]C^2[/latex], pa je [latex]D^2 f \leftrightarrow H_f[/latex] neprekidna. Slijedi da postoji [latex]\delta > 0[/latex] td. [latex]\| x - c \| < \delta[/latex] povlači [latex]\| H_f(x) - H_f(c) \| < r[/latex].
To je otprilike to. Uzmemo proizvoljan [latex]x \in \mathbb{R}^n[/latex] td. [latex]\| x - c \| < \delta[/latex] i vratimo se Tayloru. On kaže da je [latex]\bar{c} \in \langle c, x \rangle[/latex], pa je [latex]\| \bar{c} - c \| < \delta[/latex]. Slijedi [latex]\| H_f(\bar{c}) - H_f(c) \| < r[/latex]. Dakle, [latex]H_f(\bar{c})[/latex] je pozitivno definitna.
b) Treba zapravo dokazati da je skup svih pozitivno definitnih matrica otvoren. Kako? Malo se pozabavi time.  Pogledaj dokaz prve tvrdnje u lemi ovdje. Možda ti da ideju... Pogledaj dokaz prve tvrdnje u lemi ovdje. Možda ti da ideju...
c) Kao i u skripti, treba nam Taylorov teorem. On kaže da je 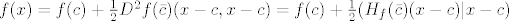 . E sad, bilo bi super da je . E sad, bilo bi super da je 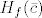 pozitivno definitna matrica. To bi nam dalo pozitivno definitna matrica. To bi nam dalo 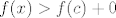 , za , za 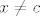 . .
Iskoristimo b). On kaže da postoji 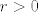 td. td. 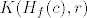 podskup poz. def. matrica. Funkcija podskup poz. def. matrica. Funkcija  je klase je klase 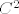 , pa je , pa je 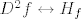 neprekidna. Slijedi da postoji neprekidna. Slijedi da postoji 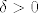 td. td. 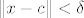 povlači povlači 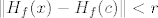 . .
To je otprilike to. Uzmemo proizvoljan  td. td. 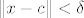 i vratimo se Tayloru. On kaže da je i vratimo se Tayloru. On kaže da je 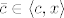 , pa je , pa je 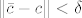 . Slijedi . Slijedi 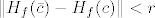 . Dakle, . Dakle, 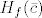 je pozitivno definitna. je pozitivno definitna.
|
|
| [Vrh] |
|
Vip
Forumaš(ica)

Pridružen/a: 12. 10. 2007. (17:53:31)
Postovi: (8E)16
Spol: 
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 10:13 čet, 6. 1. 2011 Naslov: Postano: 10:13 čet, 6. 1. 2011 Naslov: |
    |
|
|
Ovako glasi zadatak: Nađite ekstreme funkcije [latex] f(x,y,z)=x^2+2y^2-z^2[/latex] na [latex]D=\{(x,y) \in \mathbb{R}^2 ; x^2+y^2 \leq 1, x+z=2\}[/latex]
znam da se maximum postiže na D(jer je kompaktan i f je neprekidna), i da bih trebala gledati IntD, i rub od D posebno,ali baš mi nije jasno kako da to napravim..
Ovako glasi zadatak: Nađite ekstreme funkcije 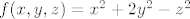 na na 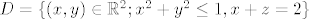
znam da se maximum postiže na D(jer je kompaktan i f je neprekidna), i da bih trebala gledati IntD, i rub od D posebno,ali baš mi nije jasno kako da to napravim..
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 13:47 čet, 6. 1. 2011 Naslov: Postano: 13:47 čet, 6. 1. 2011 Naslov: |
    |
|
|
Pa tu bi proslo valjda obicno uvrstavanje z=2-x
Onda dobijemo funkciju dvije varijable (x i y) za koju trazimo ekstreme u jedinicnoj kugli:
prvo provjerimo interior - trazimo stacionarne tocke, gledamo Hesseovu matricu, itd.
nakon toga, provjeravamo rub:
tu trazimo ekstreme funkcije f(x,y) na skupu x^2+y^2=1, a to znamo pomocu Lagrangeovog multiplikatora
Pa tu bi proslo valjda obicno uvrstavanje z=2-x
Onda dobijemo funkciju dvije varijable (x i y) za koju trazimo ekstreme u jedinicnoj kugli:
prvo provjerimo interior - trazimo stacionarne tocke, gledamo Hesseovu matricu, itd.
nakon toga, provjeravamo rub:
tu trazimo ekstreme funkcije f(x,y) na skupu x^2+y^2=1, a to znamo pomocu Lagrangeovog multiplikatora
|
|
| [Vrh] |
|
šišmiš
Forumaš(ica)

Pridružen/a: 19. 04. 2010. (21:01:19)
Postovi: (29)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 23:48 čet, 6. 1. 2011 Naslov: Postano: 23:48 čet, 6. 1. 2011 Naslov: |
    |
|
|
[quote="šišmiš"]nije mi jasna ova ocjena pogreske :S kako nju oderediti[/quote]
To je malo čudno pitanje. Valjda se samo očekuje da se napiše da postoji c između 0 i x te d između 0 i y td. je ostatak [latex]\frac{1}{4!} D^4f(c, d)((x, y), (x, y), (x, y), (x, y)) = \frac{1}{4!} \sin c \, x^4[/latex].
1.b) Nije cijeli [latex]\mathbb{R}^2[/latex]. U [latex](\mathbb{R} \setminus \{0\} \times \{0\}) \cup (\{0\} \times \mathbb{R} \setminus \{0\})[/latex] je "oštro".
5. Pogledaj iskaz teorema o inverznom preslikavanju. On će reći na kojem dijelu je moguće invertirati. Za ostatak se može pokazati da nejde (promotri sliku).
6. Najlakše preko parcijalnih. Za ostatak kaže da ga treba "opisati". To bi trebalo značiti da je dovoljno napisati: "Postoji [latex]c \in \langle 0, x \rangle[/latex] td. je ostatak [latex]\frac{1}{3!} D^3(c)(x, x, x)[/latex]."
| šišmiš (napisa): | | nije mi jasna ova ocjena pogreske :S kako nju oderediti |
To je malo čudno pitanje. Valjda se samo očekuje da se napiše da postoji c između 0 i x te d između 0 i y td. je ostatak 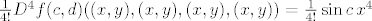 . .
1.b) Nije cijeli 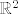 . U . U 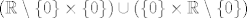 je "oštro". je "oštro".
5. Pogledaj iskaz teorema o inverznom preslikavanju. On će reći na kojem dijelu je moguće invertirati. Za ostatak se može pokazati da nejde (promotri sliku).
6. Najlakše preko parcijalnih. Za ostatak kaže da ga treba "opisati". To bi trebalo značiti da je dovoljno napisati: "Postoji 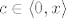 td. je ostatak td. je ostatak 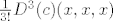 ." ."
|
|
| [Vrh] |
|
šišmiš
Forumaš(ica)

Pridružen/a: 19. 04. 2010. (21:01:19)
Postovi: (29)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
Black Mamba
Forumaš(ica)

Pridružen/a: 12. 10. 2009. (21:08:31)
Postovi: (58)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
Vip
Forumaš(ica)

Pridružen/a: 12. 10. 2007. (17:53:31)
Postovi: (8E)16
Spol: 
|
|
| [Vrh] |
|
šišmiš
Forumaš(ica)

Pridružen/a: 19. 04. 2010. (21:01:19)
Postovi: (29)16
|
 Postano: 16:56 pet, 7. 1. 2011 Naslov: Postano: 16:56 pet, 7. 1. 2011 Naslov: |
    |
|
|
http://web.math.hr/nastava/difraf/dif/2007-08/tangencijalna.pdf
kako bi 4 zadatak ?????
http://web.math.hr/nastava/difraf/dif/2008-09/kolokvij2.pdf
2 zadatak- kako bi to ?
3a) jesam li sa skroz zbunjen ili kaj?- dobijem da je y^2=-1 ?
3b) ne razumijem bas pitanje, funkcija ima minimum u (0,2/9), kako se sad mene pita jel ima min i maks na elipsi? opcenito nema...
ili se mene trazi da ja nadem najmanju i najvecu vrijednost jer je elipsa kompaktna??
ne razuumijem baš ?!?!?! :SS
i kako se inace gleda jel funk ima GLOBALNE ekstreme? ako nema uvjeta nikakvih- samo izracunam stacionarne, provjerim i to je to?
[size=9][color=#999999]Added after 53 minutes:[/color][/size]
http://web.math.hr/nastava/difraf/dif/2007-08/tangencijalna.pdf
prvi zadatak rjesavam...
nadem derivacije po x i y, dobijem normalu u tocki- (-48/5, -12/5, -208/5) ?valjda...
i sada kako napisat jednandzu tang ravnine kada mi fali z?
fakat ne razumijem :S
sta ne bi tocka M koja je zadana trebala izgledati M(x,y,z)???
http://web.math.hr/nastava/difraf/dif/2007-08/tangencijalna.pdf
kako bi 4 zadatak ?????
http://web.math.hr/nastava/difraf/dif/2008-09/kolokvij2.pdf
2 zadatak- kako bi to ?
3a) jesam li sa skroz zbunjen ili kaj?- dobijem da je y^2=-1 ?
3b) ne razumijem bas pitanje, funkcija ima minimum u (0,2/9), kako se sad mene pita jel ima min i maks na elipsi? opcenito nema...
ili se mene trazi da ja nadem najmanju i najvecu vrijednost jer je elipsa kompaktna??
ne razuumijem baš ?!?!?! :SS
i kako se inace gleda jel funk ima GLOBALNE ekstreme? ako nema uvjeta nikakvih- samo izracunam stacionarne, provjerim i to je to?
Added after 53 minutes:
http://web.math.hr/nastava/difraf/dif/2007-08/tangencijalna.pdf
prvi zadatak rjesavam...
nadem derivacije po x i y, dobijem normalu u tocki- (-48/5, -12/5, -208/5) ?valjda...
i sada kako napisat jednandzu tang ravnine kada mi fali z?
fakat ne razumijem :S
sta ne bi tocka M koja je zadana trebala izgledati M(x,y,z)???
|
|
| [Vrh] |
|
Black Mamba
Forumaš(ica)

Pridružen/a: 12. 10. 2009. (21:08:31)
Postovi: (58)16
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
Black Mamba
Forumaš(ica)

Pridružen/a: 12. 10. 2009. (21:08:31)
Postovi: (58)16
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 20:11 pet, 7. 1. 2011 Naslov: Postano: 20:11 pet, 7. 1. 2011 Naslov: |
    |
|
|
[quote=".anchy."]Ovako glasi zadatak: Nađite ekstreme funkcije [latex] f(x,y,z)=x^2+2y^2-z^2[/latex] na [latex]D=\{(x,y) \in \mathbb{R}^2 ; x^2+y^2 \leq 1, x+z=2\}[/latex]
znam da se maximum postiže na D(jer je kompaktan i f je neprekidna), i da bih trebala gledati IntD, i rub od D posebno,ali baš mi nije jasno kako da to napravim..[/quote]
glupo kaj citiram samu sebe,ali može netko napisati rješenja?
Meni je ispalo da je max u (1,0,1) a min u (-1,0,3)
| .anchy. (napisa): | Ovako glasi zadatak: Nađite ekstreme funkcije 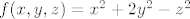 na na 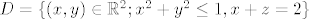
znam da se maximum postiže na D(jer je kompaktan i f je neprekidna), i da bih trebala gledati IntD, i rub od D posebno,ali baš mi nije jasno kako da to napravim.. |
glupo kaj citiram samu sebe,ali može netko napisati rješenja?
Meni je ispalo da je max u (1,0,1) a min u (-1,0,3)
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 23:00 pet, 7. 1. 2011 Naslov: Postano: 23:00 pet, 7. 1. 2011 Naslov: |
    |
|
|
Meni isto :D
Btw, mislim da je 1.11 iz ovih vjezbi max. funkcije xyz (jer to je volumen kvadra ciji je jedan vrh u 0,0,0 a drugi u x,y,z) uz uvjet x^2+y^2+z-1=0
Meni isto 
Btw, mislim da je 1.11 iz ovih vjezbi max. funkcije xyz (jer to je volumen kvadra ciji je jedan vrh u 0,0,0 a drugi u x,y,z) uz uvjet x^2+y^2+z-1=0
|
|
| [Vrh] |
|
homesweethome
Forumaš(ica)

Pridružen/a: 21. 10. 2009. (16:25:25)
Postovi: (1C)16
|
 Postano: 1:26 sub, 8. 1. 2011 Naslov: Postano: 1:26 sub, 8. 1. 2011 Naslov: |
    |
|
|
http://web.math.hr/nastava/difraf/dif/2009-10/kolokvij2.pdf
zanima me zadatak 3.(b)
Postavila sam fju kao [code:1]f(x,y,z)=x*y*z, uz uvjet da je x*y+x*z+y*z=27, te x,y,z>0[/code:1] , ali dalje ne ide.. :)
http://web.math.hr/nastava/difraf/dif/2009-10/kolokvij2.pdf
zanima me zadatak 3.(b)
Postavila sam fju kao | Kod: | | f(x,y,z)=x*y*z, uz uvjet da je x*y+x*z+y*z=27, te x,y,z>0 |
, ali dalje ne ide.. 
|
|
| [Vrh] |
|
|














