|
Mogao si i napisati kuda ide [latex]x[/latex], ali 'ajde, ljudi smo. :) (Pretpostavljam, u nulu.)
Uglavnom, ovak. :) Ta tvoja prokletinja nema limes. :P Stvar divergira u [latex]+\infty[/latex] zdesna, a u [latex]-\infty[/latex] slijeva. To čak i nije tako teško pokazati: prvo množimo i brojnik i nazivnik s [latex]\sqrt{\cos(14x)}e^{34x}-1[/latex]. Sad gore imamo razliku kvadrata i dobivamo da tražimo limes od [latex]\displaystyle\frac{\cos(14x)e^{68x}-1}{\tan^2(4x)(\sqrt{\cos(14x)}e^{34x}+1)}[/latex].
E, sad, s ovom zagradom dolje nemamo problema, a gore ćemo probati dovesti to na tablične limese za kosinus i eksponencijalnu funkciju. Zato ćemo brojnik malo rearanžirati: [latex]\cos(14x)e^{68x}-1=(\cos(14x)-1)(e^{68x}-1)+(e^{68x}-1)+(\cos(x)-1)[/latex]. No dobro, sad već polako počinjemo osjećati o čemu se radi. Naime, znamo da je [latex]e^{68x}-1[/latex] "usporediv" s [latex]x[/latex], [latex]\cos(x)-1[/latex] s [latex]x^2[/latex], a onda je ovaj umnožak zagrada na početku "usporediv" s [latex]x^3[/latex]. Budući da je nazivnik "usporediv" s [latex]x^2[/latex], idemo i brojnik i nazivnik podijeliti s time.
Dobivamo, kad iskoristimo sve ovo gore, [latex]\displaystyle\frac{\frac{\cos(14x)-1}{(14x)^2}\cdot\frac{e^{68x}-1}{68x}\cdot 14^2\cdot 68\cdot x+\frac{e^{68x}-1}{68x}\cdot\frac{68}{x}+\frac{\cos(14x)-1}{(14x)^2}\cdot 14^2}{\frac{\tan^2(4x)}{(4x)^2}\cdot 4^2\cdot (\sqrt{\cos(14x)}e^{34x}+1)}[/latex].
E, i sad smo, vjerovao ili ne, riješili zadatak. :) Naime, znamo limes od [latex]\displaystyle\frac{\tan(x)}{x}[/latex] u nuli, pa nazivnik očito ide u nešto pozitivno (specifično, [latex]1\cdot 4^2\cdot 2=32[/latex], ako se ne varam, ali nebitno je). U brojniku prvi pribrojnik ide u [latex]0[/latex] (prvi razlomak ima konačni limes, kao i drugi, a [latex]x\to 0[/latex]), dok treći ide u nešto pozitivno ([latex]\displaystyle -\frac{14^2}{2}=-98[/latex] ili tako nešto). No, drugi pribrojnik "naliči na [latex]\frac{1}{x}[/latex]": naime, ovaj prvi razlomak ide u [latex]1[/latex], dok drugi ide u [latex]+\infty[/latex] za [latex]x\to 0+[/latex], a u [latex]-\infty[/latex] za [latex]x\to 0-[/latex].
Stoga, za [latex]x\to 0+[/latex], ovo sve zajedno ide u [latex]\displaystyle\frac{0+\infty-98}{32}=+\infty[/latex] (naravno, ovo je čisto zlorabljenje notacije, nije nimalo precizno, ali jasno je na što ciljam), a za [latex]x\to 0-[/latex], ide u [latex]\displaystyle\frac{0-\infty-98}{32}=-\infty[/latex], čime smo dokazali tvrdnju koju sam izrekao još onomad, kad sam počeo pisati ovaj post. :)
Mogao si i napisati kuda ide  , ali 'ajde, ljudi smo. , ali 'ajde, ljudi smo.  (Pretpostavljam, u nulu.) (Pretpostavljam, u nulu.)
Uglavnom, ovak.  Ta tvoja prokletinja nema limes. Ta tvoja prokletinja nema limes.  Stvar divergira u Stvar divergira u  zdesna, a u zdesna, a u 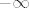 slijeva. To čak i nije tako teško pokazati: prvo množimo i brojnik i nazivnik s slijeva. To čak i nije tako teško pokazati: prvo množimo i brojnik i nazivnik s 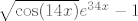 . Sad gore imamo razliku kvadrata i dobivamo da tražimo limes od . Sad gore imamo razliku kvadrata i dobivamo da tražimo limes od 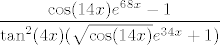 . .
E, sad, s ovom zagradom dolje nemamo problema, a gore ćemo probati dovesti to na tablične limese za kosinus i eksponencijalnu funkciju. Zato ćemo brojnik malo rearanžirati: 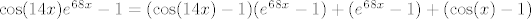 . No dobro, sad već polako počinjemo osjećati o čemu se radi. Naime, znamo da je . No dobro, sad već polako počinjemo osjećati o čemu se radi. Naime, znamo da je 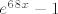 "usporediv" s "usporediv" s  , , 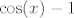 s s 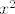 , a onda je ovaj umnožak zagrada na početku "usporediv" s , a onda je ovaj umnožak zagrada na početku "usporediv" s 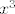 . Budući da je nazivnik "usporediv" s . Budući da je nazivnik "usporediv" s 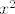 , idemo i brojnik i nazivnik podijeliti s time. , idemo i brojnik i nazivnik podijeliti s time.
Dobivamo, kad iskoristimo sve ovo gore, 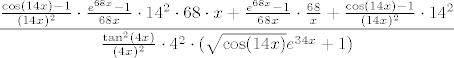 . .
E, i sad smo, vjerovao ili ne, riješili zadatak.  Naime, znamo limes od Naime, znamo limes od 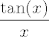 u nuli, pa nazivnik očito ide u nešto pozitivno (specifično, u nuli, pa nazivnik očito ide u nešto pozitivno (specifično, 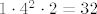 , ako se ne varam, ali nebitno je). U brojniku prvi pribrojnik ide u , ako se ne varam, ali nebitno je). U brojniku prvi pribrojnik ide u  (prvi razlomak ima konačni limes, kao i drugi, a (prvi razlomak ima konačni limes, kao i drugi, a 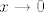 ), dok treći ide u nešto pozitivno ( ), dok treći ide u nešto pozitivno (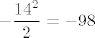 ili tako nešto). No, drugi pribrojnik "naliči na ili tako nešto). No, drugi pribrojnik "naliči na  ": naime, ovaj prvi razlomak ide u ": naime, ovaj prvi razlomak ide u  , dok drugi ide u , dok drugi ide u  za za 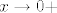 , a u , a u 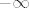 za za 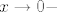 . .
Stoga, za 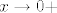 , ovo sve zajedno ide u , ovo sve zajedno ide u 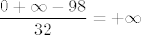 (naravno, ovo je čisto zlorabljenje notacije, nije nimalo precizno, ali jasno je na što ciljam), a za (naravno, ovo je čisto zlorabljenje notacije, nije nimalo precizno, ali jasno je na što ciljam), a za 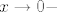 , ide u , ide u 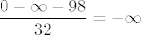 , čime smo dokazali tvrdnju koju sam izrekao još onomad, kad sam počeo pisati ovaj post. , čime smo dokazali tvrdnju koju sam izrekao još onomad, kad sam počeo pisati ovaj post. 
|





