| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 9:52 sub, 8. 1. 2011 Naslov: Postano: 9:52 sub, 8. 1. 2011 Naslov: |
    |
|
|
[quote="homesweethome"]http://web.math.hr/nastava/difraf/dif/2009-10/kolokvij2.pdf
zanima me zadatak 3.(b)
Postavila sam fju kao [code:1]f(x,y,z)=x*y*z, uz uvjet da je x*y+x*z+y*z=27, te x,y,z>0[/code:1] , ali dalje ne ide.. :)[/quote]
taj zad i mene muči, radila sam pomoću Lagr.multipl., dobila jednadžbe[latex]bc=\lambda(b+c) ,
ac=\lambda(a+c) ,
ba=\lambda(b+a)
[/latex]
i onda sam izrazila c pomoću b iz prve jedn.,uvrstila u treću i izrazila a pomoću c,i dobila
[latex]\frac{c^2}{\lambda}-c-\lambda*c=0
[/latex]
i sada neznam što dalje..
| homesweethome (napisa): | http://web.math.hr/nastava/difraf/dif/2009-10/kolokvij2.pdf
zanima me zadatak 3.(b)
Postavila sam fju kao | Kod: | | f(x,y,z)=x*y*z, uz uvjet da je x*y+x*z+y*z=27, te x,y,z>0 |
, ali dalje ne ide..  |
taj zad i mene muči, radila sam pomoću Lagr.multipl., dobila jednadžbe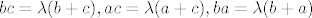
i onda sam izrazila c pomoću b iz prve jedn.,uvrstila u treću i izrazila a pomoću c,i dobila
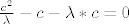
i sada neznam što dalje..
|
|
| [Vrh] |
|
ante c
Forumaš(ica)


Pridružen/a: 10. 10. 2009. (19:18:15)
Postovi: (62)16
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 16:06 sub, 8. 1. 2011 Naslov: Postano: 16:06 sub, 8. 1. 2011 Naslov: |
    |
|
|
http://web.math.hr/nastava/ma34/ma3/2006-07/20070207_3.pdf
može li netko riješiti 3.zad? to mi nije baš najjasnije,ali bez raspisivanja,preko kompozicije. Ovako sam počela:
f1(x,y)=<a,x>
f2(x,y)=y
f3(x,y)=b*cosx
f4(x,y)=||x||^2
i sada sam zapela kod određivanja diferencijala..
Sumnjam da sam točno riješila:
Df1(x,y)(H1,H2??)=<a,H1>
Df2(x,y)(H1,H2)=H2
Df3(x,y)(H1,H2)=b*sinx*H1
Df4(x,y)(H1,H2)=2<x,H1>
također,da li se 4.zad računa pomoću Hesseove matrice ili ipak postoji lakši način?ružni su mi ovi korijeni :P
http://web.math.hr/nastava/ma34/ma3/2006-07/20070207_3.pdf
može li netko riješiti 3.zad? to mi nije baš najjasnije,ali bez raspisivanja,preko kompozicije. Ovako sam počela:
f1(x,y)=<a,x>
f2(x,y)=y
f3(x,y)=b*cosx
f4(x,y)=||x||^2
i sada sam zapela kod određivanja diferencijala..
Sumnjam da sam točno riješila:
Df1(x,y)(H1,H2??)=<a,H1>
Df2(x,y)(H1,H2)=H2
Df3(x,y)(H1,H2)=b*sinx*H1
Df4(x,y)(H1,H2)=2<x,H1>
također,da li se 4.zad računa pomoću Hesseove matrice ili ipak postoji lakši način?ružni su mi ovi korijeni 
|
|
| [Vrh] |
|
ante c
Forumaš(ica)


Pridružen/a: 10. 10. 2009. (19:18:15)
Postovi: (62)16
|
|
| [Vrh] |
|
homesweethome
Forumaš(ica)

Pridružen/a: 21. 10. 2009. (16:25:25)
Postovi: (1C)16
|
 Postano: 18:00 sub, 8. 1. 2011 Naslov: Postano: 18:00 sub, 8. 1. 2011 Naslov: |
    |
|
|
[quote="ante c"][latex]
bc=\lambda(b+c) ,
ac=\lambda(a+c) ,
ba=\lambda(b+a)
[/latex]
iz ovoga upravo imaš da ti je a=b=c(x=y=z) i nakon toga to vratiš u jednadžbu uvjeta
(onu da je oplošje 54)[/quote]
Ok, i dobijem da je stacionarna tocka (3,3,3), kako sada prokomentirati to da je to tocka globalnog maksimuma na S, ak uopce jest..
| ante c (napisa): | 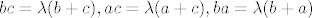
iz ovoga upravo imaš da ti je a=b=c(x=y=z) i nakon toga to vratiš u jednadžbu uvjeta
(onu da je oplošje 54) |
Ok, i dobijem da je stacionarna tocka (3,3,3), kako sada prokomentirati to da je to tocka globalnog maksimuma na S, ak uopce jest..
|
|
| [Vrh] |
|
ante c
Forumaš(ica)


Pridružen/a: 10. 10. 2009. (19:18:15)
Postovi: (62)16
|
 Postano: 18:20 sub, 8. 1. 2011 Naslov: Postano: 18:20 sub, 8. 1. 2011 Naslov: |
    |
|
|
sada imaš funkciju u 4 varijable(x,y,z,lambda)
lambda ti je 9/6 ak se ne varam i onda hessova matrica i prvojeriš trebale bi ti sve svojstvene vrijednosti bit veće od nula ......iako čak mislim ali nisam siguran da je dovoljno gledati samo drugu derivaciju od funkcije f(x,y,z)=x*y*z i njenu pripadnu hessovu matricu u točki (3,3,3)
sada imaš funkciju u 4 varijable(x,y,z,lambda)
lambda ti je 9/6 ak se ne varam i onda hessova matrica i prvojeriš trebale bi ti sve svojstvene vrijednosti bit veće od nula ......iako čak mislim ali nisam siguran da je dovoljno gledati samo drugu derivaciju od funkcije f(x,y,z)=x*y*z i njenu pripadnu hessovu matricu u točki (3,3,3)
|
|
| [Vrh] |
|
Black Mamba
Forumaš(ica)

Pridružen/a: 12. 10. 2009. (21:08:31)
Postovi: (58)16
|
 Postano: 19:17 sub, 8. 1. 2011 Naslov: Postano: 19:17 sub, 8. 1. 2011 Naslov: |
    |
|
|
[quote="pmli"][quote="šišmiš"]taj 1b- kako bi to pokazao ?[/quote]
Pokažeš da ne postoji limes iz definicije parcijalne derivacije. Uzmeš točku [latex](x, 0)[/latex] ([latex]x \neq 0[/latex]) i promatraš [latex]\displaystyle \lim_{h \to 0} \frac{f(x, h) - f(x, 0)}{h}[/latex].
[quote="šišmiš"]a 5 zad mi nije jasan bas; jer taj iskaz pola razumjem pola ne :S[/quote]
Koja polovica? :) Uglavnom, trebaš izračunati Jacobijevu matricu i odrediti za koje je sve točke regularna.[/quote]
Kada nađem da je funkcija invertibilna za sve točke (r,0,z) gdje je r različito 0, moram li nekako posebno dokazivat da nije invertibilna kada je r=0, ili to jednostavno proizlazi iz toga da je determinanta Jacobijeve matrice tada jednaka nuli?
| pmli (napisa): | | šišmiš (napisa): | | taj 1b- kako bi to pokazao ? |
Pokažeš da ne postoji limes iz definicije parcijalne derivacije. Uzmeš točku 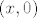 ( (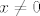 ) i promatraš ) i promatraš 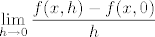 . .
| šišmiš (napisa): | | a 5 zad mi nije jasan bas; jer taj iskaz pola razumjem pola ne :S |
Koja polovica?  Uglavnom, trebaš izračunati Jacobijevu matricu i odrediti za koje je sve točke regularna. Uglavnom, trebaš izračunati Jacobijevu matricu i odrediti za koje je sve točke regularna. |
Kada nađem da je funkcija invertibilna za sve točke (r,0,z) gdje je r različito 0, moram li nekako posebno dokazivat da nije invertibilna kada je r=0, ili to jednostavno proizlazi iz toga da je determinanta Jacobijeve matrice tada jednaka nuli?
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 19:47 sub, 8. 1. 2011 Naslov: Postano: 19:47 sub, 8. 1. 2011 Naslov: |
    |
|
|
Što više učim,to manje znam :(
Počela sam rješavat neke zadatke,i neznam ih riješit do kraja..
http://web.math.hr/nastava/difraf/dif/2006-07/zadaca3.pdf
zad 10.(ii) ovo s parc.derivacijama
dobim da je npr.parcijalna derivacija po x 2xsin(1/x)-cos(1/x), i sada neznam izračunati limes kada (x,y)->(0,y)
i kod takvog zadatka,trebam li gledati posebno parc.der. u (x,y)!=(0,0) i (x,y)=(0,0) ili mogu gledati samo jedan slučaj?
http://web.math.hr/nastava/difraf/dif/2009-10/kolokvij2.pdf
1.(b)
dobila sam da mi je kandidat za zapis diferencijala (2 3), to sam uvrstila u def.diferencijabilnosti f-je i meni ispada lim(-xy(2y+3x))=0, a mislim da mi to nesmije ispast :?:
http://web.math.hr/nastava/difraf/dif/2008-09/kolokvij2.pdf
3.(b)
Stacionarne točke mi ispadnu (0,5/2), (0,-5/2),(3,1)(-3,1)
a Hesseova matrica mi ispada
(2 0)
(0 9)
za svaki (x,y) što bi značilo da su to sve minimumi jer je matrica poz.definitna, a uvrštavanjem se vidi da u tim točkama f-.ja ne poprima iste vrijednosti :?:
http://web.math.hr/nastava/difraf/dif/2006-07/zadaca3.pdf
zad12.
Dobijem za (x,y)!=(0,0)
df/dx=y^3/(x^2+y^2)^(3/2)
a u (0,0)=0
i sada kada provjeravam pomoću neprekidnosti parc.derivacija, trebam li gledati lim(y^3/(x^2+y^2)^(3/2)) kada (x,y)->(0,0) i on mi mora biti jednak 0?
ako da,može netko izračunat taj limes? zaboravila sam kako to ide.. :oops:
Odredite ekstreme funkcije f(x,y,z)=xz-y^2 na skupu S={(x,y,z):x^2+y^2+z^2=9}
dobila sam
z=2*lambda*x
x=2*lambda*z
-2y=2*lambda*y
iz prva 2 uvjeta slijedi da je x^2=z^2, a iz zadnjeg lambda=-1 ili y=0
sad me muči,ako je lambda = -1,ništa ne dobivam iz toga?
pa sam ostavila samo y=0,pa je x=+-3/sqrt2, z=+-3/sqrt2,je to dobro?
Što više učim,to manje znam 
Počela sam rješavat neke zadatke,i neznam ih riješit do kraja..
http://web.math.hr/nastava/difraf/dif/2006-07/zadaca3.pdf
zad 10.(ii) ovo s parc.derivacijama
dobim da je npr.parcijalna derivacija po x 2xsin(1/x)-cos(1/x), i sada neznam izračunati limes kada (x,y)->(0,y)
i kod takvog zadatka,trebam li gledati posebno parc.der. u (x,y)!=(0,0) i (x,y)=(0,0) ili mogu gledati samo jedan slučaj?
http://web.math.hr/nastava/difraf/dif/2009-10/kolokvij2.pdf
1.(b)
dobila sam da mi je kandidat za zapis diferencijala (2 3), to sam uvrstila u def.diferencijabilnosti f-je i meni ispada lim(-xy(2y+3x))=0, a mislim da mi to nesmije ispast 
http://web.math.hr/nastava/difraf/dif/2008-09/kolokvij2.pdf
3.(b)
Stacionarne točke mi ispadnu (0,5/2), (0,-5/2),(3,1)(-3,1)
a Hesseova matrica mi ispada
(2 0)
(0 9)
za svaki (x,y) što bi značilo da su to sve minimumi jer je matrica poz.definitna, a uvrštavanjem se vidi da u tim točkama f-.ja ne poprima iste vrijednosti 
http://web.math.hr/nastava/difraf/dif/2006-07/zadaca3.pdf
zad12.
Dobijem za (x,y)!=(0,0)
df/dx=y^3/(x^2+y^2)^(3/2)
a u (0,0)=0
i sada kada provjeravam pomoću neprekidnosti parc.derivacija, trebam li gledati lim(y^3/(x^2+y^2)^(3/2)) kada (x,y)->(0,0) i on mi mora biti jednak 0?
ako da,može netko izračunat taj limes? zaboravila sam kako to ide.. 
Odredite ekstreme funkcije f(x,y,z)=xz-y^2 na skupu S={(x,y,z) ^2+y^2+z^2=9} ^2+y^2+z^2=9}
dobila sam
z=2*lambda*x
x=2*lambda*z
-2y=2*lambda*y
iz prva 2 uvjeta slijedi da je x^2=z^2, a iz zadnjeg lambda=-1 ili y=0
sad me muči,ako je lambda = -1,ništa ne dobivam iz toga?
pa sam ostavila samo y=0,pa je x=+-3/sqrt2, z=+-3/sqrt2,je to dobro?
|
|
| [Vrh] |
|
Black Mamba
Forumaš(ica)

Pridružen/a: 12. 10. 2009. (21:08:31)
Postovi: (58)16
|
 Postano: 19:56 sub, 8. 1. 2011 Naslov: Postano: 19:56 sub, 8. 1. 2011 Naslov: |
    |
|
|
[quote=".anchy."]Što više učim,to manje znam :(
Počela sam rješavat neke zadatke,i neznam ih riješit do kraja..
http://web.math.hr/nastava/difraf/dif/2008-09/kolokvij2.pdf
3.(b)
Stacionarne točke mi ispadnu (0,5/2), (0,-5/2),(3,1)(-3,1)
a Hesseova matrica mi ispada
(2 0)
(0 9)
za svaki (x,y) što bi značilo da su to sve minimumi jer je matrica poz.definitna, a uvrštavanjem se vidi da u tim točkama f-.ja ne poprima iste vrijednosti :?: [/quote]
Nije ti potrebna Hesseova matrica...gledaš ekstreme unutar elipse koja je kompaktan skup, a funkcija ti je neprekidna, što znači da na elipsi postiže minimum i maksimum...dakle dovoljno je odrediti vrijednosti funkcije u tim točkama, i vidjeti koja je najveća (maksimum) i najmanja( minimum)....s tim da meni točke ispadaju (0,5/2),(0,-5/2) i (-3 ,2), (3,2).... :?:
| .anchy. (napisa): | Što više učim,to manje znam 
Počela sam rješavat neke zadatke,i neznam ih riješit do kraja..
http://web.math.hr/nastava/difraf/dif/2008-09/kolokvij2.pdf
3.(b)
Stacionarne točke mi ispadnu (0,5/2), (0,-5/2),(3,1)(-3,1)
a Hesseova matrica mi ispada
(2 0)
(0 9)
za svaki (x,y) što bi značilo da su to sve minimumi jer je matrica poz.definitna, a uvrštavanjem se vidi da u tim točkama f-.ja ne poprima iste vrijednosti  |
Nije ti potrebna Hesseova matrica...gledaš ekstreme unutar elipse koja je kompaktan skup, a funkcija ti je neprekidna, što znači da na elipsi postiže minimum i maksimum...dakle dovoljno je odrediti vrijednosti funkcije u tim točkama, i vidjeti koja je najveća (maksimum) i najmanja( minimum)....s tim da meni točke ispadaju (0,5/2),(0,-5/2) i (-3 ,2), (3,2).... 
|
|
| [Vrh] |
|
homesweethome
Forumaš(ica)

Pridružen/a: 21. 10. 2009. (16:25:25)
Postovi: (1C)16
|
 Postano: 20:09 sub, 8. 1. 2011 Naslov: Postano: 20:09 sub, 8. 1. 2011 Naslov: |
    |
|
|
I ja sam zapela na tom zadatku, tocke su mi (3,2) (-3,2) (0, 5/2) (0,-5/2)
i prve dvije su mi tocke glob min, četvrta glob max, a treća.. niš. meni ima smisla... :lol:
I ja sam zapela na tom zadatku, tocke su mi (3,2) (-3,2) (0, 5/2) (0,-5/2)
i prve dvije su mi tocke glob min, četvrta glob max, a treća.. niš. meni ima smisla... 
|
|
| [Vrh] |
|
Black Mamba
Forumaš(ica)

Pridružen/a: 12. 10. 2009. (21:08:31)
Postovi: (58)16
|
 Postano: 20:22 sub, 8. 1. 2011 Naslov: Postano: 20:22 sub, 8. 1. 2011 Naslov: |
    |
|
|
[quote="homesweethome"]I ja sam zapela na tom zadatku, tocke su mi (3,2) (-3,2) (0, 5/2) (0,-5/2)
i prve dvije su mi tocke glob min, četvrta glob max, a treća.. niš. meni ima smisla... :lol:[/quote]
Meni se čini da nisi zapela, nego si ga riješila :)
| homesweethome (napisa): | I ja sam zapela na tom zadatku, tocke su mi (3,2) (-3,2) (0, 5/2) (0,-5/2)
i prve dvije su mi tocke glob min, četvrta glob max, a treća.. niš. meni ima smisla...  |
Meni se čini da nisi zapela, nego si ga riješila 
|
|
| [Vrh] |
|
homesweethome
Forumaš(ica)

Pridružen/a: 21. 10. 2009. (16:25:25)
Postovi: (1C)16
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 10:01 ned, 9. 1. 2011 Naslov: Postano: 10:01 ned, 9. 1. 2011 Naslov: |
    |
|
|
[quote="homesweethome"]a jel? umislit cu se 8)
nego zanima http://web.math.hr/nastava/difraf/dif/2007-08/DRFVVkol_22.pdf
drugi zadatak, kako iskoristiti uvjet da su dvije tang ravnine paralelne?
ima li to kakve veze s kolinearnosti gradijenata?[/quote]
ako su paralelne, normale su im paralelne,tj.imaju isti koef.smjera,a to znači da kada izračunaš normalu druge plohe,to je ustvari normala prve plohe :?:
nek me netko ispravi ukoliko griješim!
ako su paralelne, normale su im paralelne,tj.imaju isti koef.smjera,a to znači da kada izračunaš normalu druge plohe,to je ustvari normala prve plohe 
nek me netko ispravi ukoliko griješim!
|
|
| [Vrh] |
|
kaj
Forumaš(ica)

Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
 Postano: 11:11 ned, 9. 1. 2011 Naslov: Postano: 11:11 ned, 9. 1. 2011 Naslov: |
    |
|
|
[quote="homesweethome"]a jel? umislit cu se 8)
nego zanima http://web.math.hr/nastava/difraf/dif/2007-08/DRFVVkol_22.pdf
drugi zadatak, kako iskoristiti uvjet da su dvije tang ravnine paralelne?
ima li to kakve veze s kolinearnosti gradijenata?[/quote]
Da, to znači da postoji neki realni broj lambda tako da je jedan vektor pomnožen sa lambda jednak drugom vektoru, dobiš tri jedndadžbe i onda izračunaš točku, ja sam dobio da točka postoji, P(-1,-1,2), a lambda = -1.
Kako ti je ispalo rješenje u prvom zadatku tog kolokvija, ja sam dobio da fja nije dfb u (0,0), a pod c) mi je ispalo -9/2 ?
Da, to znači da postoji neki realni broj lambda tako da je jedan vektor pomnožen sa lambda jednak drugom vektoru, dobiš tri jedndadžbe i onda izračunaš točku, ja sam dobio da točka postoji, P(-1,-1,2), a lambda = -1.
Kako ti je ispalo rješenje u prvom zadatku tog kolokvija, ja sam dobio da fja nije dfb u (0,0), a pod c) mi je ispalo -9/2 ?
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
ante c
Forumaš(ica)


Pridružen/a: 10. 10. 2009. (19:18:15)
Postovi: (62)16
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
 Postano: 12:08 ned, 9. 1. 2011 Naslov: Postano: 12:08 ned, 9. 1. 2011 Naslov: |
    |
|
|
[quote]
http://web.math.hr/nastava/difraf/dif/2009-10/kolokvij2.pdf
1.(b)
dobila sam da mi je kandidat za zapis diferencijala (2 3), to sam uvrstila u def.diferencijabilnosti f-je i meni ispada lim(-xy(2y+3x))=0, a mislim da mi to nesmije ispast Question[/quote]
Kandidat za zapis je ok, a u def. diferen. bi trebala dobiti
lim_{r->0}(|-xy(2y+3x)|)/(|(x^(2)+y^(2))^(3/2)|), što prelaskom na polarne koordinate daje da taj limes ne postoji, odnosi ovisi o proizvoljnom kutu alpha.
[quote]i sada kada provjeravam pomoću neprekidnosti parc.derivacija, trebam li gledati lim(y^3/(x^2+y^2)^(3/2)) kada (x,y)->(0,0) i on mi mora biti jednak 0?
ako da,može netko izračunat taj limes? zaboravila sam kako to ide.. Embarassed[/quote]
Taj limes neće postojati, možemo npr. gledati restrikcije (x,0)->0 i (x,x) -> 1/(2^(3/2)).
Dakle provjeravamo prema definiciji diferencijabilnosti, jedini kandidat je nul operator, a ni tada limes ne postoji, dakle f nije diferen. u (0,0).
Kandidat za zapis je ok, a u def. diferen. bi trebala dobiti
lim_{r→0}(|-xy(2y+3x)|)/(|(x^(2)+y^(2))^(3/2)|), što prelaskom na polarne koordinate daje da taj limes ne postoji, odnosi ovisi o proizvoljnom kutu alpha.
| Citat: | i sada kada provjeravam pomoću neprekidnosti parc.derivacija, trebam li gledati lim(y^3/(x^2+y^2)^(3/2)) kada (x,y)→(0,0) i on mi mora biti jednak 0?
ako da,može netko izračunat taj limes? zaboravila sam kako to ide.. Embarassed |
Taj limes neće postojati, možemo npr. gledati restrikcije (x,0)→0 i (x,x) → 1/(2^(3/2)).
Dakle provjeravamo prema definiciji diferencijabilnosti, jedini kandidat je nul operator, a ni tada limes ne postoji, dakle f nije diferen. u (0,0).
|
|
| [Vrh] |
|
homesweethome
Forumaš(ica)

Pridružen/a: 21. 10. 2009. (16:25:25)
Postovi: (1C)16
|
|
| [Vrh] |
|
Black Mamba
Forumaš(ica)

Pridružen/a: 12. 10. 2009. (21:08:31)
Postovi: (58)16
|
|
| [Vrh] |
|
|





