| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
 Postano: 22:16 sri, 5. 1. 2011 Naslov: Rekurzivan niz(objasnjenje) Postano: 22:16 sri, 5. 1. 2011 Naslov: Rekurzivan niz(objasnjenje) |
    |
|
|
Zamolio bih nekoga uslugu pa ako mi moze rijesiti ovaj zadatak, bio bih jako zahvalan...
Pokazite da je niz (an) zadan rekuzivno s a(n+2)=1/2(an+1)*an +1/3, a1=0, a2=0 konvergentan i odredite mu limes
Mozda je za nekog zadatak banalan tj. vjerojatno za vecinu no evo nadam se da na vrijeme pitam
U biti kuzim sustinu zadatka, treba dokazati da je niz konvergentan tj. da je ogranicen i monoton te zatim ako je konvergentan ima jedinstven limes...
Moze li netko to rijesiti i objasniti mi, znam da puno trazim al eto voli bih vidjeti kako se to rjesava... Znam da smo rjesili nekoliko na vjezbama al nisam bas skuzio...
HVALA!
Zamolio bih nekoga uslugu pa ako mi moze rijesiti ovaj zadatak, bio bih jako zahvalan...
Pokazite da je niz (an) zadan rekuzivno s a(n+2)=1/2(an+1)*an +1/3, a1=0, a2=0 konvergentan i odredite mu limes
Mozda je za nekog zadatak banalan tj. vjerojatno za vecinu no evo nadam se da na vrijeme pitam
U biti kuzim sustinu zadatka, treba dokazati da je niz konvergentan tj. da je ogranicen i monoton te zatim ako je konvergentan ima jedinstven limes...
Moze li netko to rijesiti i objasniti mi, znam da puno trazim al eto voli bih vidjeti kako se to rjesava... Znam da smo rjesili nekoliko na vjezbama al nisam bas skuzio...
HVALA!
|
|
| [Vrh] |
|
Dofalol
Forumaš(ica)

Pridružen/a: 24. 10. 2010. (21:25:31)
Postovi: (15)16
Spol: 
|
 Postano: 23:45 sri, 5. 1. 2011 Naslov: Postano: 23:45 sri, 5. 1. 2011 Naslov: |
    |
|
|
Dobro si rekao, dovoljno je pokazati da je niz rastući i ograničen odozgo pa iz toga dobiješ da je konvergentan.
Činjenicu da je rastući pokažeš indukcijom.
Za bazu uzmeš [latex]a_3 = \frac13 \geq a_2= 0 \geq a_1 = 0[/latex].
Korak indukcije ti ide na foru da ako je [latex]a_{k+2} \geq a_{k+1} \geq a_k[/latex], onda je [latex]a_{k+3} = \frac12a_{k+2}a_{k+1}+\frac13 \geq \frac12a_{k+1}a_k+\frac13 = a_{k+2}[/latex]. Možda je malo čudnija indukcija nego inače, ali ništa strašno...
Sad, ako je ograničen odozgo, onda treba naći tu gornju granicu.
Pomogneš si u određivanju te granice na način da riješiš jednadžbu [latex]L = \frac12L^2 + \frac13[/latex], odnosno [latex]L^2 - 2L + \frac23 = 0[/latex] (znači, u rekurziji na mjesto članove niza umetneš [latex]L[/latex]).
Rješenja su [latex]L_{1,2} = \frac{3 \pm \sqrt{3}}{3}[/latex]. Sad, s obzirom da su ti prvi članovi manji od [latex]\frac{3 - \sqrt{3}}{3}[/latex], lako pokažeš da je upravo to gornja granica.
Sad kad je dokazano da je niz konvergentan, odrediš limes zapravo na isti način na koji si određivao gornju granicu, rješavanjem one gore kvadratne jednadžbe. Rješenja joj znaš, tako da si zapravo gotov. :D
Limes ti je isti kao i gornja granica (očito ne može biti onaj veći broj). Dakle, [latex]\lim_{n} a_n = \frac{3 - \sqrt{3}}{3}[/latex]. Nadam se da je sve jasno i da nisam nešto fulao. :P
Dobro si rekao, dovoljno je pokazati da je niz rastući i ograničen odozgo pa iz toga dobiješ da je konvergentan.
Činjenicu da je rastući pokažeš indukcijom.
Za bazu uzmeš 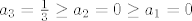 . .
Korak indukcije ti ide na foru da ako je 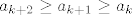 , onda je , onda je 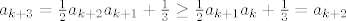 . Možda je malo čudnija indukcija nego inače, ali ništa strašno... . Možda je malo čudnija indukcija nego inače, ali ništa strašno...
Sad, ako je ograničen odozgo, onda treba naći tu gornju granicu.
Pomogneš si u određivanju te granice na način da riješiš jednadžbu 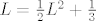 , odnosno , odnosno 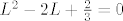 (znači, u rekurziji na mjesto članove niza umetneš (znači, u rekurziji na mjesto članove niza umetneš  ). ).
Rješenja su 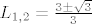 . Sad, s obzirom da su ti prvi članovi manji od . Sad, s obzirom da su ti prvi članovi manji od 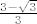 , lako pokažeš da je upravo to gornja granica. , lako pokažeš da je upravo to gornja granica.
Sad kad je dokazano da je niz konvergentan, odrediš limes zapravo na isti način na koji si određivao gornju granicu, rješavanjem one gore kvadratne jednadžbe. Rješenja joj znaš, tako da si zapravo gotov. 
Limes ti je isti kao i gornja granica (očito ne može biti onaj veći broj). Dakle, 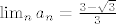 . Nadam se da je sve jasno i da nisam nešto fulao. . Nadam se da je sve jasno i da nisam nešto fulao. 
|
|
| [Vrh] |
|
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
Lanek_
Forumaš(ica)

Pridružen/a: 22. 10. 2010. (18:51:42)
Postovi: (31)16
|
|
| [Vrh] |
|
Dofalol
Forumaš(ica)

Pridružen/a: 24. 10. 2010. (21:25:31)
Postovi: (15)16
Spol: 
|
 Postano: 15:10 čet, 6. 1. 2011 Naslov: Postano: 15:10 čet, 6. 1. 2011 Naslov: |
    |
|
|
Nisam siguran točno kaj te muči pa ću probati još jednom objasniti...
Pretpostavka indukcije mi je da [latex]a_{k+2} \geq a_{k+1} \geq a_k[/latex].
Korak mi ide tako da koristim tu pretpostavku i dobijem da je [latex]a_{k+3} \geq a_{k+2}[/latex].
Znači, dokazao sam u koraku da ako mi niz ima tri uzastopna člana u rastućem poretku, onda će mu i onaj član odmah nakon ta tri biti veći ili jednak od njih. Kada uzmem u obzir koja mi je baza, dobijem da mi uvijek vrijedi da je [latex]a_{n+1} \geq a_n[/latex], odnosno da je niz rastući.
I da, takav dokaz je dobar. Čista matematička indukcija.
Nadam se da je sad ok. :)
Nisam siguran točno kaj te muči pa ću probati još jednom objasniti...
Pretpostavka indukcije mi je da 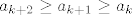 . .
Korak mi ide tako da koristim tu pretpostavku i dobijem da je 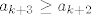 . .
Znači, dokazao sam u koraku da ako mi niz ima tri uzastopna člana u rastućem poretku, onda će mu i onaj član odmah nakon ta tri biti veći ili jednak od njih. Kada uzmem u obzir koja mi je baza, dobijem da mi uvijek vrijedi da je 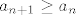 , odnosno da je niz rastući. , odnosno da je niz rastući.
I da, takav dokaz je dobar. Čista matematička indukcija.
Nadam se da je sad ok. 
|
|
| [Vrh] |
|
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
 Postano: 22:21 čet, 6. 1. 2011 Naslov: Postano: 22:21 čet, 6. 1. 2011 Naslov: |
    |
|
|
[quote="Lanek_"][quote="Dofalol"]
Činjenicu da je rastući pokažeš indukcijom.
Za bazu uzmeš [latex]a_3 = \frac13 \geq a_2= 0 \geq a_1 = 0[/latex].
Korak indukcije ti ide na foru da ako je [latex]a_{k+2} \geq a_{k+1} \geq a_k[/latex], onda je [latex]a_{k+3} = \frac12a_{k+2}a_{k+1}+\frac13 \geq \frac12a_{k+1}a_k+\frac13 = a_{k+2}[/latex]. Možda je malo čudnija indukcija nego inače, ali ništa strašno...
[/quote]
pa jel to dovoljno napisati za dokaz? mislim kako se iz koraka vidi da smo dokazali da je niz rastuci???
mozda jer smo koristili pret da je [latex]a_{n+1}\geq a_{n+2}??[/latex]
pa onda u koraku mora lijeva strana biti veća od desne baš radi tih članova? ak razumijes na kaj ciljam[/quote]
Pretpostavka se oslanja na istinitost baze, a baza vrijedi. Zato smijes pretpostaviti da vrijedi pretpostavka, jer stvarno vrijedi za neke clanove niza. Dakle, korak je valjan
| Lanek_ (napisa): | | Dofalol (napisa): |
Činjenicu da je rastući pokažeš indukcijom.
Za bazu uzmeš 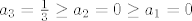 . .
Korak indukcije ti ide na foru da ako je 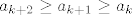 , onda je , onda je 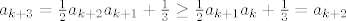 . Možda je malo čudnija indukcija nego inače, ali ništa strašno... . Možda je malo čudnija indukcija nego inače, ali ništa strašno...
|
pa jel to dovoljno napisati za dokaz? mislim kako se iz koraka vidi da smo dokazali da je niz rastuci???
mozda jer smo koristili pret da je 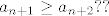
pa onda u koraku mora lijeva strana biti veća od desne baš radi tih članova? ak razumijes na kaj ciljam |
Pretpostavka se oslanja na istinitost baze, a baza vrijedi. Zato smijes pretpostaviti da vrijedi pretpostavka, jer stvarno vrijedi za neke clanove niza. Dakle, korak je valjan
|
|
| [Vrh] |
|
888
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (18:26:14)
Postovi: (29)16
|
|
| [Vrh] |
|
shimija
Forumaš(ica)


Pridružen/a: 22. 01. 2007. (18:33:54)
Postovi: (138)16
Spol: 
Lokacija: Spljit
|
|
| [Vrh] |
|
sstudentica
Forumaš(ica)
Pridružen/a: 30. 11. 2010. (13:18:02)
Postovi: (3A)16
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
 Postano: 18:34 ned, 9. 1. 2011 Naslov: Postano: 18:34 ned, 9. 1. 2011 Naslov: |
    |
|
|
[quote="sstudentica"]da li moze netko rijesiti s proslogodisnjeg kolokvija prvi zadatak??? bas taj...[/quote]
[latex]a_{n+2}=a^2_{n+1}+\frac{1}{6}a_{n}+\frac{1}{9}[/latex]
Da pokazemo da je niz konvergentan, trebamo dokazati ogranicenost i monotonst.
Pretpostavimo da postoji limes pa cemo umjesto clanova niza u niz uvrstiti L.
[latex]L=L^2+\frac{1}{6}L+\frac{1}{9} \Rightarrow L=\frac{1}{6} \;, L=\frac{1}{9}[/latex]
Iako imamo dvije vrijednost, probat cemo s manjom. Ako ta ne stima, onda uzimas ovu drugu.
Dokaz monotonosti indukcijom:
baza: [latex]a_{1}=0 \leqslant a_{2}=0 \\
a_{2}<a_{3}=\frac{1}{9}[/latex]
pretpostvka: vrijedi za neki n prirodan broj
[latex]a_{n+1}\leqslant a_{n+2}[/latex]
korak: iskoristavamo pretpostavku
[latex]a_{n+2}\leqslant a_{n+3}\\
a_{n+1}^2+\frac{1}{6}a_{n}+\frac{1}{9} \leqslant a_{n+2}^2+\frac{1}{6}a_{n+1}+\frac{1}{9}[/latex]
Po pretpostavci, monotonost vrijedi za svaki n prirodan broj.
Na slican nacin probaj sama dokazati omedenost t.d. pretpostavis
[latex]a_{n+1}\leqslant\frac{1}{6} [/latex], u koraku uvrstis [latex]\frac{1}{6}[/latex] i vidjet ces da je niz omeden i monoton pa znamo da je i konvergentan.
| sstudentica (napisa): | | da li moze netko rijesiti s proslogodisnjeg kolokvija prvi zadatak??? bas taj... |
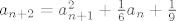
Da pokazemo da je niz konvergentan, trebamo dokazati ogranicenost i monotonst.
Pretpostavimo da postoji limes pa cemo umjesto clanova niza u niz uvrstiti L.
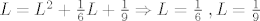
Iako imamo dvije vrijednost, probat cemo s manjom. Ako ta ne stima, onda uzimas ovu drugu.
Dokaz monotonosti indukcijom:
baza: 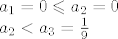
pretpostvka: vrijedi za neki n prirodan broj
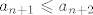
korak: iskoristavamo pretpostavku
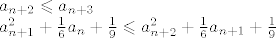
Po pretpostavci, monotonost vrijedi za svaki n prirodan broj.
Na slican nacin probaj sama dokazati omedenost t.d. pretpostavis
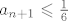 , u koraku uvrstis , u koraku uvrstis  i vidjet ces da je niz omeden i monoton pa znamo da je i konvergentan. i vidjet ces da je niz omeden i monoton pa znamo da je i konvergentan.
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
 Postano: 19:17 ned, 9. 1. 2011 Naslov: Postano: 19:17 ned, 9. 1. 2011 Naslov: |
    |
|
|
Evo rijesit cu iz 1. grupe, zadatak glasi:
Pokazati da je zadani niz konvergentan i odrediti mu limes,
[latex]a_{n+2} = a_{n+1}^2 + \displaystyle\frac{1}{6}a_n + \displaystyle\frac{1}{9}[/latex]
Krenimo od monotonosti, standardna indukcija:
[latex]a_1 \leq a_2 \leq a_3 = \frac{1}{9}[/latex]
pretpostavimo da za neki n vrijedi [latex]a_{n-1} \leq a_n \leq a_{n+1}[/latex] i dokazimo da to implicira [latex]a_{n+1} \leq a_{n+2} \Leftrightarrow a_n^2 + \displaystyle\frac{1}{6}a_{n-1} + \displaystyle\frac{1}{9} \leq a_{n+1}^2 + \displaystyle\frac{1}{6}a_n + \displaystyle\frac{1}{9} \Leftrightarrow a_{n}^2 + \displaystyle\frac{1}{6}a_{n-1} \leq a_{n+1}^2 + \displaystyle\frac{1}{6}a_{n}[/latex]
danu nejednakost razbijmo na ovakav sustav:
[latex]a_{n+1}^2 \geq a_n^2 \qquad (1) \\ \\
\displaystyle\frac{1}{6}a_{n} \geq \displaystyle\frac{1}{6}a_{n-1} \qquad (2)[/latex]
Dok je [latex](2)[/latex] trivijalna posljedica pretpostavke indukcije, [latex](1)[/latex] to nije. Naime, potrebna nam je nenegativnost niza (razlog tomu je sto je preslikvanje [latex]x \mapsto x^2[/latex] strogo rastuce na [latex]\left[0,+\infty \rangle[/latex], ali ne na [latex]\mathbb{R}[/latex]). Primjetimo da sada dokazom nenegativnosti kompletiramo dokaz monotonosti.
Ukoliko promatramo rekurzivni izraz kojim je niz zadan, primjetimo da [latex]a_n \geq 0 \implies a_{n+2} \geq 0[/latex]. Sad je indukcija jednostavna: [latex]a_1 = a_2 = 0[/latex], pretp. [latex]a_n \geq 0, a_{n+1} \geq 0 \implies a_{n+2} \geq 0[/latex].
Ogranicenost mozemo dobiti tako da unaprijed izracunamo limes i onda pogledamo koja bi nam bila dobra gornja medja. Imamo:
[latex]L = L^2 + \displaystyle\frac{1}{6} L + \displaystyle\frac{1}{9} \implies L_1 = \displaystyle\frac{2}{3}, \quad L_2 = \displaystyle\frac{1}{6}[/latex].
Sad indukcijom pokazemo da je [latex]a_n \leq L_2, n\in\mathbb{N}[/latex]. Prije nego sto to ucinim, samo bi valjalo komentirati da smo ogranicenost mogli dokazati s bilo kojom gornjom medjom iz [latex]\left[L_2, +\infty\rangle[/latex] , ali preferiramo gornje medje iz [latex]\left[L_2, L_1 \rangle[/latex] jer smo time automatski eliminirali kandidata za limes.
[latex]a_1 = a_2 \leq \displaystyle\frac{1}{6}[/latex]
Pretpostavimo: [latex]a_{n} \leq a_{n+1} \leq \displaystyle\frac{1}{6}[/latex]
Sad imamo:
[latex]a_{n+2} = a_{n+1}^2 + \displaystyle\frac{1}{6}a_n +\displaystyle\frac{1}{9} \leq \displaystyle\frac{1}{36} + \displaystyle\frac{1}{36} + \displaystyle\frac{1}{9} = \displaystyle\frac{1}{6}[/latex]
I time smo dovrsili dokaz da je zadani niz konvergentan s limesom [latex]\displaystyle\frac{1}{6}[/latex]. :)
EDIT: kolegica A-tom me je pretekla s postom dok sam pisao svoj (stvarno bih trebao poceti vjezbati malo brzinu :D ), ali opet, nece ni moj post smetati buduci da je kolegica samo skicirala rjesenje :)
Evo rijesit cu iz 1. grupe, zadatak glasi:
Pokazati da je zadani niz konvergentan i odrediti mu limes,
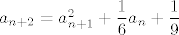
Krenimo od monotonosti, standardna indukcija:
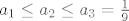
pretpostavimo da za neki n vrijedi 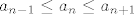 i dokazimo da to implicira i dokazimo da to implicira 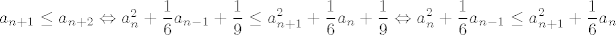
danu nejednakost razbijmo na ovakav sustav:
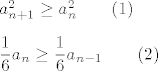
Dok je 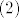 trivijalna posljedica pretpostavke indukcije, trivijalna posljedica pretpostavke indukcije, 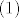 to nije. Naime, potrebna nam je nenegativnost niza (razlog tomu je sto je preslikvanje to nije. Naime, potrebna nam je nenegativnost niza (razlog tomu je sto je preslikvanje 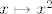 strogo rastuce na strogo rastuce na 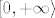 , ali ne na , ali ne na  ). Primjetimo da sada dokazom nenegativnosti kompletiramo dokaz monotonosti. ). Primjetimo da sada dokazom nenegativnosti kompletiramo dokaz monotonosti.
Ukoliko promatramo rekurzivni izraz kojim je niz zadan, primjetimo da  . Sad je indukcija jednostavna: . Sad je indukcija jednostavna: 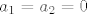 , pretp. , pretp. 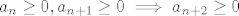 . .
Ogranicenost mozemo dobiti tako da unaprijed izracunamo limes i onda pogledamo koja bi nam bila dobra gornja medja. Imamo:
 . .
Sad indukcijom pokazemo da je 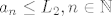 . Prije nego sto to ucinim, samo bi valjalo komentirati da smo ogranicenost mogli dokazati s bilo kojom gornjom medjom iz . Prije nego sto to ucinim, samo bi valjalo komentirati da smo ogranicenost mogli dokazati s bilo kojom gornjom medjom iz 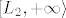 , ali preferiramo gornje medje iz , ali preferiramo gornje medje iz 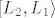 jer smo time automatski eliminirali kandidata za limes. jer smo time automatski eliminirali kandidata za limes.
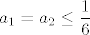
Pretpostavimo: 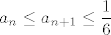
Sad imamo:
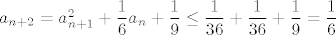
I time smo dovrsili dokaz da je zadani niz konvergentan s limesom  . . 
EDIT: kolegica A-tom me je pretekla s postom dok sam pisao svoj (stvarno bih trebao poceti vjezbati malo brzinu  ), ali opet, nece ni moj post smetati buduci da je kolegica samo skicirala rjesenje ), ali opet, nece ni moj post smetati buduci da je kolegica samo skicirala rjesenje 
|
|
| [Vrh] |
|
Joker
Forumaš(ica)

Pridružen/a: 19. 09. 2010. (10:19:16)
Postovi: (8C)16
Spol: 
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
 Postano: 20:26 ned, 9. 1. 2011 Naslov: Postano: 20:26 ned, 9. 1. 2011 Naslov: |
    |
|
|
Za svaki nikako jer to zelimo dokazati :D
ali moguca je varijanta da pretpostavimo da [latex](\exists n\in\mathbb{N}) (\forall k\in\mathbb{N}) (k \leq n \implies a_k \leq a_{k+1})[/latex], i to u sustini znaci da smo pretpostavili monotonost niza do neke tocke, odnosno [latex]a_1 \leq a_2 \leq \ldots \leq a_{n+1}[/latex], ali moja pretpostavka u ovom slucaju nije nista slabija, naime dokazom koraka indukcije, dobivam iduce:
[latex]a_1 \leq a_2 \leq a_3 \implies a_2 \leq a_3 \leq a_4 \implies \ldots \implies \\ a_n \leq a_{n+1} \leq a_{n+2} \implies a_{n+1} \leq a_{n+2} \leq a_{n+3} \implies\ldots[/latex]
odnosno dobivam monotonost cijelog niza koristeci cijelo vrijeme samo monotonost na segmentu niza od 3 elementa, sto nam pri samom dokazu koraka ustvari jedino i treba.
Pretpostavku mozemo postaviti bilo kako dok god cemo tako "pokriti" cijeli [latex]\mathbb{N}[/latex].
Za svaki nikako jer to zelimo dokazati 
ali moguca je varijanta da pretpostavimo da 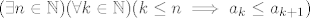 , i to u sustini znaci da smo pretpostavili monotonost niza do neke tocke, odnosno , i to u sustini znaci da smo pretpostavili monotonost niza do neke tocke, odnosno 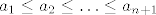 , ali moja pretpostavka u ovom slucaju nije nista slabija, naime dokazom koraka indukcije, dobivam iduce: , ali moja pretpostavka u ovom slucaju nije nista slabija, naime dokazom koraka indukcije, dobivam iduce:
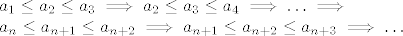
odnosno dobivam monotonost cijelog niza koristeci cijelo vrijeme samo monotonost na segmentu niza od 3 elementa, sto nam pri samom dokazu koraka ustvari jedino i treba.
Pretpostavku mozemo postaviti bilo kako dok god cemo tako "pokriti" cijeli 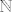 . .
|
|
| [Vrh] |
|
|













