| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 20:17 sri, 5. 1. 2011 Naslov: teorija Postano: 20:17 sri, 5. 1. 2011 Naslov: teorija |
    |
|
|
http://web.math.hr/nastava/difraf/dif/p_o15.pdf
na početku str.56, kod dokaza tm15.5,bi li mi mogao netko objasniti ovo nakon "pa je" pa do kraja, kako što iz čega slijedi,nije mi jasno baš..
i dokazati korolar 15.9 i napomenu 15.11. (ukoliko nije preteško,tj.toliko teško da se neće pojaviti na kolokviju pa zato ima zvjezdicu :D )?
http://web.math.hr/nastava/difraf/dif/p_o17.pdf
i teorem 17.1, tu mi ništa nije jasno osim prve rečenice :(
http://web.math.hr/nastava/difraf/dif/p_o15.pdf
na početku str.56, kod dokaza tm15.5,bi li mi mogao netko objasniti ovo nakon "pa je" pa do kraja, kako što iz čega slijedi,nije mi jasno baš..
i dokazati korolar 15.9 i napomenu 15.11. (ukoliko nije preteško,tj.toliko teško da se neće pojaviti na kolokviju pa zato ima zvjezdicu  )? )?
http://web.math.hr/nastava/difraf/dif/p_o17.pdf
i teorem 17.1, tu mi ništa nije jasno osim prve rečenice 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 22:43 sri, 5. 1. 2011 Naslov: Postano: 22:43 sri, 5. 1. 2011 Naslov: |
    |
|
|
15.5 Prvo se koristi [latex]\displaystyle Df(c)e_i = \frac{\partial f}{\partial x_i}(c)[/latex]. Treći izraz se dobi iz drugog iz definicije parcijalne derivacije.
15.9 Indukcijom. [latex]f[/latex] i [latex]g[/latex] su klase [latex]C^k[/latex] => [latex]Df(c)[/latex] i [latex]Dg(f(c))[/latex] su klase [latex]C^{k - 1}[/latex] => [latex]D(g \circ f)(c) = Dg(f(c)) Df(c)[/latex] je klase [latex]C^{k - 1}[/latex] => [latex]g \circ f[/latex] je klase [latex]C^k[/latex].
15.11 U dokaz Schwartzovog teorema se dobije pri kraju [latex]\displaystyle \frac{\partial f}{\partial y \partial x}(c_{h, k}, d_{h, k}) = \frac{\partial f}{\partial x \partial y}(\bar{c}_{h, k}, \bar{d}_{h, k})[/latex]. Pusti se limes i dobije se tvrdnja teorema. Ako samo pretpostavimo da postoji i neprekidna je jedna od parcijalnih derivacija, iz te jednakosti slijedi egzistencija i neprekidnost druge.
17.1 Znamo otprije da je [latex]{\sf grad} \, g[/latex] okomit na plohu S. Bilo bi zgodno pokazati da isto vrijedi i za [latex]{\sf grad} \, f[/latex]. Iz toga odmah slijedi da su ta dva gradijenta kolinearna. Ideja je pokazati da je [latex]{\sf grad} \, f[/latex] okomit na sve tangencijalne vektore, i to je sve što se radi u dokazu. Reci ako treba nešto preciznije objasniti.
15.5 Prvo se koristi 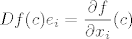 . Treći izraz se dobi iz drugog iz definicije parcijalne derivacije. . Treći izraz se dobi iz drugog iz definicije parcijalne derivacije.
15.9 Indukcijom.  i i  su klase su klase 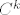 ⇒ ⇒ 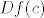 i i 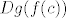 su klase su klase 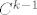 ⇒ ⇒ 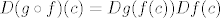 je klase je klase 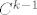 ⇒ ⇒ 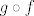 je klase je klase 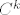 . .
15.11 U dokaz Schwartzovog teorema se dobije pri kraju 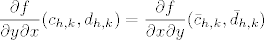 . Pusti se limes i dobije se tvrdnja teorema. Ako samo pretpostavimo da postoji i neprekidna je jedna od parcijalnih derivacija, iz te jednakosti slijedi egzistencija i neprekidnost druge. . Pusti se limes i dobije se tvrdnja teorema. Ako samo pretpostavimo da postoji i neprekidna je jedna od parcijalnih derivacija, iz te jednakosti slijedi egzistencija i neprekidnost druge.
17.1 Znamo otprije da je 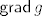 okomit na plohu S. Bilo bi zgodno pokazati da isto vrijedi i za okomit na plohu S. Bilo bi zgodno pokazati da isto vrijedi i za 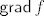 . Iz toga odmah slijedi da su ta dva gradijenta kolinearna. Ideja je pokazati da je . Iz toga odmah slijedi da su ta dva gradijenta kolinearna. Ideja je pokazati da je 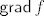 okomit na sve tangencijalne vektore, i to je sve što se radi u dokazu. Reci ako treba nešto preciznije objasniti. okomit na sve tangencijalne vektore, i to je sve što se radi u dokazu. Reci ako treba nešto preciznije objasniti.
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 10:05 čet, 6. 1. 2011 Naslov: Postano: 10:05 čet, 6. 1. 2011 Naslov: |
    |
|
|
[quote="pmli"]druge.
17.1 Znamo otprije da je [latex]{\sf grad} \, g[/latex] okomit na plohu S. Bilo bi zgodno pokazati da isto vrijedi i za [latex]{\sf grad} \, f[/latex]. Iz toga odmah slijedi da su ta dva gradijenta kolinearna. Ideja je pokazati da je [latex]{\sf grad} \, f[/latex] okomit na sve tangencijalne vektore, i to je sve što se radi u dokazu. Reci ako treba nešto preciznije objasniti.[/quote]
to mi je jasno,odnosno shvatila sam što želimo dokazati. nije mi jasno npr. "za svaki put c kroz x0 = c(0) vrijedi g(c(t)) = 0 -> d/dt(g(c(t)))"
što je put c, zašto je x0=c(0) (zašto baš c(0),i što to znači uopće), zašto je g(c(t))=0 i po čemu to povlači da je i derivacija toga jednaka 0?
onda,"S druge strane, ako je u x0 lokalni ekstrem funkcije f|S slijedi da je 0 lokalni ekstrem funkcije t → f(c(t))."
što je tu ta funkcija t → f(c(t)) i zašto vrijedi ta implikacija, i oovaj sljedeći izraz,jasno mi je da ako je ekstrem,da je derivacija =0, ali zašto ovo |t=0 u indexu?
i gdje smo vidjeli da vrijedi korolar 17.2?
to je za sada to(iako se nadam se drugog neće biti),idem proučavat ovo drugo što si mi napisao! :wink:
i puno ti hvala..
| pmli (napisa): | druge.
17.1 Znamo otprije da je 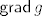 okomit na plohu S. Bilo bi zgodno pokazati da isto vrijedi i za okomit na plohu S. Bilo bi zgodno pokazati da isto vrijedi i za 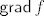 . Iz toga odmah slijedi da su ta dva gradijenta kolinearna. Ideja je pokazati da je . Iz toga odmah slijedi da su ta dva gradijenta kolinearna. Ideja je pokazati da je 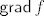 okomit na sve tangencijalne vektore, i to je sve što se radi u dokazu. Reci ako treba nešto preciznije objasniti. okomit na sve tangencijalne vektore, i to je sve što se radi u dokazu. Reci ako treba nešto preciznije objasniti. |
to mi je jasno,odnosno shvatila sam što želimo dokazati. nije mi jasno npr. "za svaki put c kroz x0 = c(0) vrijedi g(c(t)) = 0 → d/dt(g(c(t)))"
što je put c, zašto je x0=c(0) (zašto baš c(0),i što to znači uopće), zašto je g(c(t))=0 i po čemu to povlači da je i derivacija toga jednaka 0?
onda,"S druge strane, ako je u x0 lokalni ekstrem funkcije f|S slijedi da je 0 lokalni ekstrem funkcije t → f(c(t))."
što je tu ta funkcija t → f(c(t)) i zašto vrijedi ta implikacija, i oovaj sljedeći izraz,jasno mi je da ako je ekstrem,da je derivacija =0, ali zašto ovo |t=0 u indexu?
i gdje smo vidjeli da vrijedi korolar 17.2?
to je za sada to(iako se nadam se drugog neće biti),idem proučavat ovo drugo što si mi napisao! 
i puno ti hvala..
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 14:15 čet, 6. 1. 2011 Naslov: Postano: 14:15 čet, 6. 1. 2011 Naslov: |
    |
|
|
[quote=".anchy."]to mi je jasno,odnosno shvatila sam što želimo dokazati. nije mi jasno npr. "za svaki put c kroz x0 = c(0) vrijedi g(c(t)) = 0 -> d/dt(g(c(t)))"
što je put c[/quote]
Definirali smo što je put. To je neprekidna funkcija [latex]\alpha : [a, b] \to \mathbb{R}^k[/latex].
[quote=".anchy."]zašto je x0=c(0) (zašto baš c(0),i što to znači uopće)[/quote]
Ovdje smo je nazvali c jer se radi o krivulji (curve), tj. diferencijabilna je. Odabrali smo da je baš [latex]c(0) = x_0[/latex], a time ne gubimo na općenitosti.
[quote=".anchy."]zašto je g(c(t))=0[/quote]
Zato što smo odabrali da se krivulja c nalazi u plohi [latex]S = g^{-1}(\{0\})[/latex].
[quote=".anchy."]i po čemu to povlači da je i derivacija toga jednaka 0?[/quote]
Derivacija funkcije [latex]t \mapsto 0[/latex] (desna strana jednakosti) je opet isto to. :)
[quote=".anchy."]onda,"S druge strane, ako je u x0 lokalni ekstrem funkcije f|S slijedi da je 0 lokalni ekstrem funkcije t → f(c(t))."
što je tu ta funkcija t → f(c(t))[/quote]
Ta funkcija je nešto kao restrikcija funkcije f. Odabrali smo da c preslikava neke realne brojeve u neke elemente od S, koji je podskup od A (domena od f i g). Funkcija t → f(c(t)) je opet neka krivulja.
[quote=".anchy."]i zašto vrijedi ta implikacija[/quote]
Vrijedi [latex]f(c(0)) = f(x_0)[/latex]. Ako je [latex]x_0[/latex] lokalni ekstrem od [latex]f|_S[/latex], onda postoji neka okolina od [latex]x_0[/latex] koja je podskup od S na kojoj je [latex]f(x_0)[/latex] ekstremna vrijednost. No, krivulja c prolazi prolazi kroz tu okolinu, pa je [latex]f(x_0)[/latex] isto lokalno ekstremna vrijednost za funkciju t → f(c(t)).
[quote=".anchy."]i ovaj sljedeći izraz,jasno mi je da ako je ekstrem,da je derivacija =0, ali zašto ovo |t=0 u indexu?[/quote]
Ta oznaka znači uvrštavanje. Znači, prvo se derivira, onda se uvrsti t=0. (Derivacija je funkcija, pa tek kad ona djeluje na nešto, dobiš broj ;))
[quote=".anchy."]i gdje smo vidjeli da vrijedi korolar 17.2?[/quote]
Iz [latex]({\sf grad} \, f(x_0) | c'(0)) = 0[/latex]. Taj vektor je okomit na sve tangencijalne vektore, pa je okomit i na tangencijalnu ravninu.
| .anchy. (napisa): | to mi je jasno,odnosno shvatila sam što želimo dokazati. nije mi jasno npr. "za svaki put c kroz x0 = c(0) vrijedi g(c(t)) = 0 → d/dt(g(c(t)))"
što je put c |
Definirali smo što je put. To je neprekidna funkcija 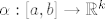 . .
| .anchy. (napisa): | | zašto je x0=c(0) (zašto baš c(0),i što to znači uopće) |
Ovdje smo je nazvali c jer se radi o krivulji (curve), tj. diferencijabilna je. Odabrali smo da je baš 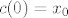 , a time ne gubimo na općenitosti. , a time ne gubimo na općenitosti.
| .anchy. (napisa): | | zašto je g(c(t))=0 |
Zato što smo odabrali da se krivulja c nalazi u plohi 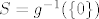 . .
| .anchy. (napisa): | | i po čemu to povlači da je i derivacija toga jednaka 0? |
Derivacija funkcije 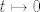 (desna strana jednakosti) je opet isto to. (desna strana jednakosti) je opet isto to. 
| .anchy. (napisa): | onda,"S druge strane, ako je u x0 lokalni ekstrem funkcije f|S slijedi da je 0 lokalni ekstrem funkcije t → f(c(t))."
što je tu ta funkcija t → f(c(t)) |
Ta funkcija je nešto kao restrikcija funkcije f. Odabrali smo da c preslikava neke realne brojeve u neke elemente od S, koji je podskup od A (domena od f i g). Funkcija t → f(c(t)) je opet neka krivulja.
| .anchy. (napisa): | | i zašto vrijedi ta implikacija |
Vrijedi 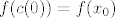 . Ako je . Ako je  lokalni ekstrem od lokalni ekstrem od 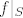 , onda postoji neka okolina od , onda postoji neka okolina od  koja je podskup od S na kojoj je koja je podskup od S na kojoj je 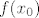 ekstremna vrijednost. No, krivulja c prolazi prolazi kroz tu okolinu, pa je ekstremna vrijednost. No, krivulja c prolazi prolazi kroz tu okolinu, pa je 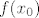 isto lokalno ekstremna vrijednost za funkciju t → f(c(t)). isto lokalno ekstremna vrijednost za funkciju t → f(c(t)).
| .anchy. (napisa): | | i ovaj sljedeći izraz,jasno mi je da ako je ekstrem,da je derivacija =0, ali zašto ovo |t=0 u indexu? |
Ta oznaka znači uvrštavanje. Znači, prvo se derivira, onda se uvrsti t=0. (Derivacija je funkcija, pa tek kad ona djeluje na nešto, dobiš broj  ) )
| .anchy. (napisa): | | i gdje smo vidjeli da vrijedi korolar 17.2? |
Iz 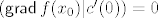 . Taj vektor je okomit na sve tangencijalne vektore, pa je okomit i na tangencijalnu ravninu. . Taj vektor je okomit na sve tangencijalne vektore, pa je okomit i na tangencijalnu ravninu.
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
|






