| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
Gea_
Forumaš(ica)

Pridružen/a: 04. 12. 2010. (00:31:15)
Postovi: (12)16
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
Togepi
Forumaš(ica)
Pridružen/a: 21. 11. 2010. (14:31:41)
Postovi: (2B)16
|
|
| [Vrh] |
|
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
 Postano: 12:05 čet, 13. 1. 2011 Naslov: Postano: 12:05 čet, 13. 1. 2011 Naslov: |
    |
|
|
[quote="Togepi"]Ah, ta ekvipotentnost.
Može netko formalno raspisat dokaz da skup N i N\{1, 2, 3} imaju jednako elemenata?[/quote]
samo stavis f:N->N\{1,2,3}
f(n)=n+3
uspostavis bijekciju izmedu ta dva skupa,ako se ne varam
| Togepi (napisa): | Ah, ta ekvipotentnost.
Može netko formalno raspisat dokaz da skup N i N\{1, 2, 3} imaju jednako elemenata? |
samo stavis f:N→N\{1,2,3}
f(n)=n+3
uspostavis bijekciju izmedu ta dva skupa,ako se ne varam
_________________
tko rano rani,malo spava
|
|
| [Vrh] |
|
Togepi
Forumaš(ica)
Pridružen/a: 21. 11. 2010. (14:31:41)
Postovi: (2B)16
|
|
| [Vrh] |
|
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
 Postano: 15:19 čet, 13. 1. 2011 Naslov: Postano: 15:19 čet, 13. 1. 2011 Naslov: |
    |
|
|
sad mi nije jasno kaj tocno trebas na kraju al recimo da je ovo zadatak
dokaz da skup N i N\{1, 2, 3} imaju jednako elemenata?
skup N ima beskonacno mnogo clanova...i sad ako mu oduzmes 3 i dalje ima beskonacno mnogo clanova,sad je dovoljno samo napravit takvu funkciju koja to potvrduje...i uzmemo f(n)=n+3 gdje je n prirodan broj
domena je N a kodomena N\{1,2,3} i sad uspostavimo bijekciju uzmedu ta dva skupa... to lako pokazemo da je ta funkcija bijekcija
i sad je to gotovo...
a definicija ekvipotentnosti,ako te to zbunjuje:
kažemo da su skupovi S i T(u našem slučaju N i N{1,2,3} ekvipotentni ako postoji bijekcija f:S->T(f:N->N{1,2,3})
sad mi nije jasno kaj tocno trebas na kraju al recimo da je ovo zadatak
dokaz da skup N i N\{1, 2, 3} imaju jednako elemenata?
skup N ima beskonacno mnogo clanova...i sad ako mu oduzmes 3 i dalje ima beskonacno mnogo clanova,sad je dovoljno samo napravit takvu funkciju koja to potvrduje...i uzmemo f(n)=n+3 gdje je n prirodan broj
domena je N a kodomena N\{1,2,3} i sad uspostavimo bijekciju uzmedu ta dva skupa... to lako pokazemo da je ta funkcija bijekcija
i sad je to gotovo...
a definicija ekvipotentnosti,ako te to zbunjuje:
kažemo da su skupovi S i T(u našem slučaju N i N{1,2,3} ekvipotentni ako postoji bijekcija f:S->T(f:N->N{1,2,3})
_________________
tko rano rani,malo spava
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
Buki
Forumaš(ica)

Pridružen/a: 17. 10. 2010. (20:15:17)
Postovi: (56)16
|
 Postano: 17:32 čet, 13. 1. 2011 Naslov: Postano: 17:32 čet, 13. 1. 2011 Naslov: |
    |
|
|
[quote="Tomislav"][quote="Togepi"]Hvala na odgovoru, ali nisam sigurna da li sam razumjela "do kraja". :oops: Što za dokaz da su N\{3}U{0}i N ekvipotentni?[/quote]
Neka je f(0)=1, f(1)=2, f(2)=3, f(n)=n za n>3.[/quote]
znaci li to da mozemo koristiti i funkcije koje nisu neprekidne, recimo:
za ekvipotentnost od N i N\{5} uzeti funkciju f(x)=
x ; za x<5
x+1 ; za x>=5
| Tomislav (napisa): | | Togepi (napisa): | Hvala na odgovoru, ali nisam sigurna da li sam razumjela "do kraja".  Što za dokaz da su N\{3}U{0}i N ekvipotentni? Što za dokaz da su N\{3}U{0}i N ekvipotentni? |
Neka je f(0)=1, f(1)=2, f(2)=3, f(n)=n za n>3. |
znaci li to da mozemo koristiti i funkcije koje nisu neprekidne, recimo:
za ekvipotentnost od N i N\{5} uzeti funkciju f(x)=
x ; za x<5
x+1 ; za x>=5
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 17:35 čet, 13. 1. 2011 Naslov: Postano: 17:35 čet, 13. 1. 2011 Naslov: |
    |
|
|
[quote="Buki"][quote="Tomislav"][quote="Togepi"]Hvala na odgovoru, ali nisam sigurna da li sam razumjela "do kraja". :oops: Što za dokaz da su N\{3}U{0}i N ekvipotentni?[/quote]
Neka je f(0)=1, f(1)=2, f(2)=3, f(n)=n za n>3.[/quote]
znaci li to da mozemo koristiti i funkcije koje nisu neprekidne, recimo:
za ekvipotentnost od N i N\{5} uzeti funkciju f(x)=
x ; za x<5
x+1 ; za x>=5[/quote]
Naravno :D Ovdje ni ne znam kakvog smisla ima neprekidnost kad funkcija ima domenu "rijedak" skup poput N. :D
| Buki (napisa): | | Tomislav (napisa): | | Togepi (napisa): | Hvala na odgovoru, ali nisam sigurna da li sam razumjela "do kraja".  Što za dokaz da su N\{3}U{0}i N ekvipotentni? Što za dokaz da su N\{3}U{0}i N ekvipotentni? |
Neka je f(0)=1, f(1)=2, f(2)=3, f(n)=n za n>3. |
znaci li to da mozemo koristiti i funkcije koje nisu neprekidne, recimo:
za ekvipotentnost od N i N\{5} uzeti funkciju f(x)=
x ; za x<5
x+1 ; za x>=5 |
Naravno  Ovdje ni ne znam kakvog smisla ima neprekidnost kad funkcija ima domenu "rijedak" skup poput N. Ovdje ni ne znam kakvog smisla ima neprekidnost kad funkcija ima domenu "rijedak" skup poput N. 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
Buki
Forumaš(ica)

Pridružen/a: 17. 10. 2010. (20:15:17)
Postovi: (56)16
|
|
| [Vrh] |
|
Togepi
Forumaš(ica)
Pridružen/a: 21. 11. 2010. (14:31:41)
Postovi: (2B)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
Togepi
Forumaš(ica)
Pridružen/a: 21. 11. 2010. (14:31:41)
Postovi: (2B)16
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 20:09 čet, 13. 1. 2011 Naslov: Postano: 20:09 čet, 13. 1. 2011 Naslov: |
    |
|
|
[quote="Tomislav"]Ja sam rijesio onaj u 1. grupi tako da sam faktorizirao:
[latex]f(x)=x^4 +2x^3 +5x^2 +4x+4=(x^2 +x+2)^2 [/latex][/quote]
Da, i ja sam tako, al ne znam sto svi kazu da moze preko derivacija, te derivacije jesu logicne kad se spomene visestruka nultocka (kratnost), al ja sam isla na foru, ako je barem jedna nultocka visestruka onda su moguci sljedeci slucajevi:
1) [ (x-a)^2 ]* [ (x-b)^2 ] ===> kad izbacimo kvadrat ispod ostane "neka" kvadratna jednadzba [ax^2 + bx + c] (dva put na kvadrat jer mora biti polinom 4.stupnja, )
2) (x-a)^3 * (x-b)
3) (x-a) * (x-b)^3
Ja sam prepotavila da je to prvi slucaj, preko teorema o jednakosti polinoma odrede se a,b,c, i to je to, i znao da kvadratna jednadzba ima 2 nultocke i obadvije ce biti kratnosti 2.
Nije mi jasno kako to preko derivacija rjesavate... :roll:
| Tomislav (napisa): | Ja sam rijesio onaj u 1. grupi tako da sam faktorizirao:
 |
Da, i ja sam tako, al ne znam sto svi kazu da moze preko derivacija, te derivacije jesu logicne kad se spomene visestruka nultocka (kratnost), al ja sam isla na foru, ako je barem jedna nultocka visestruka onda su moguci sljedeci slucajevi:
1) [ (x-a)^2 ]* [ (x-b)^2 ] ⇒ kad izbacimo kvadrat ispod ostane "neka" kvadratna jednadzba [ax^2 + bx + c] (dva put na kvadrat jer mora biti polinom 4.stupnja, )
2) (x-a)^3 * (x-b)
3) (x-a) * (x-b)^3
Ja sam prepotavila da je to prvi slucaj, preko teorema o jednakosti polinoma odrede se a,b,c, i to je to, i znao da kvadratna jednadzba ima 2 nultocke i obadvije ce biti kratnosti 2.
Nije mi jasno kako to preko derivacija rjesavate... 
|
|
| [Vrh] |
|
Ivanaa
Forumaš(ica)
Pridružen/a: 18. 10. 2010. (22:26:06)
Postovi: (35)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
 Postano: 20:18 čet, 13. 1. 2011 Naslov: Postano: 20:18 čet, 13. 1. 2011 Naslov: |
    |
|
|
[quote="frutabella"][quote="Tomislav"]Ja sam rijesio onaj u 1. grupi tako da sam faktorizirao:
[latex]f(x)=x^4 +2x^3 +5x^2 +4x+4=(x^2 +x+2)^2 [/latex][/quote]
Da, i ja sam tako, al ne znam sto svi kazu da moze preko derivacija, te derivacije jesu logicne kad se spomene visestruka nultocka (kratnost), al ja sam isla na foru, ako je barem jedna nultocka visestruka onda su moguci sljedeci slucajevi:
1) [ (x-a)^2 ]* [ (x-b)^2 ] ===> kad izbacimo kvadrat ispod ostane "neka" kvadratna jednadzba [ax^2 + bx + c] (dva put na kvadrat jer mora biti polinom 4.stupnja, )
2) (x-a)^3 * (x-b)
3) (x-a) * (x-b)^3
Ja sam prepotavila da je to prvi slucaj, preko teorema o jednakosti polinoma odrede se a,b,c, i to je to, i znao da kvadratna jednadzba ima 2 nultocke i obadvije ce biti kratnosti 2.
Nije mi jasno kako to preko derivacija rjesavate... :roll:[/quote]
Mozes takodjer i naci najveci zajednicu mjeru od f(x) i f'(x), pa ti rjesenje dode kao M(f(x),f'(x))=(x^2+x+2), pa je zadatak rijesen. :)
| frutabella (napisa): | | Tomislav (napisa): | Ja sam rijesio onaj u 1. grupi tako da sam faktorizirao:
 |
Da, i ja sam tako, al ne znam sto svi kazu da moze preko derivacija, te derivacije jesu logicne kad se spomene visestruka nultocka (kratnost), al ja sam isla na foru, ako je barem jedna nultocka visestruka onda su moguci sljedeci slucajevi:
1) [ (x-a)^2 ]* [ (x-b)^2 ] ⇒ kad izbacimo kvadrat ispod ostane "neka" kvadratna jednadzba [ax^2 + bx + c] (dva put na kvadrat jer mora biti polinom 4.stupnja, )
2) (x-a)^3 * (x-b)
3) (x-a) * (x-b)^3
Ja sam prepotavila da je to prvi slucaj, preko teorema o jednakosti polinoma odrede se a,b,c, i to je to, i znao da kvadratna jednadzba ima 2 nultocke i obadvije ce biti kratnosti 2.
Nije mi jasno kako to preko derivacija rjesavate...  |
Mozes takodjer i naci najveci zajednicu mjeru od f(x) i f'(x), pa ti rjesenje dode kao M(f(x),f'(x))=(x^2+x+2), pa je zadatak rijesen. 
|
|
| [Vrh] |
|
Bruno^_^
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (20:22:27)
Postovi: (1D)16
|
 Postano: 20:37 čet, 13. 1. 2011 Naslov: Postano: 20:37 čet, 13. 1. 2011 Naslov: |
    |
|
|
[quote]kak se dokaze da su [0,1] x [0,1] i [0,1] ekvipotentni skupovi [/quote]
treba dokazati da je card ([0,1] x [0,1]) = c
znaci treba naci bijekciju (x,y) i z, gdje su x,y, z e [0,1]
sada za x=0.x1x2x3x4x5... y=0.y1y2y3y4y5... definiras z=0.x1y1x2y1x3y3 itd
| Citat: | | kak se dokaze da su [0,1] x [0,1] i [0,1] ekvipotentni skupovi |
treba dokazati da je card ([0,1] x [0,1]) = c
znaci treba naci bijekciju (x,y) i z, gdje su x,y, z e [0,1]
sada za x=0.x1x2x3x4x5... y=0.y1y2y3y4y5... definiras z=0.x1y1x2y1x3y3 itd
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 20:44 čet, 13. 1. 2011 Naslov: Postano: 20:44 čet, 13. 1. 2011 Naslov: |
    |
|
|
[quote="pedro"]može pomoć oko ovih zadataka:
[b]1)[/b] dokažite da su [0,1] x [0,1] i [0,1] ekvipotentni skupovi
[b]2)[/b] Konstruirajte surjekciju s Q u N.
[b]3)[/b] Konstruirajte surjekciju s R u Q.
nije mi baš jasno ni kak da započnem zadatak. hvala[/quote]
1) Već odgovoreno. :)
2) [latex]f(x)=|\left\lfloor x\right\rfloor|+1[/latex]
3) [latex]f(x)=g(x)*x[/latex]
[latex]g(x)[/latex] je Dirichletova funkcija. Znači, ako je [latex]x[/latex] iracionalan, [latex]f(x)=0[/latex]. U protivnom, [latex]f(x)=x[/latex], i to je tražena surjekcija.
| pedro (napisa): | može pomoć oko ovih zadataka:
1) dokažite da su [0,1] x [0,1] i [0,1] ekvipotentni skupovi
2) Konstruirajte surjekciju s Q u N.
3) Konstruirajte surjekciju s R u Q.
nije mi baš jasno ni kak da započnem zadatak. hvala |
1) Već odgovoreno. 
2) 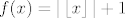
3) 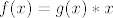
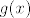 je Dirichletova funkcija. Znači, ako je je Dirichletova funkcija. Znači, ako je  iracionalan, iracionalan, 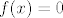 . U protivnom, . U protivnom, 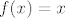 , i to je tražena surjekcija. , i to je tražena surjekcija.
|
|
| [Vrh] |
|
|











