| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Juraj Siftar
Gost
|
|
| [Vrh] |
|
Juraj Siftar
Gost
|
 Postano: 0:48 čet, 13. 1. 2011 Naslov: Postano: 0:48 čet, 13. 1. 2011 Naslov: |
    |
|
|
U vezi s geometrijskom i algebarskom kratnosti.
Prvo dobra vijest: ne morate znati taj dokaz da bi prošli ispit.
Onda loša vijest: ali trebate točno znati što su to geometrijska
i algebarska kratnost.
Sad, pod pretpostavkom da stvarno razumijete ta dva pojma, kako
ide dokaz.
Važno je da karakteristični polinom ne ovisi o matrici to jest bazi preko
kojeg ga računamo pa biramo onu bazu u kojoj će doći do izražaja
geometrijska kratnost: dakle, bazu koja sadrži bazu svojstvenog
potprostora (a ta baza ima vektora upravo koliko je geom. kratnost,
po definiciji).
Kad to učinimo, važno je razumijeti kako izgleda matrica operatora u
toj bazi: najprije imamo g stupaca (g neka je geom. kratnost) u
kojima po dijagonali ide dotična svojstvena vrijednost
(lambda_0 neka se zove),
a sve ostalo su nule (u tim stupcima) i još n-g stupaca za koje
ne možemo točno znati
kako izgledaju, a nije ni bitno.
Naime, determinanta matrice A - (lambda)I (u spomenutoj bazi)
očito ima faktor (lambda_0 - lambda) g puta
pa se u karakt. polinomu pojavljuje faktor (lambda_0 - lambda)^g.
Time je algebarska kratnost barem g, a jer se isti faktor možda još
pojavi i u preostalom dijelu determinante odnosno polinoma,
može biti i veća. No, iznosi najmanje g.
Eto, a vidio sam na konzultacijama da je u bilježnicama taj teorem
i dokaz super napisan pa nema prepreka da se tako super zna i na ispitu!
U vezi s geometrijskom i algebarskom kratnosti.
Prvo dobra vijest: ne morate znati taj dokaz da bi prošli ispit.
Onda loša vijest: ali trebate točno znati što su to geometrijska
i algebarska kratnost.
Sad, pod pretpostavkom da stvarno razumijete ta dva pojma, kako
ide dokaz.
Važno je da karakteristični polinom ne ovisi o matrici to jest bazi preko
kojeg ga računamo pa biramo onu bazu u kojoj će doći do izražaja
geometrijska kratnost: dakle, bazu koja sadrži bazu svojstvenog
potprostora (a ta baza ima vektora upravo koliko je geom. kratnost,
po definiciji).
Kad to učinimo, važno je razumijeti kako izgleda matrica operatora u
toj bazi: najprije imamo g stupaca (g neka je geom. kratnost) u
kojima po dijagonali ide dotična svojstvena vrijednost
(lambda_0 neka se zove),
a sve ostalo su nule (u tim stupcima) i još n-g stupaca za koje
ne možemo točno znati
kako izgledaju, a nije ni bitno.
Naime, determinanta matrice A - (lambda)I (u spomenutoj bazi)
očito ima faktor (lambda_0 - lambda) g puta
pa se u karakt. polinomu pojavljuje faktor (lambda_0 - lambda)^g.
Time je algebarska kratnost barem g, a jer se isti faktor možda još
pojavi i u preostalom dijelu determinante odnosno polinoma,
može biti i veća. No, iznosi najmanje g.
Eto, a vidio sam na konzultacijama da je u bilježnicama taj teorem
i dokaz super napisan pa nema prepreka da se tako super zna i na ispitu!
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Renči
Forumaš(ica)

Pridružen/a: 23. 09. 2009. (08:43:45)
Postovi: (5D)16
|
|
| [Vrh] |
|
gogo_
Forumaš(ica)

Pridružen/a: 07. 10. 2009. (17:06:47)
Postovi: (3F)16
|
|
| [Vrh] |
|
ante003
Forumaš(ica)


Pridružen/a: 13. 10. 2008. (17:45:10)
Postovi: (3C5)16
Spol: 
|
|
| [Vrh] |
|
Juraj Siftar
Gost
|
|
| [Vrh] |
|
gogo_
Forumaš(ica)

Pridružen/a: 07. 10. 2009. (17:06:47)
Postovi: (3F)16
|
|
| [Vrh] |
|
niky
Forumaš(ica)
Pridružen/a: 04. 11. 2008. (17:08:33)
Postovi: (2F)16
|
|
| [Vrh] |
|
gošća
Gost
|
|
| [Vrh] |
|
niky
Forumaš(ica)
Pridružen/a: 04. 11. 2008. (17:08:33)
Postovi: (2F)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
niky
Forumaš(ica)
Pridružen/a: 04. 11. 2008. (17:08:33)
Postovi: (2F)16
|
 Postano: 21:03 čet, 13. 1. 2011 Naslov: Postano: 21:03 čet, 13. 1. 2011 Naslov: |
    |
|
|
[quote="Anonymous"]Da li bi mi netko mogao riješiti zadatak: Nađi matricu operatora zrcaljenja na ravninu x+y-z=0 u kanonskoj bazi za V^3. Hvala[/quote]
Ja bi nasla vektore koje razapinju tu ravninu npr(1,0,1), (-1,-1,0). Onda primjenis formulu zrcaljenja s obzirom na ravninu zadanu s ta dva vektora.
Z(v)=v-2(n*x)n pri cemu je v=(x,y,z), n je vektor normale na ravninu razapetu s ta dva vektora, i onda nadjes operator Z cije stupce cine Z(i), Z(j), Z(k) ... Ako grijesim nek netko ispravi al ja bi to tako....
| Anonymous (napisa): | | Da li bi mi netko mogao riješiti zadatak: Nađi matricu operatora zrcaljenja na ravninu x+y-z=0 u kanonskoj bazi za V^3. Hvala |
Ja bi nasla vektore koje razapinju tu ravninu npr(1,0,1), (-1,-1,0). Onda primjenis formulu zrcaljenja s obzirom na ravninu zadanu s ta dva vektora.
Z(v)=v-2(n*x)n pri cemu je v=(x,y,z), n je vektor normale na ravninu razapetu s ta dva vektora, i onda nadjes operator Z cije stupce cine Z(i), Z(j), Z(k) ... Ako grijesim nek netko ispravi al ja bi to tako....
|
|
| [Vrh] |
|
Luka897
Gost
|
|
| [Vrh] |
|
ivana_1708
Forumaš(ica)

Pridružen/a: 01. 10. 2008. (08:19:58)
Postovi: (19)16
|
 Postano: 22:48 čet, 13. 1. 2011 Naslov: Postano: 22:48 čet, 13. 1. 2011 Naslov: |
    |
|
|
[quote="Luka897"]moze li netko rjesiti jedan zadatak sa rekurzijama iz 11. zadace samo da vidim kako se to rjesava. Hvala[/quote]
2. Zadatak iz 11. zadaće:
x_n+2 = -2x_n+1 + x_ n, n>=0.
Uvodimo trivijalno: x_n+1 = x_n+1
Rekurzivnu jednadžbu matrično zapisujemo kao: x_n+1 = A + x_n,
x_n = (x_n+1, x_n) (u matrici 2x1)
Iz toga slijedi da je matrica A={{-2, 1},{1,0}}.
Znamo da je x_n = A^n * x_0 = P * (lambda)^n* P^-1*x_0, gdje je (lambda)=dijagonalna matrica sa sv.vrijednostima od A na dijagonali, P je matrica prijelaza iz kanonske u bazu sv.vektora, a P^-1 možeš napisati kao i P^t ako ortonormiraš sv.vektore. x_0 = (0, -1) {početni uvjeti}.
Sad nađeš sv.vrijednosti i sv.vektore, uvrstiš u gornju formulu i na kraju dobiješ da je x_n = (-3/2)(-1 + 2sqrt2)^n + (-1/2)(-1 - 2sqrt2)^n.
Jednostavniji način je da ne računajući P zaključiš da x_n mora imati oblik x_n = (alfa)(lambda1)^n + (beta)(lambda2)^n. Imaš početne uvjetee koji ti kažu da je x_0 = -1, x_1 = 0. To uvrstiš u gornju formulu: x_0 = (alfa)(lambda1)^0 + (beta)(lambda2)^0, tako isto i za x_1. Dobiješ da je (alfa) = (-3/2), (beta) = (-1/2).
Nadam se da je jasno :)
| Luka897 (napisa): | | moze li netko rjesiti jedan zadatak sa rekurzijama iz 11. zadace samo da vidim kako se to rjesava. Hvala |
2. Zadatak iz 11. zadaće:
x_n+2 = -2x_n+1 + x_ n, n>=0.
Uvodimo trivijalno: x_n+1 = x_n+1
Rekurzivnu jednadžbu matrično zapisujemo kao: x_n+1 = A + x_n,
x_n = (x_n+1, x_n) (u matrici 2x1)
Iz toga slijedi da je matrica A={{-2, 1},{1,0}}.
Znamo da je x_n = A^n * x_0 = P * (lambda)^n* P^-1*x_0, gdje je (lambda)=dijagonalna matrica sa sv.vrijednostima od A na dijagonali, P je matrica prijelaza iz kanonske u bazu sv.vektora, a P^-1 možeš napisati kao i P^t ako ortonormiraš sv.vektore. x_0 = (0, -1) {početni uvjeti}.
Sad nađeš sv.vrijednosti i sv.vektore, uvrstiš u gornju formulu i na kraju dobiješ da je x_n = (-3/2)(-1 + 2sqrt2)^n + (-1/2)(-1 - 2sqrt2)^n.
Jednostavniji način je da ne računajući P zaključiš da x_n mora imati oblik x_n = (alfa)(lambda1)^n + (beta)(lambda2)^n. Imaš početne uvjetee koji ti kažu da je x_0 = -1, x_1 = 0. To uvrstiš u gornju formulu: x_0 = (alfa)(lambda1)^0 + (beta)(lambda2)^0, tako isto i za x_1. Dobiješ da je (alfa) = (-3/2), (beta) = (-1/2).
Nadam se da je jasno 
|
|
| [Vrh] |
|
ante003
Forumaš(ica)


Pridružen/a: 13. 10. 2008. (17:45:10)
Postovi: (3C5)16
Spol: 
|
|
| [Vrh] |
|
gogo_
Forumaš(ica)

Pridružen/a: 07. 10. 2009. (17:06:47)
Postovi: (3F)16
|
|
| [Vrh] |
|
ivana_1708
Forumaš(ica)

Pridružen/a: 01. 10. 2008. (08:19:58)
Postovi: (19)16
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)

Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol: 
|
 Postano: 0:08 pet, 14. 1. 2011 Naslov: Postano: 0:08 pet, 14. 1. 2011 Naslov: |
    |
|
|
[quote="ante003"][quote="Luka897"]moze li netko rjesiti jedan zadatak sa rekurzijama iz 11. zadace samo da vidim kako se to rjesava. Hvala[/quote]
Evo prvi. Necu ga prepisivat ovdje nego cu samo postupak napisat.
[latex]x_{n}=\left(\begin{array}{c}
x_{n}\\
y_{n}\end{array}\right)\\
x_{n+1}=\left(\begin{array}{cc}
\alpha_{1}& \beta_{1}\\
\alpha_{2}&\beta_{2}
\end{array}\right) *x_{n}=A*x_{n}\\
[/latex]
Onda matricu A iscitas iz zadatka i dode da je
[latex]\alpha_{1}=-1, \beta_{1}=-2, \alpha_{2}=-2, \beta_{2}=-1[/latex]
Tada, neka je [latex]x_{0}[/latex] matrica u kojoj su zapisani pocetni uvjeti i znamo da vrijedi ovo:
[latex]x_{n}=A^{n}*x_{0}[/latex] gdje je [latex]A^{n}[/latex] definirana ovako: [latex]A^{n}=P*\wedge^{n} * P^{-1}[/latex]. [b]Gdje je P matrica prijelaza iz (v) u (e) [/b]
Na kraju uneses izraz za [latex]A^{n}[/latex] u prvi izraz i dobijes par matrica koje moras pomnozit i na kraju samo procitat sto ti pise u njima. prvi red je rjesenje za [latex]x_{n}[/latex] a drugi za [latex]y_{n}[/latex]
[latex]x_{n}=P*\wedge^{n} *P^{-1}*x_{0}[/latex][/quote]
Ako se ja ne varam, onda se ti varas...Matrica P je matrica prijelaza iz (e) u (v), jer probaj to pomnozit...imas ovakve parove baza po tvojem...
(e,e)=(v,e)*(v,v)*(v,e)
dakle nije dobro...nego je matrica P matrica prijelaza iz (e) u (v), pa imas:
(e,e)=(e,v)*(v,v)*(e,v)
Sto se tice matrica prijelaza, opcenito(jer ovdje se to moze lijepo vidjeti po tome sto matrice moraju bit ulancane, pa svoje dileme mozemo rijesit uskladjivnjem ulancanosti):
Ako imas preslikavanje A: iz V u W, onda je jasno da kad uzmes jednu bazu za V i preslikas je u W, da su stupci te matrice A kandidati za sliku(u biti skup izvodnica za sliku), a isto tako i kandidati za bazu prostora W(iako naravno nemoraju biti, ali mogu, i sigurno se nalaze u prostoru W)
E sad, kad imas neku bazu (l) koja se sastoji od vektora l1,l2,...ln, i ako te vektore postavis u matricu kao stupce, i gledas tu matricu kao sto si gledao ovaj gore operator, onda je jasno da si presao u bazu (l)...tj. stupci matrice ti govore u kojoj si bazi...
| ante003 (napisa): | | Luka897 (napisa): | | moze li netko rjesiti jedan zadatak sa rekurzijama iz 11. zadace samo da vidim kako se to rjesava. Hvala |
Evo prvi. Necu ga prepisivat ovdje nego cu samo postupak napisat.
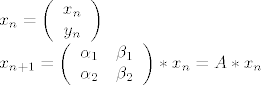
Onda matricu A iscitas iz zadatka i dode da je
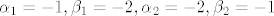
Tada, neka je 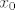 matrica u kojoj su zapisani pocetni uvjeti i znamo da vrijedi ovo: matrica u kojoj su zapisani pocetni uvjeti i znamo da vrijedi ovo:
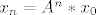 gdje je gdje je 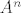 definirana ovako: definirana ovako: 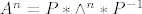 . Gdje je P matrica prijelaza iz (v) u (e) . Gdje je P matrica prijelaza iz (v) u (e)
Na kraju uneses izraz za 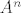 u prvi izraz i dobijes par matrica koje moras pomnozit i na kraju samo procitat sto ti pise u njima. prvi red je rjesenje za u prvi izraz i dobijes par matrica koje moras pomnozit i na kraju samo procitat sto ti pise u njima. prvi red je rjesenje za 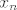 a drugi za a drugi za 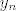
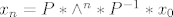 |
Ako se ja ne varam, onda se ti varas...Matrica P je matrica prijelaza iz (e) u (v), jer probaj to pomnozit...imas ovakve parove baza po tvojem...
(e,e)=(v,e)*(v,v)*(v,e)
dakle nije dobro...nego je matrica P matrica prijelaza iz (e) u (v), pa imas:
(e,e)=(e,v)*(v,v)*(e,v)
Sto se tice matrica prijelaza, opcenito(jer ovdje se to moze lijepo vidjeti po tome sto matrice moraju bit ulancane, pa svoje dileme mozemo rijesit uskladjivnjem ulancanosti):
Ako imas preslikavanje A: iz V u W, onda je jasno da kad uzmes jednu bazu za V i preslikas je u W, da su stupci te matrice A kandidati za sliku(u biti skup izvodnica za sliku), a isto tako i kandidati za bazu prostora W(iako naravno nemoraju biti, ali mogu, i sigurno se nalaze u prostoru W)
E sad, kad imas neku bazu (l) koja se sastoji od vektora l1,l2,...ln, i ako te vektore postavis u matricu kao stupce, i gledas tu matricu kao sto si gledao ovaj gore operator, onda je jasno da si presao u bazu (l)...tj. stupci matrice ti govore u kojoj si bazi...
|
|
| [Vrh] |
|
ante003
Forumaš(ica)


Pridružen/a: 13. 10. 2008. (17:45:10)
Postovi: (3C5)16
Spol: 
|
|
| [Vrh] |
|
|








