|
Udaljenost dvije točke može definirati kako god hoće ukoliko mu razdaljinska funkcija zadovoljava aksiome metrike.
No vjerojatno misli na induciranu (najčešće euklidsku) metriku koja je inducirana skalarnim produktom: ako je [latex](\cdot,\cdot)[/latex] skalarni produkt na unitarnom prostoru X, onda po Jordan-Von Neumannovom teoremu taj skalarni produkt inducira normu na X koja je dana sa [latex]|x|=\sqrt{(x,x)}[/latex], a ta norma inducira metriku koja je dana sa d(x,y)=|x-y|.
Nebitno je koliko dimenzija prostor ima, stvar vrijedi za sve (bes)konačne unitarne prostore.
Ako je potreban izvod formule za euklidsku udaljenost, to se svodi na primjenu Pitagorinog poučka i malo translacije, a trenutno mi se neda to raspisivati između ostalog zato što je ta tema dobro pokrivena na internetu. :)
EDIT: eto, ipak mi se da.[spoiler]Jednostavnosti radi, odrediti ćemo udaljenost neke točke (x1,y1,z1) od ishodišta (0,0,0) koordinatnog sustava pri čemu su x1,y1,z1>0. Ako točku (x1,y1,z1) projiciramo na ravninu određenu osima x i y, dobiti ćemo točku (x1,y1,0). Točke (0,0,0), (x1,y1,0) i (x1,y1,z1) čine pravokutan trokut s pravim kutem u točki (x1,y1,0). Nas zanima duljina hipotenuze tog trokuta.
Lako je vidjeti koja je duljina katete nasuprot ishodišta - ta duljina jednaka je z1. Duljinu preostale katete možemo izračunati Pitagorinim poučkom jer se točke (0,0,0) i (x1,y1,0) nalaze na istoj ravnini - ta duljina jednaka je [latex]\sqrt{x_1^2+y_1^2}[/latex].
Iz istog razloga i na isti način računamo duljinu hipotenuze: ta duljina biti će jednaka [latex]\sqrt{\left(\sqrt{x_1^2+y_1^2}\right)^2+z_1^2}=\sqrt{x_1^2+y_1^2+z_1^2}.[/latex]
Ono što preostaje napraviti je ponoviti račun kada umjesto ishodišta imamo neku točku (x2,y2,z2) - metoda računanja je ista, prvo se izračuna duljina katete koja je paralelna sa z osi, a zatim duljina preostale katete i nakraju duljina hipotenuze. Koordinate pravokutnog trokuta će biti nešto drugačije, ali ništa bitno kompliciranije.[/spoiler]
Udaljenost dvije točke može definirati kako god hoće ukoliko mu razdaljinska funkcija zadovoljava aksiome metrike.
No vjerojatno misli na induciranu (najčešće euklidsku) metriku koja je inducirana skalarnim produktom: ako je 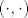 skalarni produkt na unitarnom prostoru X, onda po Jordan-Von Neumannovom teoremu taj skalarni produkt inducira normu na X koja je dana sa skalarni produkt na unitarnom prostoru X, onda po Jordan-Von Neumannovom teoremu taj skalarni produkt inducira normu na X koja je dana sa 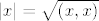 , a ta norma inducira metriku koja je dana sa d(x,y)=|x-y|. , a ta norma inducira metriku koja je dana sa d(x,y)=|x-y|.
Nebitno je koliko dimenzija prostor ima, stvar vrijedi za sve (bes)konačne unitarne prostore.
Ako je potreban izvod formule za euklidsku udaljenost, to se svodi na primjenu Pitagorinog poučka i malo translacije, a trenutno mi se neda to raspisivati između ostalog zato što je ta tema dobro pokrivena na internetu. 
EDIT: eto, ipak mi se da. | Spoiler [hidden; click to show]: | Jednostavnosti radi, odrediti ćemo udaljenost neke točke (x1,y1,z1) od ishodišta (0,0,0) koordinatnog sustava pri čemu su x1,y1,z1>0. Ako točku (x1,y1,z1) projiciramo na ravninu određenu osima x i y, dobiti ćemo točku (x1,y1,0). Točke (0,0,0), (x1,y1,0) i (x1,y1,z1) čine pravokutan trokut s pravim kutem u točki (x1,y1,0). Nas zanima duljina hipotenuze tog trokuta.
Lako je vidjeti koja je duljina katete nasuprot ishodišta - ta duljina jednaka je z1. Duljinu preostale katete možemo izračunati Pitagorinim poučkom jer se točke (0,0,0) i (x1,y1,0) nalaze na istoj ravnini - ta duljina jednaka je 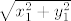 .
Iz istog razloga i na isti način računamo duljinu hipotenuze: ta duljina biti će jednaka 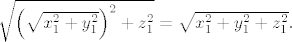
Ono što preostaje napraviti je ponoviti račun kada umjesto ishodišta imamo neku točku (x2,y2,z2) - metoda računanja je ista, prvo se izračuna duljina katete koja je paralelna sa z osi, a zatim duljina preostale katete i nakraju duljina hipotenuze. Koordinate pravokutnog trokuta će biti nešto drugačije, ali ništa bitno kompliciranije. |
_________________
The Dude Abides
|





