| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
654321
Forumaš(ica)

Pridružen/a: 18. 01. 2011. (18:30:01)
Postovi: (D)16
|
 Postano: 23:30 sri, 19. 1. 2011 Naslov: Zadatak iz kolokvija 2009 Postano: 23:30 sri, 19. 1. 2011 Naslov: Zadatak iz kolokvija 2009 |
    |
|
|
http://web.math.hr/nastava/la/kolokviji/08_09/kol2a.pdf
2. Zadatak
Kada napišem A u obliku a b c d
e f g h
i onda množenjem sa b i izjednačavanjem sa AB dođem do ovog djela neznam kako dalje....
Jel ovaj dobiveni izraz opet stavljam u matricu i rješavam a,b,c,d,e,f,g,h, ili nešto drugo???
-5a - 4b - 7c + d = 2
3a + 2b + 4c = -1
a - 2b + 2c + 3d = 2
a + b + c = -1
:
-5e - 4f - 7g + h = -9
3e + 2f + 4g = 5
e -2f + 2g + 3d = 2
e + f + g = 1
http://web.math.hr/nastava/la/kolokviji/08_09/kol2a.pdf
2. Zadatak
Kada napišem A u obliku a b c d
e f g h
i onda množenjem sa b i izjednačavanjem sa AB dođem do ovog djela neznam kako dalje....
Jel ovaj dobiveni izraz opet stavljam u matricu i rješavam a,b,c,d,e,f,g,h, ili nešto drugo???
-5a - 4b - 7c + d = 2
3a + 2b + 4c = -1
a - 2b + 2c + 3d = 2
a + b + c = -1
:
-5e - 4f - 7g + h = -9
3e + 2f + 4g = 5
e -2f + 2g + 3d = 2
e + f + g = 1
|
|
| [Vrh] |
|
rimidalv1991
Forumaš(ica)

Pridružen/a: 07. 07. 2009. (21:14:20)
Postovi: (22)16
|
 Postano: 23:40 sri, 19. 1. 2011 Naslov: Postano: 23:40 sri, 19. 1. 2011 Naslov: |
    |
|
|
Mozes to rjesiti tako da napravis dva sustava jednadzbi, jedan s a,b,c,d,, i jedan s e,f,g,h. Rjesis te sustave , i dobijes matricu A.
Mozes to rjesiti tako da napravis dva sustava jednadzbi, jedan s a,b,c,d,, i jedan s e,f,g,h. Rjesis te sustave , i dobijes matricu A.
|
|
| [Vrh] |
|
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
654321
Forumaš(ica)

Pridružen/a: 18. 01. 2011. (18:30:01)
Postovi: (D)16
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 0:25 čet, 20. 1. 2011 Naslov: Postano: 0:25 čet, 20. 1. 2011 Naslov: |
    |
|
|
[quote="654321"]@rimidalv1991
što to onda opet stavljam u matricu?
a onda nikako ne mogu dobit rješanja za a,b,c,d.
A što ako matrica nije regularna?[/quote]
A mozda da pokusas rjesiti sustav kako smo inace rjesavali, gaussovom metodom, ili opet stavi u matricu mozda pa ce ti a,b,c,d, biti isto kao da imas x1,x2,x3,x4, (ili koliko ih vec ima...), rjesis to kao sto se rjesavaju jednadzbe pomocu matrica i vidjet ces, da li je parametarsko, jedinstveno (u ovisnosti o rangu ---> n-r(A)= d)
Sad lupam napamet...probaj.
| 654321 (napisa): | @rimidalv1991
što to onda opet stavljam u matricu?
a onda nikako ne mogu dobit rješanja za a,b,c,d.
A što ako matrica nije regularna? |
A mozda da pokusas rjesiti sustav kako smo inace rjesavali, gaussovom metodom, ili opet stavi u matricu mozda pa ce ti a,b,c,d, biti isto kao da imas x1,x2,x3,x4, (ili koliko ih vec ima...), rjesis to kao sto se rjesavaju jednadzbe pomocu matrica i vidjet ces, da li je parametarsko, jedinstveno (u ovisnosti o rangu → n-r(A)= d)
Sad lupam napamet...probaj.
|
|
| [Vrh] |
|
CROmpir
Forumaš(ica)

Pridružen/a: 15. 09. 2009. (18:27:06)
Postovi: (B3)16
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
 Postano: 3:10 čet, 20. 1. 2011 Naslov: Postano: 3:10 čet, 20. 1. 2011 Naslov: |
    |
|
|
Problem mozemo rjesiti vrlo efikasno i elegantno bez raspisivanja sustava, ili trazenja inverza od B (kao sto je spomenuto, matrica B uopce ne mora imati inverz, mada sumnjam da bi takvo sta stavili u kolokvij, ali nikad se nezna :D ).
Radi preglednosti, uvedimo novu oznaku [latex]C[/latex] za matricu [latex]AB[/latex]. Sad imamo:
[latex]AB = C \Leftrightarrow A(BE_1 E_2 \ldots E_k) = CE_1 E_2 \ldots E_k[/latex]
gdje su [latex]E_i[/latex] elementarne matrice.
Ukoliko je [latex]BE_1 E_2 \ldots E_k = I[/latex], pronasli smo matricu [latex]A = CE_1 E_2 \ldots E_k[/latex].
Primjetimo da nam mnozenje elementarnim matricama zdesna predstavlja elementarne transformacije nad stupcima. Iz ovoga, slicno kao i kod Gauss - Jordana, dobivamo jednostavan algoritam za pronalazenje matrice [latex]A[/latex] - vrsimo elementarne transformacije nad stupcima prosirene matrice [latex](B | C)^t[/latex] dok ne dobijemo nesto oblika [latex](I | C')^t[/latex] pa iz toga zakljucujemo da je [latex]A = C'[/latex]. Naravno, stvari se pomalo kompliciraju ako [latex]B[/latex] nije regularan, ali onda mozemo rijesiti sustav parametarski, odnosno zakljuciti da rjesnje ne postoji.
[latex](B | C)^t[/latex] mi ustvari znaci da je [latex]C[/latex] "priljepljena" odozdo, a ne zdesna, kao sto je uobicajeno. Ukoliko vas takav nacin rjesavanja buni, uvijek mozete napraviti ovo:
[latex]AB = C \Leftrightarrow B^tA^t = C^t \Leftrightarrow (E_k \ldots E_2E_1B^t)A^t = E_k \ldots E_2E_1C^t[/latex] pa prosirenu matricu [latex](B^t | C^t)[/latex] zelimo dovesti u oblik [latex](I | C') \implies A^t = C' \implies A = (C')^t[/latex] (ukoliko je to moguce).
Na kraju jos da dodam kako neznam kolika korist ovog posta kad dolazi ovako kasno, pred kolokvij, ali eto, mozda nekome posluzi u buducnosti :)
Problem mozemo rjesiti vrlo efikasno i elegantno bez raspisivanja sustava, ili trazenja inverza od B (kao sto je spomenuto, matrica B uopce ne mora imati inverz, mada sumnjam da bi takvo sta stavili u kolokvij, ali nikad se nezna  ). ).
Radi preglednosti, uvedimo novu oznaku  za matricu za matricu 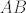 . Sad imamo: . Sad imamo:
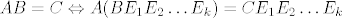
gdje su 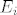 elementarne matrice. elementarne matrice.
Ukoliko je 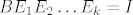 , pronasli smo matricu , pronasli smo matricu 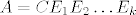 . .
Primjetimo da nam mnozenje elementarnim matricama zdesna predstavlja elementarne transformacije nad stupcima. Iz ovoga, slicno kao i kod Gauss - Jordana, dobivamo jednostavan algoritam za pronalazenje matrice  - vrsimo elementarne transformacije nad stupcima prosirene matrice - vrsimo elementarne transformacije nad stupcima prosirene matrice 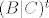 dok ne dobijemo nesto oblika dok ne dobijemo nesto oblika 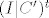 pa iz toga zakljucujemo da je pa iz toga zakljucujemo da je 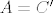 . Naravno, stvari se pomalo kompliciraju ako . Naravno, stvari se pomalo kompliciraju ako  nije regularan, ali onda mozemo rijesiti sustav parametarski, odnosno zakljuciti da rjesnje ne postoji. nije regularan, ali onda mozemo rijesiti sustav parametarski, odnosno zakljuciti da rjesnje ne postoji.
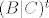 mi ustvari znaci da je mi ustvari znaci da je  "priljepljena" odozdo, a ne zdesna, kao sto je uobicajeno. Ukoliko vas takav nacin rjesavanja buni, uvijek mozete napraviti ovo: "priljepljena" odozdo, a ne zdesna, kao sto je uobicajeno. Ukoliko vas takav nacin rjesavanja buni, uvijek mozete napraviti ovo:
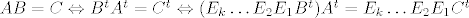 pa prosirenu matricu pa prosirenu matricu 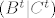 zelimo dovesti u oblik zelimo dovesti u oblik 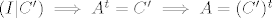 (ukoliko je to moguce). (ukoliko je to moguce).
Na kraju jos da dodam kako neznam kolika korist ovog posta kad dolazi ovako kasno, pred kolokvij, ali eto, mozda nekome posluzi u buducnosti 
|
|
| [Vrh] |
|
|





