| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 21:29 sub, 15. 1. 2011 Naslov: "Popravne" demonstrature Postano: 21:29 sub, 15. 1. 2011 Naslov: "Popravne" demonstrature |
    |
|
|
Dobra večer.
It has come to my attention da bi vjerojatno bilo štogod zainteresiranih za nekakvu formu demonstratura prije popravnog kolokvija iz MA1. Pa, dobro onda. :) Termin koji mi se čini dosta idealan (niti pripadajuće studentsko tijelo, niti ja, a možda niti potencijalni drugi demonstratori nemamo ništa pametnog za raditi u tom terminu, što se rasporeda kolokvija/usmenih tiče) bio bi ovaj petak: dakle, [b]petak, 21.1.2011. u 13 sati[/b]. Trajanje - u biti proizvoljno, dok god ljudi imaju pitanja. :)
E, sad, kako je to nekako moj sitan um zamislio. Dakle, rješavati zadatak po zadatak stare popravne kolokvije vjerojatno i nema smisla. Uostalom, na demonstraturama prije redovnih kolokvija provedemo par tjedana to radeći, a zadaci na popravnim kolokvijima (ili barem njihove ideje) su, esencijalno, kompilacija tih "redovnih" zadataka. Stoga, idealan bi bio sljedeći dijalog:
Trendafil: "Demonstratore, kućo stara. Ne znam riješiti ovaj zadatak, probao sam direktno izračunati infimum, od toga ništa, probao sam onda uvrstiti [latex]0[/latex], ali mi se papir zapalio. Što da radim i je li potrebno da žrtvujem ikakve životinje?"
Ja: [i][daje uobičajeno mudar i duhovit odgovor iz kojeg se vidi kako je to problem koji mori cijelu ispitanikovu generaciju, a žrtvovanje životinja je posve opcionalno - osobno, nisam veliki fan][/i]
Trendafil: "Vječna ti slava, demonstratore. Možeš li mi dati neku veću drvenu štapigu da se njome udarim po glavi?"
Dakle, ako niste shvatili: ako ste zainteresirani, 'ajde pripremite neka pitanja, neke dijelove gradiva koje baš ne razumijete do kraja ili sličan folklorni program. Bitno je da prije probate to sami sa sobom prije riješiti - budimo realni, to što ja (ili ja i još dva-tri-deset ljudi) s vama tamo odsjedim pola sata, sat, dva, šest sati, to vam neće samo po sebi osigurati da prođete popravni. Dapače, po mom skromnom mišljenju, neće vam ni uopće pomoći, ako samo sjedite tamo ([i]k'o, k'o, k'o pored kamenja[/i]... ako ima netko iz MIOC-a, ima šanse da shvaća :)) i gledate kako drugi maltretiraju demonstratora. Bitno je da ste prije demonstratura bili korisni, pa da sad hoćete da nešto prokomentiramo, a ne da počinjemo sve ispočetka.
Eto, to je bila obavijest - ljudi me uvjeravaju da zainteresiranih svakako ima, pa da i ostali znate. Još jednom, ako netko od demonstratora ima volju pomoći, super. :D Također, ako netko s prve godine zna MA1, a ima veselja i volje da pomogne drugovima, mislim da nitko ne bi imao ništa protiv. :) U svakom slučaju, što nas više, to bolje - brže riješimo pitanja. :)
(Inače, za udaranjem drvenom štapigom po glavi uistinu nikad nema potrebe, ako baš vas to personalno ne veseli - demonstratori služe da vam pomognu i ako nešto ne znate, znatno je mudrije sad doći i daviti koga već stignete da vam pomogne, nego daviti s istim pitanjima sljedeće godine. :))
Dobra večer.
It has come to my attention da bi vjerojatno bilo štogod zainteresiranih za nekakvu formu demonstratura prije popravnog kolokvija iz MA1. Pa, dobro onda.  Termin koji mi se čini dosta idealan (niti pripadajuće studentsko tijelo, niti ja, a možda niti potencijalni drugi demonstratori nemamo ništa pametnog za raditi u tom terminu, što se rasporeda kolokvija/usmenih tiče) bio bi ovaj petak: dakle, petak, 21.1.2011. u 13 sati. Trajanje - u biti proizvoljno, dok god ljudi imaju pitanja. Termin koji mi se čini dosta idealan (niti pripadajuće studentsko tijelo, niti ja, a možda niti potencijalni drugi demonstratori nemamo ništa pametnog za raditi u tom terminu, što se rasporeda kolokvija/usmenih tiče) bio bi ovaj petak: dakle, petak, 21.1.2011. u 13 sati. Trajanje - u biti proizvoljno, dok god ljudi imaju pitanja. 
E, sad, kako je to nekako moj sitan um zamislio. Dakle, rješavati zadatak po zadatak stare popravne kolokvije vjerojatno i nema smisla. Uostalom, na demonstraturama prije redovnih kolokvija provedemo par tjedana to radeći, a zadaci na popravnim kolokvijima (ili barem njihove ideje) su, esencijalno, kompilacija tih "redovnih" zadataka. Stoga, idealan bi bio sljedeći dijalog:
Trendafil: "Demonstratore, kućo stara. Ne znam riješiti ovaj zadatak, probao sam direktno izračunati infimum, od toga ništa, probao sam onda uvrstiti  , ali mi se papir zapalio. Što da radim i je li potrebno da žrtvujem ikakve životinje?" , ali mi se papir zapalio. Što da radim i je li potrebno da žrtvujem ikakve životinje?"
Ja: [daje uobičajeno mudar i duhovit odgovor iz kojeg se vidi kako je to problem koji mori cijelu ispitanikovu generaciju, a žrtvovanje životinja je posve opcionalno - osobno, nisam veliki fan]
Trendafil: "Vječna ti slava, demonstratore. Možeš li mi dati neku veću drvenu štapigu da se njome udarim po glavi?"
Dakle, ako niste shvatili: ako ste zainteresirani, 'ajde pripremite neka pitanja, neke dijelove gradiva koje baš ne razumijete do kraja ili sličan folklorni program. Bitno je da prije probate to sami sa sobom prije riješiti - budimo realni, to što ja (ili ja i još dva-tri-deset ljudi) s vama tamo odsjedim pola sata, sat, dva, šest sati, to vam neće samo po sebi osigurati da prođete popravni. Dapače, po mom skromnom mišljenju, neće vam ni uopće pomoći, ako samo sjedite tamo (k'o, k'o, k'o pored kamenja... ako ima netko iz MIOC-a, ima šanse da shvaća  ) i gledate kako drugi maltretiraju demonstratora. Bitno je da ste prije demonstratura bili korisni, pa da sad hoćete da nešto prokomentiramo, a ne da počinjemo sve ispočetka. ) i gledate kako drugi maltretiraju demonstratora. Bitno je da ste prije demonstratura bili korisni, pa da sad hoćete da nešto prokomentiramo, a ne da počinjemo sve ispočetka.
Eto, to je bila obavijest - ljudi me uvjeravaju da zainteresiranih svakako ima, pa da i ostali znate. Još jednom, ako netko od demonstratora ima volju pomoći, super.  Također, ako netko s prve godine zna MA1, a ima veselja i volje da pomogne drugovima, mislim da nitko ne bi imao ništa protiv. Također, ako netko s prve godine zna MA1, a ima veselja i volje da pomogne drugovima, mislim da nitko ne bi imao ništa protiv.  U svakom slučaju, što nas više, to bolje - brže riješimo pitanja. U svakom slučaju, što nas više, to bolje - brže riješimo pitanja. 
(Inače, za udaranjem drvenom štapigom po glavi uistinu nikad nema potrebe, ako baš vas to personalno ne veseli - demonstratori služe da vam pomognu i ako nešto ne znate, znatno je mudrije sad doći i daviti koga već stignete da vam pomogne, nego daviti s istim pitanjima sljedeće godine.  ) )
|
|
| [Vrh] |
|
klopka
Forumaš(ica)
Pridružen/a: 20. 01. 2011. (10:10:02)
Postovi: (1B)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 19:45 pet, 21. 1. 2011 Naslov: Postano: 19:45 pet, 21. 1. 2011 Naslov: |
    |
|
|
Osjećam duboku potrebu da se ispravim potencijalnim oštećenicima (ako se ne varam, radi se o dvojici muških slušatelja sa sjeverne strane učionice :D) za grešku koju smo sva trojica u nekom trenutku napravili. Naime, [latex]\displaystyle\lim_{x\to \pi/3}\frac{1-2\cos x}{\pi -3x}[/latex] postoji i iznosi [latex]-\displaystyle\frac{\sqrt{3}}{3}[/latex], kao što je kolega br. 2 ispravno zaključio (eventualno nedopuštenim) L'Hôpitalom. Zadatak se lako riješi supstitucijom [latex]t:=x-\pi/3\to 0[/latex]. Nažalost, kalkulator koji smo i ja i on koristili, pretpostavljam, za vrijednosti kosinusa je uzimao stupnjeve, a ne radijane, pa nije davao smislene vrijednosti. :oops:
Stoga se potvrdila kriva teorija kolege br. 1 da limes ne postoji. Sad, ja ne znam je li kolega br. 1 negdje prije u svojem (inače smislenom) računu napravio grešku, ili sam ja napravio grešku u objašnjavanju (eventualno zamijenio [latex]t[/latex] s [latex]1/t[/latex], prije je u tome stvar... :oops:), ali, sve u svemu, došli smo do krivog rezultata koji smo potvrdili grešnim računom na kalkulatoru. :)
Ispričavam se još jednom. Ako itko poznaje kojeg od spomenutih kolega br. 1 i br. 2, neka im kaže da sam idiot. :)
Osjećam duboku potrebu da se ispravim potencijalnim oštećenicima (ako se ne varam, radi se o dvojici muških slušatelja sa sjeverne strane učionice  ) za grešku koju smo sva trojica u nekom trenutku napravili. Naime, ) za grešku koju smo sva trojica u nekom trenutku napravili. Naime, 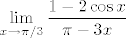 postoji i iznosi postoji i iznosi 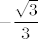 , kao što je kolega br. 2 ispravno zaključio (eventualno nedopuštenim) L'Hôpitalom. Zadatak se lako riješi supstitucijom , kao što je kolega br. 2 ispravno zaključio (eventualno nedopuštenim) L'Hôpitalom. Zadatak se lako riješi supstitucijom 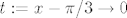 . Nažalost, kalkulator koji smo i ja i on koristili, pretpostavljam, za vrijednosti kosinusa je uzimao stupnjeve, a ne radijane, pa nije davao smislene vrijednosti. . Nažalost, kalkulator koji smo i ja i on koristili, pretpostavljam, za vrijednosti kosinusa je uzimao stupnjeve, a ne radijane, pa nije davao smislene vrijednosti. 
Stoga se potvrdila kriva teorija kolege br. 1 da limes ne postoji. Sad, ja ne znam je li kolega br. 1 negdje prije u svojem (inače smislenom) računu napravio grešku, ili sam ja napravio grešku u objašnjavanju (eventualno zamijenio  s s 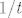 , prije je u tome stvar... , prije je u tome stvar...  ), ali, sve u svemu, došli smo do krivog rezultata koji smo potvrdili grešnim računom na kalkulatoru. ), ali, sve u svemu, došli smo do krivog rezultata koji smo potvrdili grešnim računom na kalkulatoru. 
Ispričavam se još jednom. Ako itko poznaje kojeg od spomenutih kolega br. 1 i br. 2, neka im kaže da sam idiot. 
|
|
| [Vrh] |
|
vuja
Forumaš(ica)


Pridružen/a: 26. 09. 2009. (12:57:07)
Postovi: (2C)16
Spol: 
|
|
| [Vrh] |
|
fejky
Forumaš(ica)
Pridružen/a: 23. 06. 2010. (16:53:45)
Postovi: (3D)16
Spol: 
|
 Postano: 20:40 pet, 21. 1. 2011 Naslov: Postano: 20:40 pet, 21. 1. 2011 Naslov: |
    |
|
|
moze jos jednom? :D
[latex]$\lim_{n\to\,+ \,\infty}\,\,\,(\sqrt{2}-\sqrt[3]{2})\,(\sqrt{2}-\sqrt[5]{2})\,.\,.\,.\,(\sqrt{2}-\sqrt[2n+1]{2})[/latex]
moze jos jednom? 
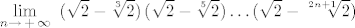
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 20:48 pet, 21. 1. 2011 Naslov: Postano: 20:48 pet, 21. 1. 2011 Naslov: |
    |
|
|
U pitanju je neka želja za sadizmom nad demonstratorima ili? :P
Dakle, za svaki [latex]k\in\mathbb{N}[/latex], [latex]k\geq 2[/latex] vrijedi [latex]0\leq \sqrt{2}-\sqrt[k]{2}\leq \sqrt{2}-1[/latex] - ovo lako provjerimo. Stoga, to specifično vrijedi i za [latex]k=3,5,7,\ldots,2n+1[/latex], što bi reklo, za svaku od ovih zagrada. Tih zagrada tu je [latex]n[/latex], pa znamo da, ako s [latex]P_n[/latex] označimo ovaj produkt u sredini, vrijedi [latex]0=0^n\leq P_n\leq (\sqrt{2}-1)^n[/latex]. Kako je [latex]\sqrt{2}-1[/latex] svakako manji od [latex]1[/latex], [latex](\sqrt{2}-1)^n\to 0[/latex]. Stoga, po teoremu o sendviču, i [latex]P_n\to 0[/latex].
EDIT: Na molbu nadasve pedantne kolegice koja ima i ime i prezime (svako primjerka jednog), ispravljam svoj tipfeler. :oops: :D
U pitanju je neka želja za sadizmom nad demonstratorima ili? 
Dakle, za svaki 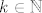 , , 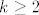 vrijedi vrijedi 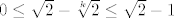 - ovo lako provjerimo. Stoga, to specifično vrijedi i za - ovo lako provjerimo. Stoga, to specifično vrijedi i za 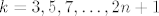 , što bi reklo, za svaku od ovih zagrada. Tih zagrada tu je , što bi reklo, za svaku od ovih zagrada. Tih zagrada tu je  , pa znamo da, ako s , pa znamo da, ako s 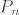 označimo ovaj produkt u sredini, vrijedi označimo ovaj produkt u sredini, vrijedi 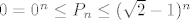 . Kako je . Kako je 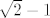 svakako manji od svakako manji od  , , 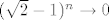 . Stoga, po teoremu o sendviču, i . Stoga, po teoremu o sendviču, i  . .
EDIT: Na molbu nadasve pedantne kolegice koja ima i ime i prezime (svako primjerka jednog), ispravljam svoj tipfeler.  
Zadnja promjena: mornik; 21:41 pet, 21. 1. 2011; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
fejky
Forumaš(ica)
Pridružen/a: 23. 06. 2010. (16:53:45)
Postovi: (3D)16
Spol: 
|
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 20:06 ned, 23. 1. 2011 Naslov: Postano: 20:06 ned, 23. 1. 2011 Naslov: |
    |
|
|
Eventualno da kolegica medonja kaže u čemu je problem (ako se radi o ovom zadatku kojeg sam baš neposredno prije rješavao - s produktom zagrada)... :P Mislim, ideja iza ograničavanja je dosta jasna: vidimo da je [latex]\displaystyle \lim_{n} \sqrt{2}-\sqrt[n]{2}=\sqrt{2}-1[/latex], pa mi zapravo želimo iskoristiti da, kako povećavamo broj zagrada u ovom produktu, množimo s brojevima sličnima [latex]\sqrt{2}-1\sim 0.4[/latex] (ovo je sad, naravno, vrlo neprecizno, ali to je neka generalna ideja). Stoga, u ovom trenutku razmišljamo o tome da je zapravo limes "tu negdje" jednak [latex]\lim_n (\sqrt{2}-1)^n=0[/latex] (kažem, ovo je toliko neprecizno da se dimi, ali ideja je bitna :D).
E, sad, to ćemo probati pokazati teoremom o sendviču: s jedne su strane svi ovi članovi veći od [latex]0[/latex]: [latex]\sqrt{2}-\sqrt[k]{2}>0\Leftrightarrow \sqrt{2}>\sqrt[k]{2}\Leftrightarrow 2^{k/2}>2[/latex], što stoji za sve [latex]k\geq 3[/latex] (a upravo su nam takvi u ovim zagradama). Stoga, i umnožak tih članova je veći od [latex]0[/latex]. S druge strane, svaki od ovih članova je manji od [latex]\sqrt{2}-1[/latex] (primijeti da smo tu mogli pokazati i da je manji od [latex]0.9[/latex], svejedno nam je, ali je ovo dosta prirodno). Naravno, to stoji jer je [latex]\sqrt{2}-1>\sqrt{2}-\sqrt[k]{2}[/latex] ekvivalentno s [latex]\sqrt[k]{2}>1[/latex], što jest. :)
E, sad, imamo [latex]n[/latex] zagrada (prebroji! :)), a svaka je pozitivna i manja od [latex]\sqrt{2}-1[/latex]. Dakle, njihov umnožak je pozitivan i manji od [latex](\sqrt{2}-1)(\sqrt{2}-1)\cdots(\sqrt{2}-1)=(\sqrt{2}-1)^n[/latex].
Dakle, dobili smo da je za svaki [latex]n[/latex] ovaj umnožak između [latex]0[/latex] i [latex](\sqrt{2}-1)^n[/latex]. Kako oba ova niza konvergiraju u nulu, tako i naš traženi niz po teoremu o sendviču konvergira u [latex]0[/latex].
Evo, nadam se da pomaže (i da nisam promašio zadatak). :)
Eventualno da kolegica medonja kaže u čemu je problem (ako se radi o ovom zadatku kojeg sam baš neposredno prije rješavao - s produktom zagrada)...  Mislim, ideja iza ograničavanja je dosta jasna: vidimo da je Mislim, ideja iza ograničavanja je dosta jasna: vidimo da je 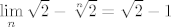 , pa mi zapravo želimo iskoristiti da, kako povećavamo broj zagrada u ovom produktu, množimo s brojevima sličnima , pa mi zapravo želimo iskoristiti da, kako povećavamo broj zagrada u ovom produktu, množimo s brojevima sličnima 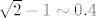 (ovo je sad, naravno, vrlo neprecizno, ali to je neka generalna ideja). Stoga, u ovom trenutku razmišljamo o tome da je zapravo limes "tu negdje" jednak (ovo je sad, naravno, vrlo neprecizno, ali to je neka generalna ideja). Stoga, u ovom trenutku razmišljamo o tome da je zapravo limes "tu negdje" jednak 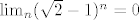 (kažem, ovo je toliko neprecizno da se dimi, ali ideja je bitna (kažem, ovo je toliko neprecizno da se dimi, ali ideja je bitna  ). ).
E, sad, to ćemo probati pokazati teoremom o sendviču: s jedne su strane svi ovi članovi veći od  : : 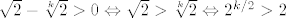 , što stoji za sve , što stoji za sve 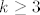 (a upravo su nam takvi u ovim zagradama). Stoga, i umnožak tih članova je veći od (a upravo su nam takvi u ovim zagradama). Stoga, i umnožak tih članova je veći od  . S druge strane, svaki od ovih članova je manji od . S druge strane, svaki od ovih članova je manji od 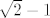 (primijeti da smo tu mogli pokazati i da je manji od (primijeti da smo tu mogli pokazati i da je manji od 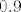 , svejedno nam je, ali je ovo dosta prirodno). Naravno, to stoji jer je , svejedno nam je, ali je ovo dosta prirodno). Naravno, to stoji jer je 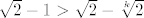 ekvivalentno s ekvivalentno s 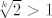 , što jest. , što jest. 
E, sad, imamo  zagrada (prebroji! zagrada (prebroji!  ), a svaka je pozitivna i manja od ), a svaka je pozitivna i manja od 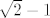 . Dakle, njihov umnožak je pozitivan i manji od . Dakle, njihov umnožak je pozitivan i manji od 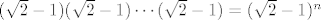 . .
Dakle, dobili smo da je za svaki  ovaj umnožak između ovaj umnožak između  i i 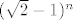 . Kako oba ova niza konvergiraju u nulu, tako i naš traženi niz po teoremu o sendviču konvergira u . Kako oba ova niza konvergiraju u nulu, tako i naš traženi niz po teoremu o sendviču konvergira u  . .
Evo, nadam se da pomaže (i da nisam promašio zadatak). 
|
|
| [Vrh] |
|
|







