|
Iskreno, nikako ne vidim tvoj tok misli, jer ta 2 skupa nisu ni slicna... ma, da ne objasnjavam zasto sad, vidjet ce se iz mog rjesenja zadatka, vrijedi:
[latex]\left\lfloor \sqrt{n} \right\rfloor \leq \sqrt n < \left\lfloor \sqrt{n} \right\rfloor + 1 \implies 0 \leq \sqrt n - \left\lfloor \sqrt{n} \right\rfloor < 1 \qquad (1)[/latex]
Iz ovog slutimo da su nam infimum i supremum 0 i 1. Infimum dobijemo lako, uvrstimo [latex]n = m^2[/latex]. Supremum je nesto zahtjevniji za dobiti. Mi zelimo da nam je razlika izmedju [latex]\sqrt{n}[/latex] i [latex]\left\lfloor \sqrt{n} \right\rfloor[/latex] sto veca, pa cemo promatrati ovakav podskup [latex]S' = \left\{ \sqrt {m^2 - 1} - \left\lfloor \sqrt{m^2 - 1} \right\rfloor : m > 1\right\}[/latex]. Sad, zasto bas tako? Vrijedi:
[latex]m - 1 < \sqrt{m^2 - 1} < m, \quad m > 1[/latex]
pa nam je [latex]\left\lfloor \sqrt{m^2 - 1} \right\rfloor = m - 1[/latex].
S druge strane, [latex]\sqrt{m^2 - 1}[/latex] nam se blizi [latex]m[/latex]-u.
Uzevsi u obzir prethodno, [latex]S' = \left\{ \sqrt{m^2 - 1} - m + 1: m > 1 \right\}[/latex].
Nadalje,
[latex]\displaystyle\lim_{m \to \infty} \left( \sqrt{m^2 - 1} - m + 1 \right) = \displaystyle\lim_{m \to \infty} \displaystyle \frac{(m^2 - 1) - m^2}{m + \sqrt{m^2 - 1}} + 1 = 1[/latex]
Dakle, [latex]1[/latex] je gomilište niza [latex]\sqrt n - \left\lfloor \sqrt n \right\rfloor[/latex], a iz [latex](1)[/latex] slijedi da je najveće gomilište, dakle [latex]\sup S = 1[/latex].
Iskreno, nikako ne vidim tvoj tok misli, jer ta 2 skupa nisu ni slicna... ma, da ne objasnjavam zasto sad, vidjet ce se iz mog rjesenja zadatka, vrijedi:

Iz ovog slutimo da su nam infimum i supremum 0 i 1. Infimum dobijemo lako, uvrstimo 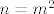 . Supremum je nesto zahtjevniji za dobiti. Mi zelimo da nam je razlika izmedju . Supremum je nesto zahtjevniji za dobiti. Mi zelimo da nam je razlika izmedju  i i 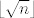 sto veca, pa cemo promatrati ovakav podskup sto veca, pa cemo promatrati ovakav podskup  . Sad, zasto bas tako? Vrijedi: . Sad, zasto bas tako? Vrijedi:

pa nam je 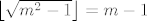 . .
S druge strane,  nam se blizi nam se blizi  -u. -u.
Uzevsi u obzir prethodno,  . .
Nadalje,
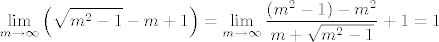
Dakle,  je gomilište niza je gomilište niza  , a iz , a iz 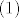 slijedi da je najveće gomilište, dakle slijedi da je najveće gomilište, dakle 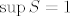 . .
|





