| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
delboy
Forumaš(ica)


Pridružen/a: 02. 11. 2010. (20:33:40)
Postovi: (C)16
Lokacija: Nelson Mandela House,Peckham
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 12:27 uto, 25. 1. 2011 Naslov: Re: ovogodišnji 2 kolokvij Postano: 12:27 uto, 25. 1. 2011 Naslov: Re: ovogodišnji 2 kolokvij |
    |
|
|
Sjeti se raspisa da za svake prirodne brojeve [latex]a[/latex] i [latex]b[/latex] postoje cijeli brojevi [latex]k[/latex] i [latex]l[/latex] takvi da vrijedi [latex]a \cdot k + b \cdot l = M(a,b)[/latex].
S obzirom da se traži najmanji prirodni broj za takav raspis, pitamo se postoji li broj veći ili jednak [latex]1[/latex], a manji od [latex]M(a,b)[/latex] takav da se može raspisati kako je zadano u zadatku. Lako se pokaže da to nije moguće (zbog zajedničkih faktora oba broja s lijeve strane, isti moraju dijeliti i desnu stranu) pa je konačno rješenje [latex]M(a,b)[/latex]. :)
Sjeti se raspisa da za svake prirodne brojeve  i i 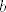 postoje cijeli brojevi postoje cijeli brojevi  i i 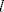 takvi da vrijedi takvi da vrijedi 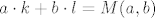 . .
S obzirom da se traži najmanji prirodni broj za takav raspis, pitamo se postoji li broj veći ili jednak  , a manji od , a manji od 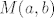 takav da se može raspisati kako je zadano u zadatku. Lako se pokaže da to nije moguće (zbog zajedničkih faktora oba broja s lijeve strane, isti moraju dijeliti i desnu stranu) pa je konačno rješenje takav da se može raspisati kako je zadano u zadatku. Lako se pokaže da to nije moguće (zbog zajedničkih faktora oba broja s lijeve strane, isti moraju dijeliti i desnu stranu) pa je konačno rješenje 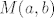 . . 
|
|
| [Vrh] |
|
Macaflyyyyertina_
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (21:06:48)
Postovi: (1C)16
Spol: 
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 16:06 sri, 26. 1. 2011 Naslov: Postano: 16:06 sri, 26. 1. 2011 Naslov: |
    |
|
|
Da, velike su potencije pa je teško dijeliti "ručno". Možda ako uočiš kakvu pravilnost pri dijeljenju, ali opet...
Dakle, znamo da postoje polinomi [latex]q[/latex] i [latex]r[/latex] takvi da vrijedi: [latex]f(x)=g(x) \dot q(x)+r(x), st(r)<st(g)=3 \rightarrow r(x)=ax^2+bx+c, a,b,c \in \mathbb{R}[/latex].
Kada bi [latex]S[/latex] bila nultočka polinoma [latex]g[/latex], tada bi imali: [latex]f(S)=g(S) \dot q(S)+r(S) \Leftrightarrow f(S)=r(S)=aS^2+bS+c[/latex]. Bilo bi korisno pronaći nultočke funkcije [latex]g[/latex] tako da dalje rješavamo zadatak.
No, što ako pri pronalaženju nultočaka tog polinoma naiđemo na višestruku nultočku? Konkretno u ovom zadatku, pronašli smo dvostruku nultočku polinoma [latex]g[/latex] (nazovimo je [latex]t[/latex]), što znači da je [latex]g(t)=0[/latex], ali i [latex]g'(t)=0[/latex].
Sada deriviramo relaciju [latex]f(x)=g(x) \dot q(x)+ax^2+bx+c[/latex] i dobivamo: [latex]f'(x)=g'(x) \dot q(x)+g(x) \dot q'(x)+2ax+b[/latex]. Uvrštavanjem [latex]x=t[/latex] slijedi: [latex]f'(t)=2at+b[/latex]
Konačno, imamo jednostruku nultočku [latex]S[/latex] i dvostruku nultočku [latex]t[/latex] polinoma [latex]g[/latex]. Dobivamo sljedeće tri jednadžbe:
[latex]f(S)=aS^2+bS+c[/latex]
[latex]f(t)=at^2+bt+c[/latex]
[latex]f'(t)=2at+b[/latex]
Vrijednosti [latex]f(S)[/latex], [latex]f(t)[/latex] i [latex]f'(t)[/latex] nije teško izračunati: samo se uvrsti tražena vrijednost i uz to derivira polinom [latex]f[/latex]. Sada se navedeni sustav svodi na sustav triju jednadžbi s trima nepoznanicama ([latex]a[/latex], [latex]b[/latex] i [latex]c[/latex]). Pronađi nepoznanice i imaš rješenje koje si tražio: [latex]r(x)=ax^2+bx+c[/latex], odnosno ostatak pri dijeljenju polinoma! :D
Da, velike su potencije pa je teško dijeliti "ručno". Možda ako uočiš kakvu pravilnost pri dijeljenju, ali opet...
Dakle, znamo da postoje polinomi  i i  takvi da vrijedi: takvi da vrijedi: 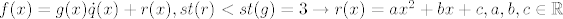 . .
Kada bi  bila nultočka polinoma bila nultočka polinoma  , tada bi imali: , tada bi imali: 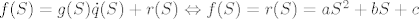 . Bilo bi korisno pronaći nultočke funkcije . Bilo bi korisno pronaći nultočke funkcije  tako da dalje rješavamo zadatak. tako da dalje rješavamo zadatak.
No, što ako pri pronalaženju nultočaka tog polinoma naiđemo na višestruku nultočku? Konkretno u ovom zadatku, pronašli smo dvostruku nultočku polinoma  (nazovimo je (nazovimo je  ), što znači da je ), što znači da je 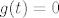 , ali i , ali i 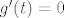 . .
Sada deriviramo relaciju 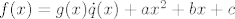 i dobivamo: i dobivamo: 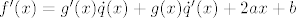 . Uvrštavanjem . Uvrštavanjem 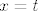 slijedi: slijedi: 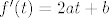
Konačno, imamo jednostruku nultočku  i dvostruku nultočku i dvostruku nultočku  polinoma polinoma  . Dobivamo sljedeće tri jednadžbe: . Dobivamo sljedeće tri jednadžbe:
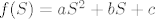
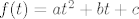
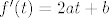
Vrijednosti 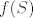 , , 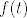 i i 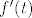 nije teško izračunati: samo se uvrsti tražena vrijednost i uz to derivira polinom nije teško izračunati: samo se uvrsti tražena vrijednost i uz to derivira polinom  . Sada se navedeni sustav svodi na sustav triju jednadžbi s trima nepoznanicama ( . Sada se navedeni sustav svodi na sustav triju jednadžbi s trima nepoznanicama ( , , 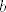 i i  ). Pronađi nepoznanice i imaš rješenje koje si tražio: ). Pronađi nepoznanice i imaš rješenje koje si tražio: 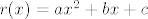 , odnosno ostatak pri dijeljenju polinoma! , odnosno ostatak pri dijeljenju polinoma! 
|
|
| [Vrh] |
|
Macaflyyyyertina_
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (21:06:48)
Postovi: (1C)16
Spol: 
|
|
| [Vrh] |
|
654321
Forumaš(ica)

Pridružen/a: 18. 01. 2011. (18:30:01)
Postovi: (D)16
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 20:05 sri, 26. 1. 2011 Naslov: Postano: 20:05 sri, 26. 1. 2011 Naslov: |
    |
|
|
[quote="654321"]nije mi jasno samo kako izracunam f(s), f(t) i f'(t)... Koju traženu vrijednost moram uvrstit i koji polinom f deriviram??[/quote]
U mom primjeru, [latex]S[/latex] je jednostruka točka, a [latex]t[/latex] dvostruka nultočka polinoma [latex]g[/latex].
Evo, primjer za prvu grupu: [latex]g(x)=x^3-7x^2+15x-9=(x-1)(x-3)^2[/latex], pa je jednostruka nultočka [latex]S=1[/latex], a dvostruka [latex]t=3[/latex].
A polinom koji moraš derivirati je upravo sam [latex]f[/latex] ("onaj s visokim stupnjevima"). Njega deriviramo zato što tražimo koliko je [latex]f'(t)[/latex], a znamo [latex]f(x)[/latex] i znamo [latex]t[/latex]. Pogledaj sustav jednadžbi raspisan u mom prethodnom postu. :)
| 654321 (napisa): | | nije mi jasno samo kako izracunam f(s), f(t) i f'(t)... Koju traženu vrijednost moram uvrstit i koji polinom f deriviram?? |
U mom primjeru,  je jednostruka točka, a je jednostruka točka, a  dvostruka nultočka polinoma dvostruka nultočka polinoma  . .
Evo, primjer za prvu grupu: 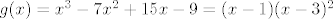 , pa je jednostruka nultočka , pa je jednostruka nultočka 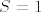 , a dvostruka , a dvostruka  . .
A polinom koji moraš derivirati je upravo sam  ("onaj s visokim stupnjevima"). Njega deriviramo zato što tražimo koliko je ("onaj s visokim stupnjevima"). Njega deriviramo zato što tražimo koliko je 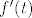 , a znamo , a znamo 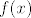 i znamo i znamo  . Pogledaj sustav jednadžbi raspisan u mom prethodnom postu. . Pogledaj sustav jednadžbi raspisan u mom prethodnom postu. 
|
|
| [Vrh] |
|
654321
Forumaš(ica)

Pridružen/a: 18. 01. 2011. (18:30:01)
Postovi: (D)16
|
|
| [Vrh] |
|
Macaflyyyyertina_
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (21:06:48)
Postovi: (1C)16
Spol: 
|
|
| [Vrh] |
|
|







