| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
jejo
Forumaš(ica)

Pridružen/a: 28. 11. 2006. (19:25:36)
Postovi: (102)16
Spol: 
|
|
| [Vrh] |
|
tidus
Forumaš(ica)


Pridružen/a: 16. 02. 2009. (12:47:59)
Postovi: (A5)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 10:17 sri, 2. 2. 2011 Naslov: Postano: 10:17 sri, 2. 2. 2011 Naslov: |
    |
|
|
[quote="tidus"]Može li mi netko rješit 5. zadatak drugog kolokvija 2010/2011 (kojeg smo upravo pisali)?
kolokvij:
http://web.math.hr/nastava/vekt/files/2010-11/kol2_10_11.pdf[/quote]
Znamo da je operator [latex]P[/latex] ortogonalni projektor ako i samo ako je [latex]P=P^*[/latex] i [latex]P=P^2[/latex], zadano nam je da [latex]P[/latex] je hermitski, dakle, dovoljno je pokazati da je [latex]P=P^2 \Longleftrightarrow P=P^{11}=P^{15}=P^{36}[/latex].
Indukcijom direktno slijedi da ako je [latex]P=P^2[/latex] da je onda [latex]P=P^n\ \forall n \in \mathbb{N}[/latex]. Obratno, vrijedi [latex]P^2=P \cdot P = P^{11} \cdot P^{15} = P^{26} = P \cdot P^{25} = P^{11} \cdot P^{25} = P^{36} = P[/latex].
U drugoj grupi je ista šema... :-)
[quote="Anonymous"]http://web.math.hr/nastava/vekt/files/2009-10/popravak_2kol_0910.pdf
jel bi mogo netko 6. i 7. (prva grupa) rjesit? hvala[/quote]
6. Kako je operator normalan znamo da se on dijagonalizira u nekoj ortonormiranoj bazi, njegove potencijalne svojstvene vrjednosti su -1, 0 i 1, dnosno, sve su realne, pa je onda njegov prikaz u toj bazi hermitksa matrica, dakle, operator je hermitski.
7. Kako je P pozitivan, znači da su mu u spektru samo pozitivni realni brojevi. Operator je unitaran ako i samo ako su mu sve svojstvene vrijednosti norme 1. Dakle, mora biti [latex]|x^2+2x|=1[/latex], kako je [latex]x>0[/latex] vidimo da je jedina mogućnost [latex]x=\sqrt{2}-1[/latex].
Znamo da je operator  ortogonalni projektor ako i samo ako je ortogonalni projektor ako i samo ako je 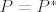 i i 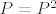 , zadano nam je da , zadano nam je da  je hermitski, dakle, dovoljno je pokazati da je je hermitski, dakle, dovoljno je pokazati da je 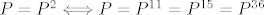 . .
Indukcijom direktno slijedi da ako je 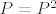 da je onda da je onda 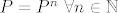 . Obratno, vrijedi . Obratno, vrijedi 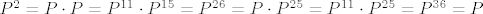 . .
U drugoj grupi je ista šema... 
| Anonymous (napisa): | http://web.math.hr/nastava/vekt/files/2009-10/popravak_2kol_0910.pdf
jel bi mogo netko 6. i 7. (prva grupa) rjesit? hvala |
6. Kako je operator normalan znamo da se on dijagonalizira u nekoj ortonormiranoj bazi, njegove potencijalne svojstvene vrjednosti su -1, 0 i 1, dnosno, sve su realne, pa je onda njegov prikaz u toj bazi hermitksa matrica, dakle, operator je hermitski.
7. Kako je P pozitivan, znači da su mu u spektru samo pozitivni realni brojevi. Operator je unitaran ako i samo ako su mu sve svojstvene vrijednosti norme 1. Dakle, mora biti 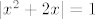 , kako je , kako je 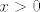 vidimo da je jedina mogućnost vidimo da je jedina mogućnost 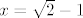 . .
|
|
| [Vrh] |
|
tidus
Forumaš(ica)


Pridružen/a: 16. 02. 2009. (12:47:59)
Postovi: (A5)16
Spol: 
|
 Postano: 11:00 sri, 2. 2. 2011 Naslov: Postano: 11:00 sri, 2. 2. 2011 Naslov: |
    |
|
|
[quote="JANKRI"][quote="Anonymous"]http://web.math.hr/nastava/vekt/files/2009-10/popravak_2kol_0910.pdf
jel bi mogo netko 6. i 7. (prva grupa) rjesit? hvala[/quote]
6. Kako je operator normalan znamo da se on dijagonalizira u nekoj ortonormiranoj bazi, njegove potencijalne svojstvene vrjednosti su -1, 0 i 1, dnosno, sve su realne, pa je onda njegov prikaz u toj bazi hermitksa matrica, dakle, operator je hermitski.
[/quote]
Zašto je uopće važno da se može dijagonalizirat, tj. da je normalan? Ako imam da su svojstvene vrijednosti realne, zar nebi iz toga već mogli zaključit da je operator hermitski?
| JANKRI (napisa): | | Anonymous (napisa): | http://web.math.hr/nastava/vekt/files/2009-10/popravak_2kol_0910.pdf
jel bi mogo netko 6. i 7. (prva grupa) rjesit? hvala |
6. Kako je operator normalan znamo da se on dijagonalizira u nekoj ortonormiranoj bazi, njegove potencijalne svojstvene vrjednosti su -1, 0 i 1, dnosno, sve su realne, pa je onda njegov prikaz u toj bazi hermitksa matrica, dakle, operator je hermitski.
|
Zašto je uopće važno da se može dijagonalizirat, tj. da je normalan? Ako imam da su svojstvene vrijednosti realne, zar nebi iz toga već mogli zaključit da je operator hermitski?
|
|
| [Vrh] |
|
Gost
|
 Postano: 11:09 sri, 2. 2. 2011 Naslov: Postano: 11:09 sri, 2. 2. 2011 Naslov: |
    |
|
|
[quote="tidus"][quote="JANKRI"][quote="Anonymous"]http://web.math.hr/nastava/vekt/files/2009-10/popravak_2kol_0910.pdf
jel bi mogo netko 6. i 7. (prva grupa) rjesit? hvala[/quote]
6. Kako je operator normalan znamo da se on dijagonalizira u nekoj ortonormiranoj bazi, njegove potencijalne svojstvene vrjednosti su -1, 0 i 1, dnosno, sve su realne, pa je onda njegov prikaz u toj bazi hermitksa matrica, dakle, operator je hermitski.
[/quote]
Zašto je uopće važno da se može dijagonalizirat, tj. da je normalan? Ako imam da su svojstvene vrijednosti realne, zar nebi iz toga već mogli zaključit da je operator hermitski?[/quote]
što nije po definiciji: A normalan, tada A hermitski akko svj, vrijednosti realne?
| tidus (napisa): | | JANKRI (napisa): | | Anonymous (napisa): | http://web.math.hr/nastava/vekt/files/2009-10/popravak_2kol_0910.pdf
jel bi mogo netko 6. i 7. (prva grupa) rjesit? hvala |
6. Kako je operator normalan znamo da se on dijagonalizira u nekoj ortonormiranoj bazi, njegove potencijalne svojstvene vrjednosti su -1, 0 i 1, dnosno, sve su realne, pa je onda njegov prikaz u toj bazi hermitksa matrica, dakle, operator je hermitski.
|
Zašto je uopće važno da se može dijagonalizirat, tj. da je normalan? Ako imam da su svojstvene vrijednosti realne, zar nebi iz toga već mogli zaključit da je operator hermitski? |
što nije po definiciji: A normalan, tada A hermitski akko svj, vrijednosti realne?
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
:)
Forumaš(ica)
Pridružen/a: 25. 04. 2009. (16:17:14)
Postovi: (66)16
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
|








