| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
LB
Forumaš(ica)
Pridružen/a: 25. 11. 2008. (15:04:31)
Postovi: (20)16
Spol: 
Lokacija: U zoni Sumraka
|
 Postano: 17:30 sri, 27. 1. 2010 Naslov: Postano: 17:30 sri, 27. 1. 2010 Naslov: |
    |
|
|
Evo ako nekome pomaže, danas sam bila na usmenom, profesor nas je pitao troje odjednom, svakom postavlja po jedno pitanje u dva kruga. U prvom krugu je kao pitanje bio postavljen zadatak sa separiranim dif. jednadžbama, a u drugom krugu je bila dif. jednadžba trećeg reda. Dakle, profesor traži da razumijete što se u zadatku traži, da li postoji jedinstveno rješenje, na kojem intervalu itd. Sretno svima! :)
Evo ako nekome pomaže, danas sam bila na usmenom, profesor nas je pitao troje odjednom, svakom postavlja po jedno pitanje u dva kruga. U prvom krugu je kao pitanje bio postavljen zadatak sa separiranim dif. jednadžbama, a u drugom krugu je bila dif. jednadžba trećeg reda. Dakle, profesor traži da razumijete što se u zadatku traži, da li postoji jedinstveno rješenje, na kojem intervalu itd. Sretno svima! 
_________________
Vrijeme je sjajan učitelj, ali nažalost ubija sve svoje učenike...
-Louis Hector Berlioz-
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
psujetic
Forumaš(ica)
Pridružen/a: 27. 04. 2007. (21:11:30)
Postovi: (13)16
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 18:23 čet, 3. 2. 2011 Naslov: Postano: 18:23 čet, 3. 2. 2011 Naslov: |
    |
|
|
kolko sam skužio od kolega, nikog nije ispitivao neproširivo rješenje, a eksponencijalna funkcija amtrice bla bla kak li se već zove ti je sam dokaz onog teorema kak izgledaju funkcije fundamentalne matrice
a zašt su zvjezdice, e to stvarno ne bih znao
[size=9][color=#999999]Added after 7 minutes:[/color][/size]
ovo se odnosi na usmeni kod prof Vrdoljaka, nisam ni čitao ime teme
kolko sam skužio od kolega, nikog nije ispitivao neproširivo rješenje, a eksponencijalna funkcija amtrice bla bla kak li se već zove ti je sam dokaz onog teorema kak izgledaju funkcije fundamentalne matrice
a zašt su zvjezdice, e to stvarno ne bih znao
Added after 7 minutes:
ovo se odnosi na usmeni kod prof Vrdoljaka, nisam ni čitao ime teme
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
ankovacic
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (19:28:17)
Postovi: (5C)16
Spol: 
|
 Postano: 10:27 pet, 27. 1. 2012 Naslov: Postano: 10:27 pet, 27. 1. 2012 Naslov: |
    |
|
|
kolege, ne trebate se ničeg bojat, profesor je krajnje ugodan na usmenom, prvo počne o tome ko bolje briše ploču (dečki ili cure) pa onda kak je lijepo vrijeme vani za izić i prošetat se i onda krene..
Pitanja koja je meni postavio:
[latex]u'=u(1-u^2)[/latex]
Što možeš reći o jedinstvenosti, koje teoreme možeš upotrijebit, kakav je ovo oblik jdbe (autonomna), koja su ravnotežna stanja jesu li stabilna, nacrtajte ih, nacrtajte x, u ravninu i prikaz rješenja za [latex]u(0)=u_0[/latex] gdje je [latex]u(0)=u_0 [/latex] broj između 0 i jedan, zatim veći od jedan kako onda znamo (za veće od jedan da riješenje ne "krivuda" oko ravnotežnog stanja nego se ponaša monotono (padajuće se približava prema 1)), jeli sustav stabilan, onda me krenuo ispitivat s matricama, zadao mi je matricu oblika
[latex]\[ \left( \begin{array}{ccc}
-1 & 1\\
0 & -1 \\
\end{array} \right)\][/latex]
Što mogu reći o sustavu
[latex]U'=AU[/latex]
Dakle to je autonoman sustav, svojstvene vrijednosti, jeli stabilan...
Onda me je pitao za ovaj sustav:
[latex]\[ \left( \begin{array}{ccc}
0 & 1\\
0 & 0 \\
\end{array} \right)\][/latex]
Što kaže teorem o ekvivalenciji o tom sustavu (morao sam mu napisati linearnu jdbu višeg reda koja po teoremu o ekvivalenciji ima zadanu ovu matricu, dakle [latex]u''=0[/latex]). I rekao mi je da izračunam [latex]e^A[/latex] te me pitao kako definiramo evolucionu matricu i to je to... jedan od najboljih usmenih što sam imao...
Dakle, dobio sam 4 a imao sam sve skupa s kolokvija ravno 125 bodova tako da možete povisiti ocjenu za 2 (a možda i više)...
kolege, ne trebate se ničeg bojat, profesor je krajnje ugodan na usmenom, prvo počne o tome ko bolje briše ploču (dečki ili cure) pa onda kak je lijepo vrijeme vani za izić i prošetat se i onda krene..
Pitanja koja je meni postavio:
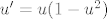
Što možeš reći o jedinstvenosti, koje teoreme možeš upotrijebit, kakav je ovo oblik jdbe (autonomna), koja su ravnotežna stanja jesu li stabilna, nacrtajte ih, nacrtajte x, u ravninu i prikaz rješenja za 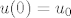 gdje je gdje je 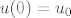 broj između 0 i jedan, zatim veći od jedan kako onda znamo (za veće od jedan da riješenje ne "krivuda" oko ravnotežnog stanja nego se ponaša monotono (padajuće se približava prema 1)), jeli sustav stabilan, onda me krenuo ispitivat s matricama, zadao mi je matricu oblika broj između 0 i jedan, zatim veći od jedan kako onda znamo (za veće od jedan da riješenje ne "krivuda" oko ravnotežnog stanja nego se ponaša monotono (padajuće se približava prema 1)), jeli sustav stabilan, onda me krenuo ispitivat s matricama, zadao mi je matricu oblika
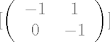
Što mogu reći o sustavu
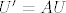
Dakle to je autonoman sustav, svojstvene vrijednosti, jeli stabilan...
Onda me je pitao za ovaj sustav:

Što kaže teorem o ekvivalenciji o tom sustavu (morao sam mu napisati linearnu jdbu višeg reda koja po teoremu o ekvivalenciji ima zadanu ovu matricu, dakle 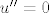 ). I rekao mi je da izračunam ). I rekao mi je da izračunam 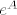 te me pitao kako definiramo evolucionu matricu i to je to... jedan od najboljih usmenih što sam imao... te me pitao kako definiramo evolucionu matricu i to je to... jedan od najboljih usmenih što sam imao...
Dakle, dobio sam 4 a imao sam sve skupa s kolokvija ravno 125 bodova tako da možete povisiti ocjenu za 2 (a možda i više)...
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
kobila krsto
Forumaš(ica)
Pridružen/a: 02. 07. 2009. (16:55:08)
Postovi: (6A)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
minnie m.
Forumaš(ica)

Pridružen/a: 06. 10. 2011. (20:34:28)
Postovi: (16)16
|
|
| [Vrh] |
|
holidayRainbowLights
Forumaš(ica)


Pridružen/a: 28. 03. 2012. (23:58:54)
Postovi: (11)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|











