|
Neka je [latex](x_n)[/latex] proizvoljan niz realnih brojeva većih od 1 koji divergira u pozitivnu beskonačnost. Definirajmo niz prirodnih brojeva [latex](a_n)[/latex] tako da je [latex]a_n \leq x_n < a_n + 1[/latex], za svaki [latex]n \in \mathbb{N}[/latex]. Očito i niz [latex](a_n)[/latex] divergira u pozitivnu beskonačnost. Tada je
[latex]$\begin{align*}
\frac{\left( 1 + \frac{1}{a_n + 1} \right)^{a_n + 1}}{1 + \frac{1}{a_n + 1}}
= \left( 1 + \frac{1}{a_n + 1} \right)^{a_n}
< & \left( 1 + \frac{1}{x_n} \right)^{a_n} \leq \\
\leq & \left( 1 + \frac{1}{x_n} \right)^{x_n} < \\
< & \left( 1 + \frac{1}{x_n} \right)^{a_n + 1}
\leq \left( 1 + \frac{1}{a_n} \right)^{a_n + 1}
= \left( 1 + \frac{1}{a_n} \right) \left( 1 + \frac{1}{a_n} \right)^{a_n}
\end{align*}$[/latex]
Po teoremu o sendviču slijedi tvrdnja.
Par stvari fali, više-manje namjerno, npr. Arhimedov aksiom kod definicije niza [latex](a_n)[/latex], dokaz da [latex]a_n \to +\infty[/latex] (može preko teorema o sendviču), referiranje na rastuće funkcije za dokaz nejednakosti u posljednjem koraku.
Neka je 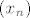 proizvoljan niz realnih brojeva većih od 1 koji divergira u pozitivnu beskonačnost. Definirajmo niz prirodnih brojeva proizvoljan niz realnih brojeva većih od 1 koji divergira u pozitivnu beskonačnost. Definirajmo niz prirodnih brojeva 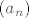 tako da je tako da je 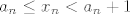 , za svaki , za svaki  . Očito i niz . Očito i niz 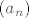 divergira u pozitivnu beskonačnost. Tada je divergira u pozitivnu beskonačnost. Tada je
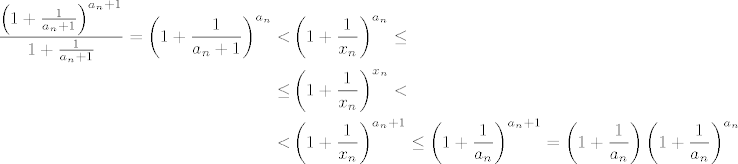
Po teoremu o sendviču slijedi tvrdnja.
Par stvari fali, više-manje namjerno, npr. Arhimedov aksiom kod definicije niza 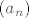 , dokaz da , dokaz da 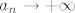 (može preko teorema o sendviču), referiranje na rastuće funkcije za dokaz nejednakosti u posljednjem koraku. (može preko teorema o sendviču), referiranje na rastuće funkcije za dokaz nejednakosti u posljednjem koraku.
|






