| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 10:23 pon, 14. 3. 2011 Naslov: zadaci Postano: 10:23 pon, 14. 3. 2011 Naslov: zadaci |
    |
|
|
muče me 3. i 4. zadatak u http://web.math.hr/nastava/alg/zadace/zadaca1.pdf
u 3.zadatku neznam izračunati inverzni element..((u,v,w) sam uzela za inverzni,pa računam kolko mi je u,v i w)dobim
a1*u=1
a2*u+v=0
a3*u+w=0 za desni inverz
u*a1=1
va1+a2=0
wa1+a3=0 za lijevi
probala sam dosta toga izraziti,pa uvrstiti u formule,ali mi uvijek ispadne 0=0 :(
u 4.zadatku je problem neutralni element.
dobijem x°g°e=e°g°x=x, pa slijedi da je g°e=e°g, i tu sam zapela. Znači li to da je g ili e neutralni element u G, pp da je to g(neznam argumentirati,tak mi se čini :?: ), pa je g°e=e°g=e, iz čega slijedi da je e neutralni element za operaciju *??
I 9.zadatak,njega neznam ni početi :?
muče me 3. i 4. zadatak u http://web.math.hr/nastava/alg/zadace/zadaca1.pdf
u 3.zadatku neznam izračunati inverzni element..((u,v,w) sam uzela za inverzni,pa računam kolko mi je u,v i w)dobim
a1*u=1
a2*u+v=0
a3*u+w=0 za desni inverz
u*a1=1
va1+a2=0
wa1+a3=0 za lijevi
probala sam dosta toga izraziti,pa uvrstiti u formule,ali mi uvijek ispadne 0=0 
u 4.zadatku je problem neutralni element.
dobijem x°g°e=e°g°x=x, pa slijedi da je g°e=e°g, i tu sam zapela. Znači li to da je g ili e neutralni element u G, pp da je to g(neznam argumentirati,tak mi se čini  ), pa je g°e=e°g=e, iz čega slijedi da je e neutralni element za operaciju *?? ), pa je g°e=e°g=e, iz čega slijedi da je e neutralni element za operaciju *??
I 9.zadatak,njega neznam ni početi 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 14:12 pon, 14. 3. 2011 Naslov: Postano: 14:12 pon, 14. 3. 2011 Naslov: |
    |
|
|
Pretpostavljam da u 3. dobivaš 0=0 jer rješavaš nekakav sustav ili što već. Trebaš izraziti u, v i w te provjeriti da je [latex]u\in\mathbb{Q}^*[/latex] (a je, jer [latex]u=a_1^{-1}[/latex], a budući je Q* multiplikativna grupa, tada postoji [latex]a_1^{-1}[/latex]). Slično sa v i w, treba se provjeriti da su u aditivnoj grupi Q, samo se tu možda treba napomenuti da bez obzira što je [latex]a_1^{-1}[/latex] iz Q* da će svejedno on biti i u aditivnoj grupi i da će [latex]a_2a_1^{-1}[/latex] biti u aditivnoj grupi itd.
U 4. slično. Označi sa u inverz u (G,*). Tada je x*u=x akko x°g°u=x. Sada jer je (G,°) grupa možeš koristiti asocijativnost i činjenicu da u (G,°) element g ima inverz. Iz toga možeš izraziti koliki je u. Nakon što izračunaš koliki je u, pogledaj direktnim uvrštavanjem da li je on i lijevi neutral u (G,*)
U 9. prvo pretpostavimo da postoji rješenje od [latex]x^2ax=a^{-1}[/latex] i označimo to rješenje sa [latex]x_1[/latex]. Tada je
[spoiler][latex]ax_1^2ax_1=e\Rightarrow (ax_1)x_1(ax_1)=e \Rightarrow x_1(ax_1)=(ax_1)^{-1}[/latex]
Iz toga dalje slijedi
[latex]x_1(ax_1)(ax_1)=e \Rightarrow ax_1(ax_1)(ax_1)=a \Rightarrow (ax_1)^3=a[/latex]
pa uzmemo [latex]b=ax_1[/latex].[/spoiler]
Obratno se može riješiti pogađanjem ili uvrštavanjem a=b^3 u jednadžbu.
Pretpostavljam da u 3. dobivaš 0=0 jer rješavaš nekakav sustav ili što već. Trebaš izraziti u, v i w te provjeriti da je 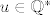 (a je, jer (a je, jer  , a budući je Q* multiplikativna grupa, tada postoji , a budući je Q* multiplikativna grupa, tada postoji 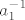 ). Slično sa v i w, treba se provjeriti da su u aditivnoj grupi Q, samo se tu možda treba napomenuti da bez obzira što je ). Slično sa v i w, treba se provjeriti da su u aditivnoj grupi Q, samo se tu možda treba napomenuti da bez obzira što je 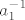 iz Q* da će svejedno on biti i u aditivnoj grupi i da će iz Q* da će svejedno on biti i u aditivnoj grupi i da će  biti u aditivnoj grupi itd. biti u aditivnoj grupi itd.
U 4. slično. Označi sa u inverz u (G,*). Tada je x*u=x akko x°g°u=x. Sada jer je (G,°) grupa možeš koristiti asocijativnost i činjenicu da u (G,°) element g ima inverz. Iz toga možeš izraziti koliki je u. Nakon što izračunaš koliki je u, pogledaj direktnim uvrštavanjem da li je on i lijevi neutral u (G,*)
U 9. prvo pretpostavimo da postoji rješenje od 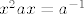 i označimo to rješenje sa i označimo to rješenje sa 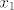 . Tada je . Tada je
| Spoiler [hidden; click to show]: | 
Iz toga dalje slijedi
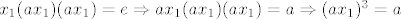
pa uzmemo 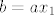 . |
Obratno se može riješiti pogađanjem ili uvrštavanjem a=b^3 u jednadžbu.
_________________
The Dude Abides
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
there is no spoon
Forumaš(ica)

Pridružen/a: 11. 04. 2008. (11:12:06)
Postovi: (36)16
|
|
| [Vrh] |
|
|





