| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
moni_poni
Forumaš(ica)

Pridružen/a: 25. 01. 2010. (19:48:19)
Postovi: (49)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 19:57 sri, 23. 3. 2011 Naslov: Postano: 19:57 sri, 23. 3. 2011 Naslov: |
    |
|
|
Za početak hintovi, jer ne mogu dokučiti do kud si izgurala pojedini zadatak, pa reci ako treba još. :)
1.54 Trebaš naći sve normale funkcije [latex]\displaystyle f(x) = \frac{a^2}{x}[/latex] koje prolaze kroz ishodište.
1.55 Odredi presjeke s koordinatnim osima, nađi tangente u njima i pogledaj kakve koeficijente nagiba si dobila (tj. derivacije u tim točkama).
1.56 Implicitno deriviraj da dobiš nagib tangente u točki [latex](p, q)[/latex], pa to ubaci u izraz za tangentu. Izbjegavaj korijene.
1.57 Nađi sve točke u kojima je derivacija 1.
1.58 Nađi sve točke u kojima je derivacija 0.
1.59 Odredi sjecišta tih krivulja, pa derivacije u njima (za to je najbolje implicitno derivirati).
1.60 Gdje ta parabola siječe os apscisa? Odredi derivacije u tim točkama, pa kuteve.
Za početak hintovi, jer ne mogu dokučiti do kud si izgurala pojedini zadatak, pa reci ako treba još. 
1.54 Trebaš naći sve normale funkcije 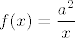 koje prolaze kroz ishodište. koje prolaze kroz ishodište.
1.55 Odredi presjeke s koordinatnim osima, nađi tangente u njima i pogledaj kakve koeficijente nagiba si dobila (tj. derivacije u tim točkama).
1.56 Implicitno deriviraj da dobiš nagib tangente u točki 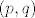 , pa to ubaci u izraz za tangentu. Izbjegavaj korijene. , pa to ubaci u izraz za tangentu. Izbjegavaj korijene.
1.57 Nađi sve točke u kojima je derivacija 1.
1.58 Nađi sve točke u kojima je derivacija 0.
1.59 Odredi sjecišta tih krivulja, pa derivacije u njima (za to je najbolje implicitno derivirati).
1.60 Gdje ta parabola siječe os apscisa? Odredi derivacije u tim točkama, pa kuteve.
|
|
| [Vrh] |
|
moni_poni
Forumaš(ica)

Pridružen/a: 25. 01. 2010. (19:48:19)
Postovi: (49)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 12:21 sub, 26. 3. 2011 Naslov: Postano: 12:21 sub, 26. 3. 2011 Naslov: |
    |
|
|
1.64. je, čini mi se (nisam išao gledati je li to taj zadatak :D), ukratko opisan [url=http://degiorgi.math.hr/forum/viewtopic.php?t=16412&start=20]tu[/url], a 1.63. će ići malo teže, kao što sam i tamo rekao, makar je Ilja dao neke hintove [url=http://degiorgi.math.hr/forum/viewtopic.php?p=134402&highlight=#134402]tu[/url].
1.64. je, čini mi se (nisam išao gledati je li to taj zadatak  ), ukratko opisan tu, a 1.63. će ići malo teže, kao što sam i tamo rekao, makar je Ilja dao neke hintove tu. ), ukratko opisan tu, a 1.63. će ići malo teže, kao što sam i tamo rekao, makar je Ilja dao neke hintove tu.
|
|
| [Vrh] |
|
Joker
Forumaš(ica)

Pridružen/a: 19. 09. 2010. (10:19:16)
Postovi: (8C)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 20:24 čet, 31. 3. 2011 Naslov: Postano: 20:24 čet, 31. 3. 2011 Naslov: |
    |
|
|
Evo, samo na brzinu: u vezi trećeg zadatka, primijeti da je [latex]0\leq|f(x)|=|\ln x\cdot\cos(\frac{1}{x-1})\leq|\ln x|[/latex], a za [latex]x\to 1[/latex], [latex]\ln x\to 0[/latex]. Stoga, traženi limes za [latex]x\to 1[/latex] je [latex]0[/latex]. Sad, dakle, dodefiniramo [latex]f(1)=0[/latex]. Takva funkcija nije neprekidno derivabilna. Dapače, ona nije ni derivabilna u [latex]1[/latex]. Pogledajmo što je [latex]\displaystyle\frac{f(x)-f(1)}{x-1}[/latex]. To je [latex]\displaystyle\frac{\ln x}{x-1}\cos(\frac{1}{x-1})[/latex]. Budući da za [latex]x\to 1[/latex] vrijedi [latex]\frac{\ln x}{x-1}\to 1[/latex], a [latex]\cos(\frac{1}{x-1})[/latex] nema limes za [latex]x\to 1[/latex] (Kad kosinus "ide u beskonačno", i dalje postiže i jedinice i [latex]-1[/latex], tako da nikako ne konvergira. Ovo se, dakako, može i formalnije napisati. :)), ništa od toga. :D
Što se četvrtog tiče, prvo ćemo odrediti koliki su [latex]x[/latex] i [latex]y[/latex]. Iz prve jednadžbe imamo [latex]y=\frac{2}{\sqrt{x}}[/latex], a uvrštavanjem u drugu dobivamo [latex]x^{a-1/2}=1[/latex], tj. [latex]x=1[/latex]. Dakle, radi se o točki [latex](1,2)[/latex]. Sad pogledajmo koji je koeficijent smjera tangenata ove dvije kružnice u tim točkama: za prvu imamo, ako sam ja to sad točno na brzinu izračunao, [latex]y'=\frac{-1}{x^{-3/2}}[/latex], tj. [latex]y'=-1[/latex] u našoj točki. Za drugu imamo valjda [latex]y'=\frac{-2a}{x^{a+1}}[/latex], odnosno [latex]y'=-2a[/latex] u jedinici. (Ponovno, ako sam ja to sve sad dobro izračunao.) Dakle, sad želiš da kut između ove dvije tangente bude [latex]30^\circ[/latex]. E, sad si nacrtaj to na papiru ili što već: dobivaš da druga krivulja mora imati kut [latex]-15^\circ[/latex] ili [latex]-75^\circ[/latex] obzirom na [latex]x[/latex] os. No, onda mora dakle biti [latex]-2a=\tan(-15^\circ)[/latex] ili [latex]-2a=\tan(-75^\circ)[/latex]. Dakle, [latex]a\in\{\tan(15^\circ)/2, \tan(75^\circ)/2[/latex]. Naglašavam, račun nisam provjeravao, tako da je sasvim moguće kriv, ali to bi bila ideja. Rezultat se, čak i ako je točan, sigurno može zapisati i ljepše. :)
Nadam se da je bilo od pomoći. :)
EDIT: Joker, hvala na ispravki. :oops:
Evo, samo na brzinu: u vezi trećeg zadatka, primijeti da je 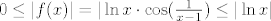 , a za , a za 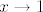 , , 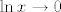 . Stoga, traženi limes za . Stoga, traženi limes za 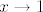 je je  . Sad, dakle, dodefiniramo . Sad, dakle, dodefiniramo 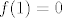 . Takva funkcija nije neprekidno derivabilna. Dapače, ona nije ni derivabilna u . Takva funkcija nije neprekidno derivabilna. Dapače, ona nije ni derivabilna u  . Pogledajmo što je . Pogledajmo što je 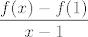 . To je . To je 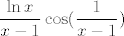 . Budući da za . Budući da za 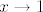 vrijedi vrijedi 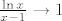 , a , a 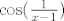 nema limes za nema limes za 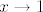 (Kad kosinus "ide u beskonačno", i dalje postiže i jedinice i (Kad kosinus "ide u beskonačno", i dalje postiže i jedinice i  , tako da nikako ne konvergira. Ovo se, dakako, može i formalnije napisati. , tako da nikako ne konvergira. Ovo se, dakako, može i formalnije napisati.  ), ništa od toga. ), ništa od toga. 
Što se četvrtog tiče, prvo ćemo odrediti koliki su  i i  . Iz prve jednadžbe imamo . Iz prve jednadžbe imamo 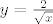 , a uvrštavanjem u drugu dobivamo , a uvrštavanjem u drugu dobivamo 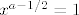 , tj. , tj.  . Dakle, radi se o točki . Dakle, radi se o točki 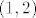 . Sad pogledajmo koji je koeficijent smjera tangenata ove dvije kružnice u tim točkama: za prvu imamo, ako sam ja to sad točno na brzinu izračunao, . Sad pogledajmo koji je koeficijent smjera tangenata ove dvije kružnice u tim točkama: za prvu imamo, ako sam ja to sad točno na brzinu izračunao, 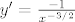 , tj. , tj.  u našoj točki. Za drugu imamo valjda u našoj točki. Za drugu imamo valjda 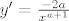 , odnosno , odnosno 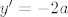 u jedinici. (Ponovno, ako sam ja to sve sad dobro izračunao.) Dakle, sad želiš da kut između ove dvije tangente bude u jedinici. (Ponovno, ako sam ja to sve sad dobro izračunao.) Dakle, sad želiš da kut između ove dvije tangente bude 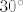 . E, sad si nacrtaj to na papiru ili što već: dobivaš da druga krivulja mora imati kut . E, sad si nacrtaj to na papiru ili što već: dobivaš da druga krivulja mora imati kut 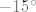 ili ili 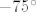 obzirom na obzirom na  os. No, onda mora dakle biti os. No, onda mora dakle biti 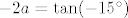 ili ili 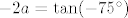 . Dakle, . Dakle, 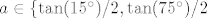 . Naglašavam, račun nisam provjeravao, tako da je sasvim moguće kriv, ali to bi bila ideja. Rezultat se, čak i ako je točan, sigurno može zapisati i ljepše. . Naglašavam, račun nisam provjeravao, tako da je sasvim moguće kriv, ali to bi bila ideja. Rezultat se, čak i ako je točan, sigurno može zapisati i ljepše. 
Nadam se da je bilo od pomoći. 
EDIT: Joker, hvala na ispravki. 
Zadnja promjena: mornik; 7:16 ned, 3. 4. 2011; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 6:31 pet, 1. 4. 2011 Naslov: Postano: 6:31 pet, 1. 4. 2011 Naslov: |
    |
|
|
Ajd' da probamo ovako: primijeti da je to zapravo [latex]-2\sin(x^2)\ln(x)[/latex], a to je [latex]-2\displaystyle\frac{\sin(x^2)}{x^2}\ln(x)x^2[/latex], nas zapravo samo zanima limes od [latex]x^2\ln(x)[/latex]. To je jednako, ako se ne varam, [latex]-\displaystyle\frac{\ln(1/x)}{1/x^2}[/latex], tj. uz supstituciju [latex]t=1/x[/latex] zanima nas limes of [latex]-\displaystyle\frac{\ln(t)}{t^2}[/latex] za [latex]t\to +\infty[/latex]. Ovo sad napadni L'Hôpitalom i brzo će se predati. :D Limes je, dakle, zbilja [latex]0[/latex]. :)
Ajd' da probamo ovako: primijeti da je to zapravo 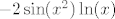 , a to je , a to je 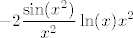 , nas zapravo samo zanima limes od , nas zapravo samo zanima limes od 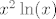 . To je jednako, ako se ne varam, . To je jednako, ako se ne varam, 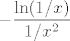 , tj. uz supstituciju , tj. uz supstituciju 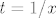 zanima nas limes of zanima nas limes of 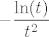 za za 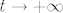 . Ovo sad napadni L'Hôpitalom i brzo će se predati. . Ovo sad napadni L'Hôpitalom i brzo će se predati.  Limes je, dakle, zbilja Limes je, dakle, zbilja  . . 
|
|
| [Vrh] |
|
Joker
Forumaš(ica)

Pridružen/a: 19. 09. 2010. (10:19:16)
Postovi: (8C)16
Spol: 
|
 Postano: 8:48 sub, 2. 4. 2011 Naslov: Postano: 8:48 sub, 2. 4. 2011 Naslov: |
    |
|
|
[quote="mornik"]Evo, samo na brzinu: u vezi trećeg zadatka, primijeti da je [latex]0\leq|f(x)|=|\ln x\cdot\cos(\frac{1}{x-1})\leq|\ln x|[/latex], a za [latex]x\to 1[/latex], [latex]\ln x\to 0[/latex]. Stoga, traženi limes za [latex]x\to 1[/latex] je [latex]0[/latex]. Sad, dakle, dodefiniramo [latex]f(1)=0[/latex]. Takva funkcija nije neprekidno derivabilna. Dapače, ona nije ni derivabilna u [latex]1[/latex]. Pogledajmo što je [latex]\displaystyle\frac{f(x)-f(1)}{x-1}[/latex]. To je [latex]\displaystyle\frac{\ln x}{x-1}\cos(\frac{1}{x-1})[/latex]. Budući da za [latex]x\to 1[/latex] vrijedi [latex]\frac{\ln x}{x-1}\to 1[/latex], a [latex]\cos(\frac{1}{x-1})[/latex] nema limes za [latex]x\to 1[/latex] (Kad kosinus "ide u beskonačno", i dalje postiže i jedinice i [latex]-1[/latex], tako da nikako ne konvergira. Ovo se, dakako, može i formalnije napisati. :)), ništa od toga. :D
Što se četvrtog tiče, prvo ćemo odrediti koliki su [latex]x[/latex] i [latex]y[/latex]. Iz prve jednadžbe imamo [latex]y=\frac{2}{\sqrt{x}}[/latex], a uvrštavanjem u drugu dobivamo [latex]x^{a-1/2}=1[/latex], tj. [latex]x=1[/latex]. [b]Dakle, radi se o točki [latex](1,1)[/latex].[/b] Sad pogledajmo koji je koeficijent smjera tangenata ove dvije kružnice u tim točkama: za prvu imamo, ako sam ja to sad točno na brzinu izračunao, [latex]y'=\frac{-1}{x^{-3/2}}[/latex], tj. [latex]y'=-1[/latex] u našoj točki. Za drugu imamo valjda [latex]y'=\frac{-2a}{x^{a+1}}[/latex], odnosno [latex]y'=-2a[/latex] u jedinici. (Ponovno, ako sam ja to sve sad dobro izračunao.) Dakle, sad želiš da kut između ove dvije tangente bude [latex]30^\circ[/latex]. E, sad si nacrtaj to na papiru ili što već: dobivaš da druga krivulja mora imati kut [latex]-15^\circ[/latex] ili [latex]-75^\circ[/latex] obzirom na [latex]x[/latex] os. No, onda mora dakle biti [latex]-2a=\tan(-15^\circ)[/latex] ili [latex]-2a=\tan(-75^\circ)[/latex]. Dakle, [latex]a\in\{\tan(15^\circ)/2, \tan(75^\circ)/2[/latex]. Naglašavam, račun nisam provjeravao, tako da je sasvim moguće kriv, ali to bi bila ideja. Rezultat se, čak i ako je točan, sigurno može zapisati i ljepše. :)
Nadam se da je bilo od pomoći. :)[/quote]
jel tocka mozda (1,2) onda? falio mi je ovaj bezazleni zakljucak da x mora biti 1 ili je a 1/2? hvala
| mornik (napisa): | Evo, samo na brzinu: u vezi trećeg zadatka, primijeti da je 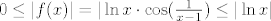 , a za , a za 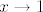 , , 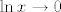 . Stoga, traženi limes za . Stoga, traženi limes za 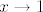 je je  . Sad, dakle, dodefiniramo . Sad, dakle, dodefiniramo 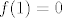 . Takva funkcija nije neprekidno derivabilna. Dapače, ona nije ni derivabilna u . Takva funkcija nije neprekidno derivabilna. Dapače, ona nije ni derivabilna u  . Pogledajmo što je . Pogledajmo što je 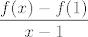 . To je . To je 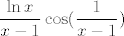 . Budući da za . Budući da za 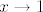 vrijedi vrijedi 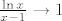 , a , a 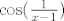 nema limes za nema limes za 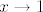 (Kad kosinus "ide u beskonačno", i dalje postiže i jedinice i (Kad kosinus "ide u beskonačno", i dalje postiže i jedinice i  , tako da nikako ne konvergira. Ovo se, dakako, može i formalnije napisati. , tako da nikako ne konvergira. Ovo se, dakako, može i formalnije napisati.  ), ništa od toga. ), ništa od toga. 
Što se četvrtog tiče, prvo ćemo odrediti koliki su  i i  . Iz prve jednadžbe imamo . Iz prve jednadžbe imamo 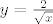 , a uvrštavanjem u drugu dobivamo , a uvrštavanjem u drugu dobivamo 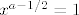 , tj. , tj.  . Dakle, radi se o točki . Dakle, radi se o točki 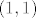 . Sad pogledajmo koji je koeficijent smjera tangenata ove dvije kružnice u tim točkama: za prvu imamo, ako sam ja to sad točno na brzinu izračunao, . Sad pogledajmo koji je koeficijent smjera tangenata ove dvije kružnice u tim točkama: za prvu imamo, ako sam ja to sad točno na brzinu izračunao, 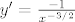 , tj. , tj.  u našoj točki. Za drugu imamo valjda u našoj točki. Za drugu imamo valjda 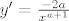 , odnosno , odnosno 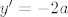 u jedinici. (Ponovno, ako sam ja to sve sad dobro izračunao.) Dakle, sad želiš da kut između ove dvije tangente bude u jedinici. (Ponovno, ako sam ja to sve sad dobro izračunao.) Dakle, sad želiš da kut između ove dvije tangente bude 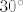 . E, sad si nacrtaj to na papiru ili što već: dobivaš da druga krivulja mora imati kut . E, sad si nacrtaj to na papiru ili što već: dobivaš da druga krivulja mora imati kut 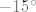 ili ili 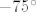 obzirom na obzirom na  os. No, onda mora dakle biti os. No, onda mora dakle biti 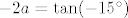 ili ili 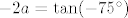 . Dakle, . Dakle, 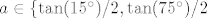 . Naglašavam, račun nisam provjeravao, tako da je sasvim moguće kriv, ali to bi bila ideja. Rezultat se, čak i ako je točan, sigurno može zapisati i ljepše. . Naglašavam, račun nisam provjeravao, tako da je sasvim moguće kriv, ali to bi bila ideja. Rezultat se, čak i ako je točan, sigurno može zapisati i ljepše. 
Nadam se da je bilo od pomoći.  |
jel tocka mozda (1,2) onda? falio mi je ovaj bezazleni zakljucak da x mora biti 1 ili je a 1/2? hvala
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
|
| [Vrh] |
|
|








