| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
michelangelo
Forumaš(ica)

Pridružen/a: 25. 06. 2009. (22:59:23)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
michelangelo
Forumaš(ica)

Pridružen/a: 25. 06. 2009. (22:59:23)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
Boris B.
Forumaš(ica)

Pridružen/a: 19. 01. 2010. (18:01:54)
Postovi: (32)16
Spol: 
|
 Postano: 22:15 pet, 25. 3. 2011 Naslov: Re: vježbe za kolokvij Postano: 22:15 pet, 25. 3. 2011 Naslov: Re: vježbe za kolokvij |
    |
|
|
[quote="michelangelo"]kako se rješavaju zadaci tipa odredi [latex]\mathrm{Int}(\mathbb{Z}_{9})[/latex] ili [latex]\mathrm{Aut}(\mathbb{Z}_{9})[/latex] ???? tnx unaprijed[/quote]
Kako je Z9 komutativna, Int(Z9) je trivijalna (a + x - a = x, za svako x i za svako a).
Aut(Z9) određuješ po tome što automorfizmi kao i svi monomorfizmi čuvaju red elementa, pa posebno i generatore prevode u generatore, a za cikličku grupu je homomorfizam potpuno određen djelovanjem na generatoru.
Dakle odabereš proizvoljan generator Z9 (npr. 1) i popišeš sve moguće načine da ga pošalješ u neki generator Z9. Kako su oni {1, 2, 4, 5, 7, 8} (brojevi manji od 9, a s 9 relativno prosti), Aut(Z9) se sastoji od fi(9) = 6 funkcija, nazovimo ih f1, f2, f4, f5, f7, f8.
Nadalje, lako se provjeri da je za cikličku grupu grupa automorfizama komutativna, pa možeš primijeniti teorem o strukturi konačnih Abelovih grupa, koji u ovom slučaju daje [latex]\mathbb Z/2 \mathbb Z \oplus \mathbb Z/3 \mathbb Z \cong \mathbb Z/6 \mathbb Z[/latex] kao jedinu komutativnu grupu reda 6, pa znamo da je riječ o njoj. Inače, ako postoji više komutativnih grupa koje dolaze u obzir, onda ispitaš redove elemenata u grupi automorfizama kako bi saznao o čemu se radi.
Npr. za Aut(Z5) bi imao fi(5) = 4 automorfizma, a postoje dvije komutativne grupe reda 4: Z/2Z + Z/2Z i Z/4Z. No u prvoj grupi su svi elementi osim jediničnoga reda 2, a u drugoj su [1] i [3] reda 4, pa to možemo usporediti s redovima elemenata u grupi automorfizama.
Neka su oni s f1, f2, f3 i f4 (dani s fi(1) = i). Kako je npr. f(f(2)) = 4, vidimo da je red od f2 > 2, pa grupa automorfizama mora biti Z/4Z.
| michelangelo (napisa): | kako se rješavaju zadaci tipa odredi 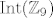 ili ili 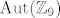 ???? tnx unaprijed ???? tnx unaprijed |
Kako je Z9 komutativna, Int(Z9) je trivijalna (a + x - a = x, za svako x i za svako a).
Aut(Z9) određuješ po tome što automorfizmi kao i svi monomorfizmi čuvaju red elementa, pa posebno i generatore prevode u generatore, a za cikličku grupu je homomorfizam potpuno određen djelovanjem na generatoru.
Dakle odabereš proizvoljan generator Z9 (npr. 1) i popišeš sve moguće načine da ga pošalješ u neki generator Z9. Kako su oni {1, 2, 4, 5, 7, 8} (brojevi manji od 9, a s 9 relativno prosti), Aut(Z9) se sastoji od fi(9) = 6 funkcija, nazovimo ih f1, f2, f4, f5, f7, f8.
Nadalje, lako se provjeri da je za cikličku grupu grupa automorfizama komutativna, pa možeš primijeniti teorem o strukturi konačnih Abelovih grupa, koji u ovom slučaju daje 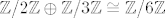 kao jedinu komutativnu grupu reda 6, pa znamo da je riječ o njoj. Inače, ako postoji više komutativnih grupa koje dolaze u obzir, onda ispitaš redove elemenata u grupi automorfizama kako bi saznao o čemu se radi. kao jedinu komutativnu grupu reda 6, pa znamo da je riječ o njoj. Inače, ako postoji više komutativnih grupa koje dolaze u obzir, onda ispitaš redove elemenata u grupi automorfizama kako bi saznao o čemu se radi.
Npr. za Aut(Z5) bi imao fi(5) = 4 automorfizma, a postoje dvije komutativne grupe reda 4: Z/2Z + Z/2Z i Z/4Z. No u prvoj grupi su svi elementi osim jediničnoga reda 2, a u drugoj su [1] i [3] reda 4, pa to možemo usporediti s redovima elemenata u grupi automorfizama.
Neka su oni s f1, f2, f3 i f4 (dani s fi(1) = i). Kako je npr. f(f(2)) = 4, vidimo da je red od f2 > 2, pa grupa automorfizama mora biti Z/4Z.
_________________
The lyf so short, the craft so long to lerne
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Boris B.
Forumaš(ica)

Pridružen/a: 19. 01. 2010. (18:01:54)
Postovi: (32)16
Spol: 
|
 Postano: 21:13 sub, 26. 3. 2011 Naslov: Postano: 21:13 sub, 26. 3. 2011 Naslov: |
    |
|
|
@Anchy: Int G je trivijalna za sve Abelove grupe, tako da da.
Za Aut G, oznacimo s fi homomorfizam za koji je f(1) = i.
Tada je Aut Z10 = {f1, f3, f7, f9}.
Da je Aut Z10 ~= Z2 + Z2, tada bi te cetiri funkcije komponirane same sa sobom morale biti jednake identiteti, tj. reda najvise 2, jer su takvi svi elementi u Z2 + Z2.
No to nije slucaj: f3 * f3 = f9 (jer je f3(f3(1)) = 9). Dakle, Aut Z10 mora biti izomorfna Z4.
@Smajl: Jel treba jos odgovor za 4a)? To ide relativno jednostavno, mozes samo pretpostaviti suprotno.
@Anchy: Int G je trivijalna za sve Abelove grupe, tako da da.
Za Aut G, oznacimo s fi homomorfizam za koji je f(1) = i.
Tada je Aut Z10 = {f1, f3, f7, f9}.
Da je Aut Z10 ~= Z2 + Z2, tada bi te cetiri funkcije komponirane same sa sobom morale biti jednake identiteti, tj. reda najvise 2, jer su takvi svi elementi u Z2 + Z2.
No to nije slucaj: f3 * f3 = f9 (jer je f3(f3(1)) = 9). Dakle, Aut Z10 mora biti izomorfna Z4.
@Smajl: Jel treba jos odgovor za 4a)? To ide relativno jednostavno, mozes samo pretpostaviti suprotno.
_________________
The lyf so short, the craft so long to lerne
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
pipi
Forumaš(ica)

Pridružen/a: 24. 06. 2010. (19:16:56)
Postovi: (15)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 23:00 sub, 26. 3. 2011 Naslov: Postano: 23:00 sub, 26. 3. 2011 Naslov: |
    |
|
|
Mozes odmah rec da je G ciklicka, jer je produkt Z-ova koji su relativno prosti (a za takve uvijek znas da su ciklicke). Npr, (1,1,1) generira svih 60 elemenata - to je tzv. kineski teorem o ostacima (uvijek zvuci ko nesto s TV prodaje... :D).
Kad se trazi izomorfizam s drugom grupom, dovoljno je poslati generator u generator, pa bi homomorfizam f bio izomorfizam ako definiramo
f(1,1,1)=1
(ovo, zbog toga sto je f izomorfizam, definira sve ostale funkcijske vrijednosti)
Opcenito, Aut(Zn) nije ciklicka. (Uvijek je Abelova zbog onog sta smo pokazali na vjezbama, al ciklicka nije...)
Npr: Z8 ima 4 automorfizma. (fi(8 )=4)
[latex]f_1(1)=1 \Rightarrow[/latex] to je identiteta, dakle red tog elementa je 1
[latex]f_2(1)=3 \Rightarrow f_2^2(1)=1[/latex] (red elementa je 2)
[latex]f_3(1)=5 \Rightarrow f_3^2(1)=1[/latex] (opet 2)
[latex]f_4(1)=7 \Rightarrow f_4^2(1)=1[/latex] (takodjer 2)
=> Aut(Z8 ) nema element reda 4, pa grupa nije ciklicka.
Ako je n prost, onda je Aut(Zn) ciklicka.
za Z10, Aut je ciklicka:
npr, ak uzmemo f homomorfizam t.d. f(1)=3, on je generator:
f^2(1)=9
f^3(1)=27=7
f^4(1)=1
(dakle komponiranjem f-a sa samim sobom dobijemo sve ostale automorfizme - dovoljno je pokazati da se 1 moze slikati u sve generatore grupe Z10)
@smajl: Ono stvarno je grupa:
zatvorenost je ocita;
asocijativnost naslijedjena
neutral isto
inverz - znamo da postoji, al pitanje je dal mu je 3 fiksna tocka.
kad bi bilo f^-1(3) = x, onda je ocito f(f^-1(3))=x, a znamo f(f^-1(3))=id(3)=3, pa zakljucujemo x=3.
Sto se tice ovih podgrupa, 7 ne postoji jer 7 ne dijeli 5!,
5 i 4 postoje (za 5 je samo shift za jedno mjesto primjer:
1,2,3,4,5 -> 5,1,2,3,4 (ciklicka grupa generirana ovim elementom je reda 5)
za 4:
1,5,2,3,4 (ovo ima ciklus duljine 4, pa i ciklicka grupa generirana s tim ima 4 elementa)
p.s. smajlic 8) bi fakat trebalo ukinut, ne mozes 8 napisat bez da te zaskoci :D
Mozes odmah rec da je G ciklicka, jer je produkt Z-ova koji su relativno prosti (a za takve uvijek znas da su ciklicke). Npr, (1,1,1) generira svih 60 elemenata - to je tzv. kineski teorem o ostacima (uvijek zvuci ko nesto s TV prodaje...  ). ).
Kad se trazi izomorfizam s drugom grupom, dovoljno je poslati generator u generator, pa bi homomorfizam f bio izomorfizam ako definiramo
f(1,1,1)=1
(ovo, zbog toga sto je f izomorfizam, definira sve ostale funkcijske vrijednosti)
Opcenito, Aut(Zn) nije ciklicka. (Uvijek je Abelova zbog onog sta smo pokazali na vjezbama, al ciklicka nije...)
Npr: Z8 ima 4 automorfizma. (fi(8 )=4)
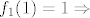 to je identiteta, dakle red tog elementa je 1 to je identiteta, dakle red tog elementa je 1
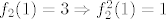 (red elementa je 2) (red elementa je 2)
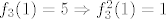 (opet 2) (opet 2)
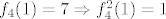 (takodjer 2) (takodjer 2)
⇒ Aut(Z8 ) nema element reda 4, pa grupa nije ciklicka.
Ako je n prost, onda je Aut(Zn) ciklicka.
za Z10, Aut je ciklicka:
npr, ak uzmemo f homomorfizam t.d. f(1)=3, on je generator:
f^2(1)=9
f^3(1)=27=7
f^4(1)=1
(dakle komponiranjem f-a sa samim sobom dobijemo sve ostale automorfizme - dovoljno je pokazati da se 1 moze slikati u sve generatore grupe Z10)
@smajl: Ono stvarno je grupa:
zatvorenost je ocita;
asocijativnost naslijedjena
neutral isto
inverz - znamo da postoji, al pitanje je dal mu je 3 fiksna tocka.
kad bi bilo f^-1(3) = x, onda je ocito f(f^-1(3))=x, a znamo f(f^-1(3))=id(3)=3, pa zakljucujemo x=3.
Sto se tice ovih podgrupa, 7 ne postoji jer 7 ne dijeli 5!,
5 i 4 postoje (za 5 je samo shift za jedno mjesto primjer:
1,2,3,4,5 → 5,1,2,3,4 (ciklicka grupa generirana ovim elementom je reda 5)
za 4:
1,5,2,3,4 (ovo ima ciklus duljine 4, pa i ciklicka grupa generirana s tim ima 4 elementa)
p.s. smajlic  bi fakat trebalo ukinut, ne mozes 8 napisat bez da te zaskoci bi fakat trebalo ukinut, ne mozes 8 napisat bez da te zaskoci 
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 7:44 ned, 27. 3. 2011 Naslov: Postano: 7:44 ned, 27. 3. 2011 Naslov: |
    |
|
|
[quote=".anchy."]
http://web.math.hr/nastava/alg/zadace/zadaca4.pdf
kako bi išli 7. i 10.zad? s time da u 7.znam dokazati da je normalna na ruke,ali mi to bude previše množenja), a 10.zadatak jer mi ti teoremi o izomorfizmima nisu jasni baš,a o dokazima istih da ne pričam(za 2. i 3.) :D
/[/quote]
može 7.? sjetila sam se da je to kao mali dio(onaj dio koji je u Z12) od 4Z,pa je komutativna(?) i iz tog razloga normalna podgrupa? :?:
samo prvo treba provjeriti da je podgrupa..to standardno?
kako još mogu zaključiti da je nešto normalna podgrupa,osim provjeravanja po def?
| .anchy. (napisa): |
http://web.math.hr/nastava/alg/zadace/zadaca4.pdf
kako bi išli 7. i 10.zad? s time da u 7.znam dokazati da je normalna na ruke,ali mi to bude previše množenja), a 10.zadatak jer mi ti teoremi o izomorfizmima nisu jasni baš,a o dokazima istih da ne pričam(za 2. i 3.) 
/ |
može 7.? sjetila sam se da je to kao mali dio(onaj dio koji je u Z12) od 4Z,pa je komutativna(?) i iz tog razloga normalna podgrupa? 
samo prvo treba provjeriti da je podgrupa..to standardno?
kako još mogu zaključiti da je nešto normalna podgrupa,osim provjeravanja po def?
|
|
| [Vrh] |
|
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
ante c
Forumaš(ica)


Pridružen/a: 10. 10. 2009. (19:18:15)
Postovi: (62)16
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
Boris B.
Forumaš(ica)

Pridružen/a: 19. 01. 2010. (18:01:54)
Postovi: (32)16
Spol: 
|
 Postano: 13:56 ned, 27. 3. 2011 Naslov: Postano: 13:56 ned, 27. 3. 2011 Naslov: |
    |
|
|
@Ante c.
Nije, [2] *(6) [3] = [0].
@pajopatak:
Da je ciklicka, morao bi postojati element reda 9, a ovdje su svi reda <= 3. Naime, elementi Z3 + Z3 su oblika (a, b) gdje su a i b iz Z3, pa je po definiciji mnozenja na direktnoj sumi (a, b)^3 = (a^3, b^3) = (0, 0).
@Ante c.
Nije, [2] *(6) [3] = [0].
@pajopatak:
Da je ciklicka, morao bi postojati element reda 9, a ovdje su svi reda ⇐ 3. Naime, elementi Z3 + Z3 su oblika (a, b) gdje su a i b iz Z3, pa je po definiciji mnozenja na direktnoj sumi (a, b)^3 = (a^3, b^3) = (0, 0).
_________________
The lyf so short, the craft so long to lerne
|
|
| [Vrh] |
|
|















