| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
__fox
Forumaš(ica)


Pridružen/a: 28. 11. 2008. (20:00:38)
Postovi: (35)16
Spol: 
|
|
| [Vrh] |
|
PopStevo
Forumaš(ica)

Pridružen/a: 24. 08. 2007. (12:40:28)
Postovi: (42)16
Spol: 
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
finalni
Forumaš(ica)


Pridružen/a: 04. 08. 2007. (11:48:53)
Postovi: (10D)16
Spol: 
Lokacija: Bloodbuzz Zagreb
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
 Postano: 11:58 pon, 19. 4. 2010 Naslov: Postano: 11:58 pon, 19. 4. 2010 Naslov: |
    |
|
|
[i]Pomalo, vrag odnija prišu[/i] :weee:
Nego, je l` riješena misterija oko dodatnih i nedodatnih bodova?
Po jednom profesoru su dodatni, po drugom nisu, a mene jako zanima koliko bodova smijem izgubit na 2. kolokviju i trebam li se trudit za 2. blic pošto ne planiram u primjenjene vode pa mi nije bitno baš da sve naučim pa se ne bi previše zamarala pa usput pišem duge rečenice jer mi se onako usput ne da učit za kolokvij ovaj tjedan jer je lijepo vrijeme i kava me zove i tako to.
Pomalo, vrag odnija prišu 
Nego, je l` riješena misterija oko dodatnih i nedodatnih bodova?
Po jednom profesoru su dodatni, po drugom nisu, a mene jako zanima koliko bodova smijem izgubit na 2. kolokviju i trebam li se trudit za 2. blic pošto ne planiram u primjenjene vode pa mi nije bitno baš da sve naučim pa se ne bi previše zamarala pa usput pišem duge rečenice jer mi se onako usput ne da učit za kolokvij ovaj tjedan jer je lijepo vrijeme i kava me zove i tako to.
_________________ mladac: e.k.s. je možda 8%, moje znanje ni toliko  |
|
| [Vrh] |
|
Gost
|
 Postano: 12:18 pon, 19. 4. 2010 Naslov: Postano: 12:18 pon, 19. 4. 2010 Naslov: |
    |
|
|
[quote="Masiela"]
Nego, je l` riješena misterija oko dodatnih i nedodatnih bodova?
[b]Po jednom profesoru su dodatni, po drugom nisu[/b],...[/quote]
"po oba" profesora [b]ne postoji[/b] tako nesto poput [b]dodatnih bodova[/b], sve su to "regularni bodovi", samo sto ovaj put "skala" ne ide do 100, nego do 112
nadam se je to sad malo jasnije ;)
| Masiela (napisa): |
Nego, je l` riješena misterija oko dodatnih i nedodatnih bodova?
Po jednom profesoru su dodatni, po drugom nisu,... |
"po oba" profesora ne postoji tako nesto poput dodatnih bodova, sve su to "regularni bodovi", samo sto ovaj put "skala" ne ide do 100, nego do 112
nadam se je to sad malo jasnije 
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
PopStevo
Forumaš(ica)

Pridružen/a: 24. 08. 2007. (12:40:28)
Postovi: (42)16
Spol: 
|
|
| [Vrh] |
|
finalni
Forumaš(ica)


Pridružen/a: 04. 08. 2007. (11:48:53)
Postovi: (10D)16
Spol: 
Lokacija: Bloodbuzz Zagreb
|
|
| [Vrh] |
|
ivica13
Forumaš(ica)

Pridružen/a: 03. 10. 2007. (14:01:02)
Postovi: (102)16
Spol: 
|
|
| [Vrh] |
|
finalni
Forumaš(ica)


Pridružen/a: 04. 08. 2007. (11:48:53)
Postovi: (10D)16
Spol: 
Lokacija: Bloodbuzz Zagreb
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
muttley
Forumaš(ica)
Pridružen/a: 07. 11. 2008. (12:31:55)
Postovi: (23)16
Spol: 
|
|
| [Vrh] |
|
nike
Forumaš(ica)

Pridružen/a: 11. 02. 2010. (13:05:01)
Postovi: (58)16
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 22:51 pon, 28. 3. 2011 Naslov: Postano: 22:51 pon, 28. 3. 2011 Naslov: |
    |
|
|
Evo npr. iz 2009.
[latex]\Phi\left(\mathbf{x}\right)=\int\limits_{0}^{\frac{\pi}{2}}\left(x'_1^2\left(t\right)+x'_2^2\left(t\right)+x'_3^2\left(t\right)-x_1^2\left(t\right)-x_2^2\left(t\right)-2x_3\left(t\right)\right)dt,[/latex]
(ne funkcionira naredba "\overdot"...)
[latex]x_1\left(0\right)=1,\, x_1\left(\frac{\pi}{2}\right)=0,\ x_2\left(0\right)=0,\, x_2\left(\frac{\pi}{2}\right)=1,\ x_3\left(0\right)=0,\, x_3\left(\frac{\pi}{2}\right)=-\frac{\pi^2}{8}[/latex].
Ekstremala mora zadovoljavati Euler - Lagrangeove jednadžbe:
[latex]\frac{d}{dt}\left(\frac{\partial F}{\partial x'_i}\right) - \frac{\partial F}{\partial x_i}=0[/latex], iz čega dobivamo ODJ:
[latex]2x_1''\left(t\right)+2x_1\left(t\right)=0,[/latex]
[latex]2x_2''\left(t\right)+2x_2\left(t\right)=0,[/latex]
[latex]2x_3''\left(t\right)+2=0.[/latex]
Rješavanjem dobivamo da je ekstremala
[latex]\mathbf{x}=\left(\cos\left(t\right),\, \sin\left(t\right), -\frac{t^2}{2}\right)[/latex].
Vrijednost zadanog funkcionala u njoj se lako računa i iznosi [latex]\frac{\pi^3}{12}[/latex].
Evo npr. iz 2009.
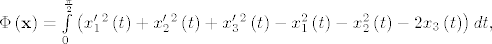
(ne funkcionira naredba "\overdot"...)
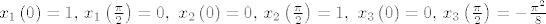 . .
Ekstremala mora zadovoljavati Euler - Lagrangeove jednadžbe:
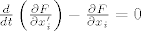 , iz čega dobivamo ODJ: , iz čega dobivamo ODJ:
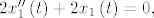
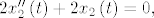
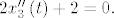
Rješavanjem dobivamo da je ekstremala
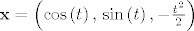 . .
Vrijednost zadanog funkcionala u njoj se lako računa i iznosi 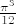 . .
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
tomitza
Forumaš(ica)


Pridružen/a: 28. 11. 2008. (19:50:48)
Postovi: (58)16
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
 Postano: 21:50 uto, 29. 3. 2011 Naslov: Postano: 21:50 uto, 29. 3. 2011 Naslov: |
    |
|
|
[quote="tomitza"]
ne brini se za peti, nece to doci posto nismo radili Bernoullijev princip... :)[/quote]
Pa, zapravo me to više veselilo nego brinulo :D , s obzirom na to da od teorije ne znam ništa a ovo se pojavilo prošla dva puta (pa sam mislio možda i treći)...
BTW, meni je svako rješenje (bilo raspisano, bilo samo konačni rezultat) od pomoći, jedino što baš znam je ono s ekstremalom. :D
| tomitza (napisa): |
ne brini se za peti, nece to doci posto nismo radili Bernoullijev princip...  |
Pa, zapravo me to više veselilo nego brinulo  , s obzirom na to da od teorije ne znam ništa a ovo se pojavilo prošla dva puta (pa sam mislio možda i treći)... , s obzirom na to da od teorije ne znam ništa a ovo se pojavilo prošla dva puta (pa sam mislio možda i treći)...
BTW, meni je svako rješenje (bilo raspisano, bilo samo konačni rezultat) od pomoći, jedino što baš znam je ono s ekstremalom. 
|
|
| [Vrh] |
|
|
















