Search
 
 
  Engleski
 
 
 
Open in this window (click to change)
Forum@DeGiorgi: Početna
Forum za podršku nastavi na PMF-MO
Login Registracija FAQ Smajlići Članstvo Pretražnik Forum@DeGiorgi: Početna

Zadace
WWW:
Idite na Prethodno  1, 2, 3, 4
Moja sarma
 
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Elementarna matematika 1 i 2
Prethodna tema :: Sljedeća tema  
Autor/ica Poruka
Phoenix
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
PostPostano: 20:17 uto, 29. 3. 2011    Naslov: Citirajte i odgovorite
Dokaži da su pravci [latex]A_{1}S[/latex], [latex]B_{1}S[/latex], [latex]C_{1}S[/latex] i [latex]D_{1}S[/latex] ([latex]A_{1}[/latex], [latex]B_{1}[/latex], [latex]C_{1}[/latex] i [latex]D_{1}[/latex] su točke koje promatramo) simetrale kuteva četverokuta kojeg promatramo. Iz toga bi slijedilo da je [latex]S[/latex] jednako udaljen od svakog kraka kuta, pa tako i od svake stranice četverokuta. Stoga bi tražena kružnica imala središte u točki [latex]S[/latex].
Dokaži da su pravc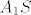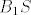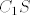i 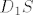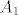, , 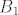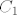i (, , i 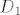su točke koje promatramo) simetrale kuteva četverokuta kojeg promatramo. Iz toga bi slijedilo da je jednako udaljen od svakog kraka kuta, pa tako i od svake stranice četverokuta. Stoga bi tražena kružnica imala središte u točki .


[Vrh]
Korisnički profil Pošaljite privatnu poruku
rurushu
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 29. 03. 2011. (18:33:06)
Postovi: (8)16
Sarma = la pohva - posuda
0 = 0 - 0
PostPostano: 21:48 uto, 29. 3. 2011    Naslov: Citirajte i odgovorite
Hvala!
Hvala!


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Annemarie
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 21. 10. 2010. (19:45:56)
Postovi: (62)16
Sarma = la pohva - posuda
-3 = 2 - 5
PostPostano: 13:25 uto, 26. 4. 2011    Naslov: Citirajte i odgovorite
Zna li netko možda kada će biti objavljena druga zadaća iz em2? Ako već nije... :?:
Zna li netko možda kada će biti objavljena druga zadaća iz em2? Ako već nije... Question


[Vrh]
Korisnički profil Pošaljite privatnu poruku
azra
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 01. 05. 2005. (08:23:56)
Postovi: (89)16
Sarma = la pohva - posuda
28 = 30 - 2
PostPostano: 16:33 čet, 12. 5. 2011    Naslov: Citirajte i odgovorite
Objavljena je druga sluzbena domaca zadaca. Tekst mozete naci ovdje:

http://web.math.hr/nastava/em/EM2/zadace/1011em2_dz2.pdf

Azra Tafro
Objavljena je druga sluzbena domaca zadaca. Tekst mozete naci ovdje:

http://web.math.hr/nastava/em/EM2/zadace/1011em2_dz2.pdf

Azra Tafro


[Vrh]
Korisnički profil Pošaljite privatnu poruku
kikzmyster
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: muško
Sarma = la pohva - posuda
45 = 46 - 1
PostPostano: 15:12 ned, 22. 5. 2011    Naslov: Citirajte i odgovorite
moze mali hint za 3. zadatak iz zadace?
moze mali hint za 3. zadatak iz zadace?


[Vrh]
Korisnički profil Pošaljite privatnu poruku
ceps
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
Sarma = la pohva - posuda
71 = 74 - 3
PostPostano: 16:40 ned, 22. 5. 2011    Naslov: Citirajte i odgovorite
Modul vektorskog produkta dvaju vektora je površina paralelograma koji je njima određen. Korištenjem toga i svojstava vektorskog produkta nije teško doći do rješenja. Reci ako treba nešto više.
Modul vektorskog produkta dvaju vektora je površina paralelograma koji je njima određen. Korištenjem toga i svojstava vektorskog produkta nije teško doći do rješenja. Reci ako treba nešto više.


[Vrh]
Korisnički profil Pošaljite privatnu poruku
kikzmyster
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: muško
Sarma = la pohva - posuda
45 = 46 - 1
PostPostano: 19:05 ned, 22. 5. 2011    Naslov: Citirajte i odgovorite
Znam to za vektorski produkt, ali ne znam, nikako ne mogu izvuc ovu trazenu povrsinu... ovaj cetverokut sto se trazi nije paralelogram, pa ne znam preko cega izrazit povrsinu
Znam to za vektorski produkt, ali ne znam, nikako ne mogu izvuc ovu trazenu povrsinu... ovaj cetverokut sto se trazi nije paralelogram, pa ne znam preko cega izrazit povrsinu


[Vrh]
Korisnički profil Pošaljite privatnu poruku
ceps
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
Sarma = la pohva - posuda
71 = 74 - 3
PostPostano: 20:38 ned, 22. 5. 2011    Naslov: Citirajte i odgovorite
Ne računaš odmah površinu tog paralelograma... Već imaš površinu trokuta ABC (i znaš da je 0.5 |(AB x AC)| = 30 ), kad nacrtaš sliku vidjet ćeš da treba od tog velikog trokuta ''odlomiti'' više ovih manjih da bi ostala površina četverokuta.
Pokušaj izraziti njihove stranice preko stranica velikog trokuta!

(jer znaš da vrijedi da je [latex](\alpha a \times b) = \alpha (a \times b)[/latex], za neki skalar [latex]\alpha[/latex] i [latex]a \times (b + c) = (a \times b) + (a \times c)[/latex])
Ne računaš odmah površinu tog paralelograma... Već imaš površinu trokuta ABC (i znaš da je 0.5 |(AB x AC)| = 30 ), kad nacrtaš sliku vidjet ćeš da treba od tog velikog trokuta ''odlomiti'' više ovih manjih da bi ostala površina četverokuta.
Pokušaj izraziti njihove stranice preko stranica velikog trokuta!

(jer znaš da vrijedi da je , za neki skalar i )


[Vrh]
Korisnički profil Pošaljite privatnu poruku
gtrup
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 05. 04. 2007. (12:42:58)
Postovi: (11)16
Sarma = la pohva - posuda
5 = 8 - 3
PostPostano: 21:21 ned, 22. 5. 2011    Naslov: Citirajte i odgovorite
Na web stranicama kolegija je objavljena treća domaća zadaća.

Goran Trupčević
Na web stranicama kolegija je objavljena treća domaća zadaća.

Goran Trupčević


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Lepi91
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: muško
Sarma = la pohva - posuda
9 = 13 - 4
PostPostano: 22:42 pon, 23. 5. 2011    Naslov: Citirajte i odgovorite
trecu predajemo na kolokviju?
trecu predajemo na kolokviju?



_________________
tko rano rani,malo spava
[Vrh]
Korisnički profil Pošaljite privatnu poruku
wannaknow
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 07. 09. 2010. (16:38:49)
Postovi: (2C)16
Sarma = la pohva - posuda
2 = 2 - 0
PostPostano: 15:31 sri, 1. 6. 2011    Naslov: Citirajte i odgovorite
[quote="Lepi91"]trecu predajemo na kolokviju?[/quote]

da

zna neko jel se za prolaz uključuju i bodovi iz zadaće ili se oni nadodaju samo u slučaju ako prođeš s bodovima prvog i drugog kolovija? zahvaljujem na odgovoru :)
Lepi91 (napisa):
trecu predajemo na kolokviju?


da

zna neko jel se za prolaz uključuju i bodovi iz zadaće ili se oni nadodaju samo u slučaju ako prođeš s bodovima prvog i drugog kolovija? zahvaljujem na odgovoru Smile



_________________
ljubav nije matematika...
[Vrh]
Korisnički profil Pošaljite privatnu poruku
Shaman
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 24. 09. 2011. (22:21:43)
Postovi: (76)16
Spol: muško
Sarma = la pohva - posuda
5 = 9 - 4
PostPostano: 15:59 ned, 25. 9. 2011    Naslov: Citirajte i odgovorite
[quote="pbakic"]Pa trebala bi se dokazati opcenita tvrdnja...
u a) dijelu, to znaci da treba raspisati opcenito, a u b) zadatku (ako se nasluti da tvrdnja ne vrijedi), dovoljno je naci konkretan kontraprimjer:
X={1,2} F={{1},{2}}
Y={2,3}, G={{2},{3}}
Sada imamo FuG={{1},{2},{3}}, a to je ocito particija skupa {1,2,3}=XuY,
ali X i Y nisu disjunktni. =>b) ne vrijedi.
Ako treba jos raspisati a), reci[/quote]

zar nije ako je X skup koji si napisao da je particija skupa X={{1},{2},{1,2},prazan skup}, a particija skupa Y={{2},{3},{2,3}, prazan skup}.
FuG={prazan skup,{1},{2},{1,2},{3},{4},{3,4}}.
a particija skupa XuY ima vise clanova kako su X i Y disjunktni skup ima 4 clanova, a particija onda 16 što nije jednako FuG kojeg sam gore napisao.
pbakic (napisa):
Pa trebala bi se dokazati opcenita tvrdnja...
u a) dijelu, to znaci da treba raspisati opcenito, a u b) zadatku (ako se nasluti da tvrdnja ne vrijedi), dovoljno je naci konkretan kontraprimjer:
X={1,2} F={{1},{2}}
Y={2,3}, G={{2},{3}}
Sada imamo FuG={{1},{2},{3}}, a to je ocito particija skupa {1,2,3}=XuY,
ali X i Y nisu disjunktni. ⇒b) ne vrijedi.
Ako treba jos raspisati a), reci


zar nije ako je X skup koji si napisao da je particija skupa X={{1},{2},{1,2},prazan skup}, a particija skupa Y={{2},{3},{2,3}, prazan skup}.
FuG={prazan skup,{1},{2},{1,2},{3},{4},{3,4}}.
a particija skupa XuY ima vise clanova kako su X i Y disjunktni skup ima 4 clanova, a particija onda 16 što nije jednako FuG kojeg sam gore napisao.


[Vrh]
Korisnički profil Pošaljite privatnu poruku
krcko
Forumaš nagrađen za životno djelo
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
Sarma = la pohva - posuda
655 = 759 - 104
PostPostano: 18:13 ned, 25. 9. 2011    Naslov: Citirajte i odgovorite
Ne mijesati particiju i partitivni skup :ccc:
Ne mijesati particiju i partitivni skup Ccc.... Sram te bilo...



_________________
Vedran Krcadinac

Ljudi su razliciti, a nula je paran broj.
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail Posjetite Web stranice
dalmatinčica
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
Sarma = la pohva - posuda
6 = 10 - 4
PostPostano: 18:51 sub, 1. 10. 2011    Naslov: Citirajte i odgovorite
aj raspišite pod a
:)
i 9.
aj raspišite pod a
Smile
i 9.


[Vrh]
Korisnički profil Pošaljite privatnu poruku
boksi
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 02. 09. 2011. (16:37:55)
Postovi: (44)16
Spol: žensko
Sarma = la pohva - posuda
0 = 0 - 0
PostPostano: 21:05 pet, 7. 10. 2011    Naslov: Citirajte i odgovorite
zanima me mogu li u sedmom zadatku iz zadaće ( [dtex] P(A)\setminus P(B)\subseteq P(A\setminus B) [/dtex] ) iskoristiti prazan skup kao protuprimjer ili nešto? jer prazan skup je član partitivnog skupa, a ne nalazi se u razlici?

ne znam uopće kako da to lijepo raspišem. :O
zanima me mogu li u sedmom zadatku iz zadaće ( [dtex] P(A)\setminus P(B)\subseteq P(A\setminus B) [/dtex] ) iskoristiti prazan skup kao protuprimjer ili nešto? jer prazan skup je član partitivnog skupa, a ne nalazi se u razlici?

ne znam uopće kako da to lijepo raspišem. :O


[Vrh]
Korisnički profil Pošaljite privatnu poruku
krcko
Forumaš nagrađen za životno djelo
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
Sarma = la pohva - posuda
655 = 759 - 104
PostPostano: 22:58 pet, 7. 10. 2011    Naslov: Citirajte i odgovorite
Mignon je dala iscrpne hintove u [url=http://degiorgi.math.hr/forum/viewtopic.php?t=17168]ovom topicu[/url], preporucam pogledati!
Mignon je dala iscrpne hintove u ovom topicu, preporucam pogledati!



_________________
Vedran Krcadinac

Ljudi su razliciti, a nula je paran broj.
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail Posjetite Web stranice
Prethodni postovi:   
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Elementarna matematika 1 i 2 Vremenska zona: GMT + 01:00.
Idite na Prethodno  1, 2, 3, 4
Stranica 4 / 4.

 
Forum(o)Bir:  
Ne možete otvarati nove teme.
Ne možete odgovarati na postove.
Ne možete uređivati Vaše postove.
Ne možete izbrisati Vaše postove.
Ne možete glasovati u anketama.
You can attach files in this forum
You can download files in this forum


Powered by phpBB © 2001, 2002 phpBB Group
Theme created by Vjacheslav Trushkin
HR (Cro) by Ančica Sečan