| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
zvonkec
Forumaš(ica)

Pridružen/a: 04. 11. 2010. (20:56:30)
Postovi: (37)16
Spol: 
|
 Postano: 19:19 sub, 2. 4. 2011 Naslov: Postano: 19:19 sub, 2. 4. 2011 Naslov: |
    |
|
|
[quote="frutabella"][quote="zvonkec"]Kako se dokaže da za svaki k postoji neka točka koju mozemo "fiksirat"?
Naravno, konkretne se vrijednosti ne mogu dobiti jer je k proizvoljan. Ideja je da ako je derivacija u nekoj točki (x,y) jednaka k, onda je i derivacija u točki (-x,-y) jednaka k, i dokaz je gotov, jer za proizvoljni k imamo dvije različite točke u kojima je derivacija jednaka k,tj, tangente u tim točkama su paralelne pravcu kx+l.
Ja sam u trećem zadatku dobio alfa=-1/2.Nadalje, što se tiće kritičnih točaka nije potrebno promatrati 0, jer smo tako "napravili" funkciju da je u 0 derivabilna, i [b]f'(0) nije nula pa 0 ne može biti ekstrem[/b]. No, ukoliko nismo sigurni, mislim da ne škodi uzet sve točke koje su nam "sumnjive",ništa se neće dogodit.Sto se tiće zadatka s korijenima ne vidim zašto funkcija ne bi bila derivabilna u 1 (mozda si nešto krivo prepisala),ali za 0 je jasno da smo je uzeli jer je nultočka (a nikad dovoljno opreza s nultočkama i korijenima).[/quote]
Hmm, sve razumijem, ali ovo podebljano bas i ne, ako te dobro razumijem, derivacija u bilo kojoj kriticnoj tocki bi trebala iznositi 0, da bi uopce mogli reci da je globalni min/max, a u ovom slucaju nasem ne znam bas kako bi to proslo...
ja dobila glob max = (114 + PI)/4, a buduci si rekao da je svejedno uzmemo li sve tocke kao "kriticne tocke" mislim da ovdje opet nije svjedeno, jer ako uzmemo da je 0 kriticna tocka onda glob min iznosi PI/4 (upravo taj f(0) ), a inace bi bio bez te 0, f(-1)= (10 + PI)/4.
Hvala na onom prvom pojasnjenom pitanju.
Jos me zanima: kako je lim (x-->1) [ ln(2x) - ln2 ] / [x-1]= 1 ??? :oops:[/quote]
Naravno da u globalnom ekstremu na nekom segmentu ne mora općenito derivacija biti nula, npr uzmi pravac y=x na segmentu npr. [0,1].
Što se tiće ovih minimuma i maksimuma neko je od nas dvoje krivo izračuno alfu ja sam dobio -1/2 pa možda zato dobivaš čudesa,treba provjerit to.:D
Dakle ono što je bitno: minimum na segmentu znaci najmanja vrijednost funkcije na tom segmentu, u točki tog minimuma ne mora čak ni postojati derivacija,pa čak funkcija ne mora ni biti neprekinuta u toj točki.Druga stvar je na otvorenim intervalima,tamo vrijedi Fermatova lema koja kaže da je u ekstremima derivacija jednaka 0.Također, ako gledamo funkciju na segmentu [a,b], te neki otvoreni podinterval <c,d> tog segmenta na kojem je funkcija derivabilna, na tim podintervalima vrijedi
Fermatova lema,tj. u točki e iz <c,d> je [b]lokalni[/b] ekstrem (dakle to je ekstrem samo za taj interval) ako i samo ako je f'(e)=0. Zato moramo sve te intervale,tj.točke u kojima funkcija nije derivabilna.Zatim naprosto pogledamo gdje je funkcija najveća: u nekom od lokalnih ekstrema koji smo izračunali ili u nekoj točki u kojoj funkcija nije derivabilna. Opet naglašavam, Fermatova lema vrijedi [b]samo na otvorenim intervalima[/b].
Eto ušo sam malo u teoriju nadam se da nisam naporan i još se više nadam da nisam nigdje fulo, a najviše se nadam da ti je sad nešto jasnije. :D
| frutabella (napisa): | | zvonkec (napisa): | Kako se dokaže da za svaki k postoji neka točka koju mozemo "fiksirat"?
Naravno, konkretne se vrijednosti ne mogu dobiti jer je k proizvoljan. Ideja je da ako je derivacija u nekoj točki (x,y) jednaka k, onda je i derivacija u točki (-x,-y) jednaka k, i dokaz je gotov, jer za proizvoljni k imamo dvije različite točke u kojima je derivacija jednaka k,tj, tangente u tim točkama su paralelne pravcu kx+l.
Ja sam u trećem zadatku dobio alfa=-1/2.Nadalje, što se tiće kritičnih točaka nije potrebno promatrati 0, jer smo tako "napravili" funkciju da je u 0 derivabilna, i f'(0) nije nula pa 0 ne može biti ekstrem. No, ukoliko nismo sigurni, mislim da ne škodi uzet sve točke koje su nam "sumnjive",ništa se neće dogodit.Sto se tiće zadatka s korijenima ne vidim zašto funkcija ne bi bila derivabilna u 1 (mozda si nešto krivo prepisala),ali za 0 je jasno da smo je uzeli jer je nultočka (a nikad dovoljno opreza s nultočkama i korijenima). |
Hmm, sve razumijem, ali ovo podebljano bas i ne, ako te dobro razumijem, derivacija u bilo kojoj kriticnoj tocki bi trebala iznositi 0, da bi uopce mogli reci da je globalni min/max, a u ovom slucaju nasem ne znam bas kako bi to proslo...
ja dobila glob max = (114 + PI)/4, a buduci si rekao da je svejedno uzmemo li sve tocke kao "kriticne tocke" mislim da ovdje opet nije svjedeno, jer ako uzmemo da je 0 kriticna tocka onda glob min iznosi PI/4 (upravo taj f(0) ), a inace bi bio bez te 0, f(-1)= (10 + PI)/4.
Hvala na onom prvom pojasnjenom pitanju.
Jos me zanima: kako je lim (x→1) [ ln(2x) - ln2 ] / [x-1]= 1 ???  |
Naravno da u globalnom ekstremu na nekom segmentu ne mora općenito derivacija biti nula, npr uzmi pravac y=x na segmentu npr. [0,1].
Što se tiće ovih minimuma i maksimuma neko je od nas dvoje krivo izračuno alfu ja sam dobio -1/2 pa možda zato dobivaš čudesa,treba provjerit to.
Dakle ono što je bitno: minimum na segmentu znaci najmanja vrijednost funkcije na tom segmentu, u točki tog minimuma ne mora čak ni postojati derivacija,pa čak funkcija ne mora ni biti neprekinuta u toj točki.Druga stvar je na otvorenim intervalima,tamo vrijedi Fermatova lema koja kaže da je u ekstremima derivacija jednaka 0.Također, ako gledamo funkciju na segmentu [a,b], te neki otvoreni podinterval <c,d> tog segmenta na kojem je funkcija derivabilna, na tim podintervalima vrijedi
Fermatova lema,tj. u točki e iz <c,d> je lokalni ekstrem (dakle to je ekstrem samo za taj interval) ako i samo ako je f'(e)=0. Zato moramo sve te intervale,tj.točke u kojima funkcija nije derivabilna.Zatim naprosto pogledamo gdje je funkcija najveća: u nekom od lokalnih ekstrema koji smo izračunali ili u nekoj točki u kojoj funkcija nije derivabilna. Opet naglašavam, Fermatova lema vrijedi samo na otvorenim intervalima.
Eto ušo sam malo u teoriju nadam se da nisam naporan i još se više nadam da nisam nigdje fulo, a najviše se nadam da ti je sad nešto jasnije. 
_________________
nekad sam bio umišljen al sam se promijenio sad sam savršen
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 20:09 sub, 2. 4. 2011 Naslov: Postano: 20:09 sub, 2. 4. 2011 Naslov: |
    |
|
|
[quote="zvonkec"][quote="frutabella"][quote="zvonkec"]Kako se dokaže da za svaki k postoji neka točka koju mozemo "fiksirat"?
Naravno, konkretne se vrijednosti ne mogu dobiti jer je k proizvoljan. Ideja je da ako je derivacija u nekoj točki (x,y) jednaka k, onda je i derivacija u točki (-x,-y) jednaka k, i dokaz je gotov, jer za proizvoljni k imamo dvije različite točke u kojima je derivacija jednaka k,tj, tangente u tim točkama su paralelne pravcu kx+l.
Ja sam u trećem zadatku dobio alfa=-1/2.Nadalje, što se tiće kritičnih točaka nije potrebno promatrati 0, jer smo tako "napravili" funkciju da je u 0 derivabilna, i [b]f'(0) nije nula pa 0 ne može biti ekstrem[/b]. No, ukoliko nismo sigurni, mislim da ne škodi uzet sve točke koje su nam "sumnjive",ništa se neće dogodit.Sto se tiće zadatka s korijenima ne vidim zašto funkcija ne bi bila derivabilna u 1 (mozda si nešto krivo prepisala),ali za 0 je jasno da smo je uzeli jer je nultočka (a nikad dovoljno opreza s nultočkama i korijenima).[/quote]
Hmm, sve razumijem, ali ovo podebljano bas i ne, ako te dobro razumijem, derivacija u bilo kojoj kriticnoj tocki bi trebala iznositi 0, da bi uopce mogli reci da je globalni min/max, a u ovom slucaju nasem ne znam bas kako bi to proslo...
ja dobila glob max = (114 + PI)/4, a buduci si rekao da je svejedno uzmemo li sve tocke kao "kriticne tocke" mislim da ovdje opet nije svjedeno, jer ako uzmemo da je 0 kriticna tocka onda glob min iznosi PI/4 (upravo taj f(0) ), a inace bi bio bez te 0, f(-1)= (10 + PI)/4.
Hvala na onom prvom pojasnjenom pitanju.
Jos me zanima: kako je lim (x-->1) [ ln(2x) - ln2 ] / [x-1]= 1 ??? :oops:[/quote]
Naravno da u globalnom ekstremu na nekom segmentu ne mora općenito derivacija biti nula, npr uzmi pravac y=x na segmentu npr. [0,1].
Što se tiće ovih minimuma i maksimuma neko je od nas dvoje krivo izračuno alfu ja sam dobio -1/2 pa možda zato dobivaš čudesa,treba provjerit to.:D
Dakle ono što je bitno: minimum na segmentu znaci najmanja vrijednost funkcije na tom segmentu, u točki tog minimuma ne mora čak ni postojati derivacija,pa čak funkcija ne mora ni biti neprekinuta u toj točki.Druga stvar je na otvorenim intervalima,tamo vrijedi Fermatova lema koja kaže da je u ekstremima derivacija jednaka 0.Također, ako gledamo funkciju na segmentu [a,b], te neki otvoreni podinterval <c,d> tog segmenta na kojem je funkcija derivabilna, na tim podintervalima vrijedi
Fermatova lema,tj. u točki e iz <c,d> je [b]lokalni[/b] ekstrem (dakle to je ekstrem samo za taj interval) ako i samo ako je f'(e)=0. Zato moramo sve te intervale,tj.točke u kojima funkcija nije derivabilna.Zatim naprosto pogledamo gdje je funkcija najveća: u nekom od lokalnih ekstrema koji smo izračunali ili u nekoj točki u kojoj funkcija nije derivabilna. Opet naglašavam, Fermatova lema vrijedi [b]samo na otvorenim intervalima[/b].
Eto ušo sam malo u teoriju nadam se da nisam naporan i još se više nadam da nisam nigdje fulo, a najviše se nadam da ti je sad nešto jasnije. :D[/quote]
Nije problem, hvala ti na strpljenju i pomoci. Sto se tice ove alfe, ne znam gdje sam mogla pogrijesiti: znaci funk je derivab u 0 ako postoje limesi s desna i lijeva u 0 i jednaki su
------> lim (0+) 1/ {1 + (1/[1+x])^2} = lim (0-) [-6x + ALFA]/1
------
-------> kad uvrstim tu 0, dobijem ALFA: 1/2. :cry:
Za globalne min/max gledam:
1) rubne tocke: -1, 3
2) nultocke derivacije: -1/12
3) i tocke u kojima funk, eventualno nije derivabilna: 1, 2 (0 smo rijesili)
I sad sve te tocke uvrstavamo u pocetnu funkciju (ne derivaciju) i procitamo min i max.
Hm, ako je to tocan postupak, opet cudne brojeve dobijem... :cry:
| zvonkec (napisa): | | frutabella (napisa): | | zvonkec (napisa): | Kako se dokaže da za svaki k postoji neka točka koju mozemo "fiksirat"?
Naravno, konkretne se vrijednosti ne mogu dobiti jer je k proizvoljan. Ideja je da ako je derivacija u nekoj točki (x,y) jednaka k, onda je i derivacija u točki (-x,-y) jednaka k, i dokaz je gotov, jer za proizvoljni k imamo dvije različite točke u kojima je derivacija jednaka k,tj, tangente u tim točkama su paralelne pravcu kx+l.
Ja sam u trećem zadatku dobio alfa=-1/2.Nadalje, što se tiće kritičnih točaka nije potrebno promatrati 0, jer smo tako "napravili" funkciju da je u 0 derivabilna, i f'(0) nije nula pa 0 ne može biti ekstrem. No, ukoliko nismo sigurni, mislim da ne škodi uzet sve točke koje su nam "sumnjive",ništa se neće dogodit.Sto se tiće zadatka s korijenima ne vidim zašto funkcija ne bi bila derivabilna u 1 (mozda si nešto krivo prepisala),ali za 0 je jasno da smo je uzeli jer je nultočka (a nikad dovoljno opreza s nultočkama i korijenima). |
Hmm, sve razumijem, ali ovo podebljano bas i ne, ako te dobro razumijem, derivacija u bilo kojoj kriticnoj tocki bi trebala iznositi 0, da bi uopce mogli reci da je globalni min/max, a u ovom slucaju nasem ne znam bas kako bi to proslo...
ja dobila glob max = (114 + PI)/4, a buduci si rekao da je svejedno uzmemo li sve tocke kao "kriticne tocke" mislim da ovdje opet nije svjedeno, jer ako uzmemo da je 0 kriticna tocka onda glob min iznosi PI/4 (upravo taj f(0) ), a inace bi bio bez te 0, f(-1)= (10 + PI)/4.
Hvala na onom prvom pojasnjenom pitanju.
Jos me zanima: kako je lim (x→1) [ ln(2x) - ln2 ] / [x-1]= 1 ???  |
Naravno da u globalnom ekstremu na nekom segmentu ne mora općenito derivacija biti nula, npr uzmi pravac y=x na segmentu npr. [0,1].
Što se tiće ovih minimuma i maksimuma neko je od nas dvoje krivo izračuno alfu ja sam dobio -1/2 pa možda zato dobivaš čudesa,treba provjerit to.
Dakle ono što je bitno: minimum na segmentu znaci najmanja vrijednost funkcije na tom segmentu, u točki tog minimuma ne mora čak ni postojati derivacija,pa čak funkcija ne mora ni biti neprekinuta u toj točki.Druga stvar je na otvorenim intervalima,tamo vrijedi Fermatova lema koja kaže da je u ekstremima derivacija jednaka 0.Također, ako gledamo funkciju na segmentu [a,b], te neki otvoreni podinterval <c,d> tog segmenta na kojem je funkcija derivabilna, na tim podintervalima vrijedi
Fermatova lema,tj. u točki e iz <c,d> je lokalni ekstrem (dakle to je ekstrem samo za taj interval) ako i samo ako je f'(e)=0. Zato moramo sve te intervale,tj.točke u kojima funkcija nije derivabilna.Zatim naprosto pogledamo gdje je funkcija najveća: u nekom od lokalnih ekstrema koji smo izračunali ili u nekoj točki u kojoj funkcija nije derivabilna. Opet naglašavam, Fermatova lema vrijedi samo na otvorenim intervalima.
Eto ušo sam malo u teoriju nadam se da nisam naporan i još se više nadam da nisam nigdje fulo, a najviše se nadam da ti je sad nešto jasnije.  |
Nije problem, hvala ti na strpljenju i pomoci. Sto se tice ove alfe, ne znam gdje sam mogla pogrijesiti: znaci funk je derivab u 0 ako postoje limesi s desna i lijeva u 0 i jednaki su
------> lim (0+) 1/ {1 + (1/[1+x])^2} = lim (0-) [-6x + ALFA]/1
------
-------> kad uvrstim tu 0, dobijem ALFA: 1/2. 
Za globalne min/max gledam:
1) rubne tocke: -1, 3
2) nultocke derivacije: -1/12
3) i tocke u kojima funk, eventualno nije derivabilna: 1, 2 (0 smo rijesili)
I sad sve te tocke uvrstavamo u pocetnu funkciju (ne derivaciju) i procitamo min i max.
Hm, ako je to tocan postupak, opet cudne brojeve dobijem... 
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 9:24 ned, 3. 4. 2011 Naslov: Postano: 9:24 ned, 3. 4. 2011 Naslov: |
    |
|
|
Opet pitanje u vezi iste stvari, drugi zadatak:
problem mi rade tocke u kojima funkcija nije derivabilna, kako ih odredit, ili se to pogađa, znam da je funk,derivabilna ako postoji limes u toj tocki, al u ovom primjeru, gdje treba naci sliku funkcije
f: [-5, 5] ---> R
f(x)= (x+2) / (x^2+4x+5)
provjeravam glob min/max u tockama -5, 5 (kao rubne), -1, -3 (kao nultocke prve derivacije), a sad one tockice u kojima nije derivabilna...ovako napamet ne znam kako bi to procijenila a da sam sigurna, a drugo sto mi pada, da isprobam vrijednost funcije u svim tockama između [-5, 5], tj, jos u -4, -2,
0, 1, 2, 3, 4 al i tu ima dosta posla.
Postoji li kakav kraci nacin?
ovaj mi se ne cini ispravnim, jer mi max ne ispada kao u Geogebri, po ovim mojim racunima trebao bi biti za x=-1, a po geogebri za x=2.
:roll:
Opet pitanje u vezi iste stvari, drugi zadatak:
problem mi rade tocke u kojima funkcija nije derivabilna, kako ih odredit, ili se to pogađa, znam da je funk,derivabilna ako postoji limes u toj tocki, al u ovom primjeru, gdje treba naci sliku funkcije
f: [-5, 5] → R
f(x)= (x+2) / (x^2+4x+5)
provjeravam glob min/max u tockama -5, 5 (kao rubne), -1, -3 (kao nultocke prve derivacije), a sad one tockice u kojima nije derivabilna...ovako napamet ne znam kako bi to procijenila a da sam sigurna, a drugo sto mi pada, da isprobam vrijednost funcije u svim tockama između [-5, 5], tj, jos u -4, -2,
0, 1, 2, 3, 4 al i tu ima dosta posla.
Postoji li kakav kraci nacin?
ovaj mi se ne cini ispravnim, jer mi max ne ispada kao u Geogebri, po ovim mojim racunima trebao bi biti za x=-1, a po geogebri za x=2.

|
|
| [Vrh] |
|
zvonkec
Forumaš(ica)

Pridružen/a: 04. 11. 2010. (20:56:30)
Postovi: (37)16
Spol: 
|
 Postano: 10:56 ned, 3. 4. 2011 Naslov: Postano: 10:56 ned, 3. 4. 2011 Naslov: |
    |
|
|
Prvo da se ispravim.U prošlom postu sam napisao slijedeće:
...u točki e iz <c,d> je lokalni ekstrem (dakle to je ekstrem samo za taj interval) ako i samo ako je f'(e)=0.
Naravno, to nije istina, naime ne vrijedi druga inkluzija,tj. ako f'(e)=0 ne mora u e biti ekstrem. Ispričavam se svima, najviše gospodinu Fermatu. :D
Nadalje, ako ne vidimo odmah u kojim točkama bi mogli imati problema s derivabilnosti, predlažem da naprosto funkciju izderiviramo i vidimo u kojim točkama domene derivacija ima prekid (obično je to lako uočiti). U tim točkama funkcija nije derivabilna i bok. No u ovakvim zadacima treba u biti samo provjeriti nultočke nazivnika. Ako ih nema tada je ustvari cijela funkcija produkt elementarnih funkcija, a znamo da je onda neprekinuta i derivabilna.
Specijalno, u ovom zadatku je funkcija , prema svemu rečenom, derivabilna na <-5,5> (naravno, ne možemo reći da je derivabilna na domeni kad je domena segment).Dakle, treba naći lokalne ekstreme na tom intervalu, te ih usporediti s vrijednostima funkcije u rubovima i to je to.
Prvo da se ispravim.U prošlom postu sam napisao slijedeće:
...u točki e iz <c,d> je lokalni ekstrem (dakle to je ekstrem samo za taj interval) ako i samo ako je f'(e)=0.
Naravno, to nije istina, naime ne vrijedi druga inkluzija,tj. ako f'(e)=0 ne mora u e biti ekstrem. Ispričavam se svima, najviše gospodinu Fermatu. 
Nadalje, ako ne vidimo odmah u kojim točkama bi mogli imati problema s derivabilnosti, predlažem da naprosto funkciju izderiviramo i vidimo u kojim točkama domene derivacija ima prekid (obično je to lako uočiti). U tim točkama funkcija nije derivabilna i bok. No u ovakvim zadacima treba u biti samo provjeriti nultočke nazivnika. Ako ih nema tada je ustvari cijela funkcija produkt elementarnih funkcija, a znamo da je onda neprekinuta i derivabilna.
Specijalno, u ovom zadatku je funkcija , prema svemu rečenom, derivabilna na <-5,5> (naravno, ne možemo reći da je derivabilna na domeni kad je domena segment).Dakle, treba naći lokalne ekstreme na tom intervalu, te ih usporediti s vrijednostima funkcije u rubovima i to je to.
_________________
nekad sam bio umišljen al sam se promijenio sad sam savršen
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 11:08 ned, 3. 4. 2011 Naslov: Postano: 11:08 ned, 3. 4. 2011 Naslov: |
    |
|
|
[quote="zvonkec"]Prvo da se ispravim.U prošlom postu sam napisao slijedeće:
...u točki e iz <c,d> je lokalni ekstrem (dakle to je ekstrem samo za taj interval) ako i samo ako je f'(e)=0.
Naravno, to nije istina, naime ne vrijedi druga inkluzija,tj. ako f'(e)=0 ne mora u e biti ekstrem. Ispričavam se svima, najviše gospodinu Fermatu. :D
Nadalje, ako ne vidimo odmah u kojim točkama bi mogli imati problema s derivabilnosti, predlažem da naprosto funkciju izderiviramo i vidimo u kojim točkama domene derivacija ima prekid (obično je to lako uočiti). U tim točkama funkcija nije derivabilna i bok. No u ovakvim zadacima treba u biti samo provjeriti nultočke nazivnika. Ako ih nema tada je ustvari cijela funkcija produkt elementarnih funkcija, a znamo da je onda neprekinuta i derivabilna.
Specijalno, u ovom zadatku je funkcija , prema svemu rečenom, derivabilna na <-5,5> (naravno, ne možemo reći da je derivabilna na domeni kad je domena segment).Dakle, treba naći lokalne ekstreme na tom intervalu, te ih usporediti s vrijednostima funkcije u rubovima i to je to.[/quote]
Aha, super. Hvala, ovo mi vec puno jasnije. :wink:
| zvonkec (napisa): | Prvo da se ispravim.U prošlom postu sam napisao slijedeće:
...u točki e iz <c,d> je lokalni ekstrem (dakle to je ekstrem samo za taj interval) ako i samo ako je f'(e)=0.
Naravno, to nije istina, naime ne vrijedi druga inkluzija,tj. ako f'(e)=0 ne mora u e biti ekstrem. Ispričavam se svima, najviše gospodinu Fermatu. 
Nadalje, ako ne vidimo odmah u kojim točkama bi mogli imati problema s derivabilnosti, predlažem da naprosto funkciju izderiviramo i vidimo u kojim točkama domene derivacija ima prekid (obično je to lako uočiti). U tim točkama funkcija nije derivabilna i bok. No u ovakvim zadacima treba u biti samo provjeriti nultočke nazivnika. Ako ih nema tada je ustvari cijela funkcija produkt elementarnih funkcija, a znamo da je onda neprekinuta i derivabilna.
Specijalno, u ovom zadatku je funkcija , prema svemu rečenom, derivabilna na ←5,5> (naravno, ne možemo reći da je derivabilna na domeni kad je domena segment).Dakle, treba naći lokalne ekstreme na tom intervalu, te ih usporediti s vrijednostima funkcije u rubovima i to je to. |
Aha, super. Hvala, ovo mi vec puno jasnije. 
|
|
| [Vrh] |
|
akolak
Forumaš(ica)

Pridružen/a: 27. 12. 2010. (16:52:59)
Postovi: (1D)16
|
 Postano: 16:09 ned, 3. 4. 2011 Naslov: Postano: 16:09 ned, 3. 4. 2011 Naslov: |
    |
|
|
[quote="Tomislav"]Hint: Izrazi y'. Fiksiraj k=k1 i neka su sada x=x1 i y=y1 realni brojevi takvi da je y'(x1,y1)=k1. Sada trebas pronaci neke x2,y2 razlicite od x1,y1 takve da je y'(x2,y2)=y'(x1,y1)=k1.[/quote]
A kako odmah znaš da postoje x1 i y1 td y'(x1,y1)=k1??
Frend i ja smo smislili nekakvo rješenje, da razdjelimo tu elipsu na 2 fcije, pa pokažemo da je derivacije svake surjekcija.
Samo nismo sigurni dal je to baš precizno...
I druga je ideja da uzmemo paralelan pravac kroz ishodište, on mora prolazit kroz elipsu, pa ono mora bit točka c između a i b sa svake strane koja ima koeficijent smjera jednak pravcu...
| Tomislav (napisa): | | Hint: Izrazi y'. Fiksiraj k=k1 i neka su sada x=x1 i y=y1 realni brojevi takvi da je y'(x1,y1)=k1. Sada trebas pronaci neke x2,y2 razlicite od x1,y1 takve da je y'(x2,y2)=y'(x1,y1)=k1. |
A kako odmah znaš da postoje x1 i y1 td y'(x1,y1)=k1??
Frend i ja smo smislili nekakvo rješenje, da razdjelimo tu elipsu na 2 fcije, pa pokažemo da je derivacije svake surjekcija.
Samo nismo sigurni dal je to baš precizno...
I druga je ideja da uzmemo paralelan pravac kroz ishodište, on mora prolazit kroz elipsu, pa ono mora bit točka c između a i b sa svake strane koja ima koeficijent smjera jednak pravcu...
|
|
| [Vrh] |
|
meda
Forumaš(ica)

Pridružen/a: 09. 01. 2010. (09:29:23)
Postovi: (A0)16
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 17:07 ned, 3. 4. 2011 Naslov: Postano: 17:07 ned, 3. 4. 2011 Naslov: |
    |
|
|
Da, i ja mislim da je potrebno pokazati da za svaki [latex]k \in \mathbb{R}[/latex] postoji takav uređeni par točaka (nakon što se pokaže, ako postoji neki, da ih ima barem dva).
Moja ideja je, nakon što se pokaže da ih ima barem dvije, da se izraz [latex]y'(x)[/latex] izrazi kao funkcija (po mogućnosti jedne varijable) i da se pokaže da je surjektivna. Ako se to pokaže, onda se zna da se svaki takav realni broj postiže.
Eto, ako bude trebalo, raspisat ću i svoje rješenje pa možete vidjeti ako je točno i ako zadovoljava vaše potrebe. :P
Da, i ja mislim da je potrebno pokazati da za svaki 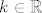 postoji takav uređeni par točaka (nakon što se pokaže, ako postoji neki, da ih ima barem dva). postoji takav uređeni par točaka (nakon što se pokaže, ako postoji neki, da ih ima barem dva).
Moja ideja je, nakon što se pokaže da ih ima barem dvije, da se izraz 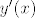 izrazi kao funkcija (po mogućnosti jedne varijable) i da se pokaže da je surjektivna. Ako se to pokaže, onda se zna da se svaki takav realni broj postiže. izrazi kao funkcija (po mogućnosti jedne varijable) i da se pokaže da je surjektivna. Ako se to pokaže, onda se zna da se svaki takav realni broj postiže.
Eto, ako bude trebalo, raspisat ću i svoje rješenje pa možete vidjeti ako je točno i ako zadovoljava vaše potrebe. 
|
|
| [Vrh] |
|
mrma
Forumaš(ica)

Pridružen/a: 15. 01. 2011. (12:28:40)
Postovi: (5)16
|
 Postano: 17:39 ned, 3. 4. 2011 Naslov: Postano: 17:39 ned, 3. 4. 2011 Naslov: |
    |
|
|
[quote="Phoenix"]Da, i ja mislim da je potrebno pokazati da za svaki [latex]k \in \mathbb{R}[/latex] postoji takav uređeni par točaka (nakon što se pokaže, ako postoji neki, da ih ima barem dva).
Moja ideja je, nakon što se pokaže da ih ima barem dvije, da se izraz [latex]y'(x)[/latex] izrazi kao funkcija (po mogućnosti jedne varijable) i da se pokaže da je surjektivna. Ako se to pokaže, onda se zna da se svaki takav realni broj postiže.
Eto, ako bude trebalo, raspisat ću i svoje rješenje pa možete vidjeti ako je točno i ako zadovoljava vaše potrebe. :P[/quote]
ajde ako ti se da, napisi svoje rjesenje
| Phoenix (napisa): | Da, i ja mislim da je potrebno pokazati da za svaki 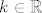 postoji takav uređeni par točaka (nakon što se pokaže, ako postoji neki, da ih ima barem dva). postoji takav uređeni par točaka (nakon što se pokaže, ako postoji neki, da ih ima barem dva).
Moja ideja je, nakon što se pokaže da ih ima barem dvije, da se izraz 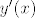 izrazi kao funkcija (po mogućnosti jedne varijable) i da se pokaže da je surjektivna. Ako se to pokaže, onda se zna da se svaki takav realni broj postiže. izrazi kao funkcija (po mogućnosti jedne varijable) i da se pokaže da je surjektivna. Ako se to pokaže, onda se zna da se svaki takav realni broj postiže.
Eto, ako bude trebalo, raspisat ću i svoje rješenje pa možete vidjeti ako je točno i ako zadovoljava vaše potrebe.  |
ajde ako ti se da, napisi svoje rjesenje
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 17:41 ned, 3. 4. 2011 Naslov: Postano: 17:41 ned, 3. 4. 2011 Naslov: |
    |
|
|
Dakle...
[latex]y'(x)=\frac{y-2x}{2y-x}[/latex]
Pretpostavimo da postoji uređeni par točaka za koji vrijedi [latex]y'(x)=k, k \in \mathbb{R}[/latex]. Zanima me je li to i jedini par točaka.
Stavimo: [latex]\frac{y_{1}-2x_{1}}{2y_{1}-x_{1}}=\frac{y_{2}-2x_{2}}{2y_{2}-x_{2}}[/latex]. (Zapravo hoću vidjeti mora li nužno iz ovoga vrijediti [latex]x_{1}=x_{2}[/latex] i [latex]y_{1}=y_{2}[/latex].)
Iz gornje jednadžbe dobivamo da mora vrijediti [latex]\frac{x_{1}}{y_{1}}=\frac{x_{2}}{y_{2}}[/latex]. Neka je onda taj razlomak jednak [latex]S[/latex]. Početnu relaciju ([latex]x^2-xy+y^2-1=0[/latex]) dijelimo s [latex]y^2[/latex] (naravno, uvrstimo [latex]x_{1}, y_{1}[/latex], odnosno [latex]x_{2}, y_{2}[/latex]). I dobivamo:
[latex]x= \pm \frac{1}{\sqrt{S^2-S+1}}[/latex].
To bi značilo da postoje dva uređena para točaka koji daju traženi omjer [latex]S[/latex], a taj omjer je jedinstveno određen zadanim koeficijentom [latex]k[/latex]. Stoga imamo dvije tražene točke.
Kako pokazati da takve točke postoje za svaki [latex]k \in \mathbb{R}[/latex]? Znamo da je [latex]y'(x)=\frac{y-2x}{2y-x}[/latex], [latex]y=xS[/latex] i [latex]x= \pm \frac{1}{\sqrt{S^2-S+1}}[/latex], a iz toga dobivamo:
[latex]y'=\frac{S-2}{2S-1}[/latex].
Ova funkcija je surjekcija na [latex]\mathbb{R} \backslash \left\{ \frac{1}{2} \right\}[/latex]. A za [latex]k = y' = \frac{1}{2}[/latex] ćemo ovako pokazati (deriviramo početnu relaciju):
[latex]2x-y-xy'+2yy'=0[/latex]
[latex]2x-y-\frac{x}{2}+y=0[/latex]
[latex]x=0[/latex]
To uvrstimo u početnu relaciju i dobivamo [latex]y = \pm 1[/latex]. To znači da i za [latex]k=\frac{1}{2}[/latex] imamo tražene točke.
Evo, ovako to izgleda natipkano (opet) na brzinu. Nadam se da nema grešaka - provjerite sami (u smislu postupka, ne tipfelera). :oops:
Dakle...
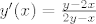
Pretpostavimo da postoji uređeni par točaka za koji vrijedi 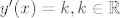 . Zanima me je li to i jedini par točaka. . Zanima me je li to i jedini par točaka.
Stavimo: 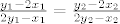 . (Zapravo hoću vidjeti mora li nužno iz ovoga vrijediti . (Zapravo hoću vidjeti mora li nužno iz ovoga vrijediti 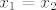 i i 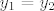 .) .)
Iz gornje jednadžbe dobivamo da mora vrijediti 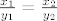 . Neka je onda taj razlomak jednak . Neka je onda taj razlomak jednak  . Početnu relaciju ( . Početnu relaciju (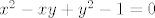 ) dijelimo s ) dijelimo s 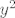 (naravno, uvrstimo (naravno, uvrstimo 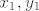 , odnosno , odnosno 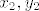 ). I dobivamo: ). I dobivamo:
 . .
To bi značilo da postoje dva uređena para točaka koji daju traženi omjer  , a taj omjer je jedinstveno određen zadanim koeficijentom , a taj omjer je jedinstveno određen zadanim koeficijentom  . Stoga imamo dvije tražene točke. . Stoga imamo dvije tražene točke.
Kako pokazati da takve točke postoje za svaki 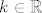 ? Znamo da je ? Znamo da je 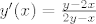 , , 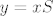 i i  , a iz toga dobivamo: , a iz toga dobivamo:
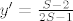 . .
Ova funkcija je surjekcija na 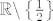 . A za . A za 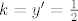 ćemo ovako pokazati (deriviramo početnu relaciju): ćemo ovako pokazati (deriviramo početnu relaciju):
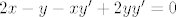
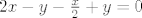

To uvrstimo u početnu relaciju i dobivamo 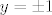 . To znači da i za . To znači da i za 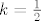 imamo tražene točke. imamo tražene točke.
Evo, ovako to izgleda natipkano (opet) na brzinu. Nadam se da nema grešaka - provjerite sami (u smislu postupka, ne tipfelera). 
Zadnja promjena: Phoenix; 17:42 ned, 3. 4. 2011; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
mrma
Forumaš(ica)

Pridružen/a: 15. 01. 2011. (12:28:40)
Postovi: (5)16
|
 Postano: 21:06 ned, 3. 4. 2011 Naslov: Postano: 21:06 ned, 3. 4. 2011 Naslov: |
    |
|
|
[quote="Phoenix"]Dakle...
[latex]y'(x)=\frac{y-2x}{2y-x}[/latex]
Pretpostavimo da postoji uređeni par točaka za koji vrijedi [latex]y'(x)=k, k \in \mathbb{R}[/latex]. Zanima me je li to i jedini par točaka.
Stavimo: [latex]\frac{y_{1}-2x_{1}}{2y_{1}-x_{1}}=\frac{y_{2}-2x_{2}}{2y_{2}-x_{2}}[/latex]. (Zapravo hoću vidjeti mora li nužno iz ovoga vrijediti [latex]x_{1}=x_{2}[/latex] i [latex]y_{1}=y_{2}[/latex].)
Iz gornje jednadžbe dobivamo da mora vrijediti [latex]\frac{x_{1}}{y_{1}}=\frac{x_{2}}{y_{2}}[/latex]. Neka je onda taj razlomak jednak [latex]S[/latex]. Početnu relaciju ([latex]x^2-xy+y^2-1=0[/latex]) dijelimo s [latex]y^2[/latex] (naravno, uvrstimo [latex]x_{1}, y_{1}[/latex], odnosno [latex]x_{2}, y_{2}[/latex]). I dobivamo:
[latex]x= \pm \frac{1}{\sqrt{S^2-S+1}}[/latex].
To bi značilo da postoje dva uređena para točaka koji daju traženi omjer [latex]S[/latex], a taj omjer je jedinstveno određen zadanim koeficijentom [latex]k[/latex]. Stoga imamo dvije tražene točke.
Kako pokazati da takve točke postoje za svaki [latex]k \in \mathbb{R}[/latex]? Znamo da je [latex]y'(x)=\frac{y-2x}{2y-x}[/latex], [latex]y=xS[/latex] i [latex]x= \pm \frac{1}{\sqrt{S^2-S+1}}[/latex], a iz toga dobivamo:
[latex]y'=\frac{S-2}{2S-1}[/latex].
Ova funkcija je surjekcija na [latex]\mathbb{R} \backslash \left\{ \frac{1}{2} \right\}[/latex]. A za [latex]k = y' = \frac{1}{2}[/latex] ćemo ovako pokazati (deriviramo početnu relaciju):
[latex]2x-y-xy'+2yy'=0[/latex]
[latex]2x-y-\frac{x}{2}+y=0[/latex]
[latex]x=0[/latex]
To uvrstimo u početnu relaciju i dobivamo [latex]y = \pm 1[/latex]. To znači da i za [latex]k=\frac{1}{2}[/latex] imamo tražene točke.
Evo, ovako to izgleda natipkano (opet) na brzinu. Nadam se da nema grešaka - provjerite sami (u smislu postupka, ne tipfelera). :oops:[/quote]
hvala!
| Phoenix (napisa): | Dakle...
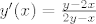
Pretpostavimo da postoji uređeni par točaka za koji vrijedi 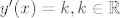 . Zanima me je li to i jedini par točaka. . Zanima me je li to i jedini par točaka.
Stavimo: 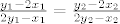 . (Zapravo hoću vidjeti mora li nužno iz ovoga vrijediti . (Zapravo hoću vidjeti mora li nužno iz ovoga vrijediti 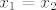 i i 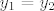 .) .)
Iz gornje jednadžbe dobivamo da mora vrijediti 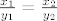 . Neka je onda taj razlomak jednak . Neka je onda taj razlomak jednak  . Početnu relaciju ( . Početnu relaciju (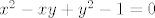 ) dijelimo s ) dijelimo s 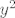 (naravno, uvrstimo (naravno, uvrstimo 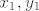 , odnosno , odnosno 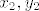 ). I dobivamo: ). I dobivamo:
 . .
To bi značilo da postoje dva uređena para točaka koji daju traženi omjer  , a taj omjer je jedinstveno određen zadanim koeficijentom , a taj omjer je jedinstveno određen zadanim koeficijentom  . Stoga imamo dvije tražene točke. . Stoga imamo dvije tražene točke.
Kako pokazati da takve točke postoje za svaki 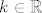 ? Znamo da je ? Znamo da je 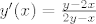 , , 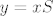 i i  , a iz toga dobivamo: , a iz toga dobivamo:
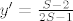 . .
Ova funkcija je surjekcija na 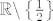 . A za . A za 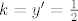 ćemo ovako pokazati (deriviramo početnu relaciju): ćemo ovako pokazati (deriviramo početnu relaciju):
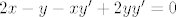
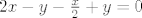

To uvrstimo u početnu relaciju i dobivamo 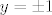 . To znači da i za . To znači da i za 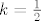 imamo tražene točke. imamo tražene točke.
Evo, ovako to izgleda natipkano (opet) na brzinu. Nadam se da nema grešaka - provjerite sami (u smislu postupka, ne tipfelera).  |
hvala!
|
|
| [Vrh] |
|
|








