| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
psujetic
Forumaš(ica)
Pridružen/a: 27. 04. 2007. (21:11:30)
Postovi: (13)16
|
|
| [Vrh] |
|
tinky
Forumaš(ica)
Pridružen/a: 20. 06. 2008. (11:59:08)
Postovi: (3F)16
|
|
| [Vrh] |
|
palcica
Forumaš(ica)

Pridružen/a: 13. 06. 2010. (16:01:19)
Postovi: (10)16
|
|
| [Vrh] |
|
palcica
Forumaš(ica)

Pridružen/a: 13. 06. 2010. (16:01:19)
Postovi: (10)16
|
|
| [Vrh] |
|
mycky1111
Forumaš(ica)

Pridružen/a: 26. 05. 2008. (11:59:07)
Postovi: (D4)16
Spol: 
|
 Postano: 19:55 ned, 3. 4. 2011 Naslov: Postano: 19:55 ned, 3. 4. 2011 Naslov: |
    |
|
|
zadnje sto smo radili je 1.50
cak nismo radili ni osnovni Cantorov teorem, al ja bi ga procitala, za svaki slucaj
nego, onaj zadnji zadatak iz kolokvija, supermum nesto, mi to nismo jos radili na vjezbama, jel?
zadnje sto smo radili je 1.50
cak nismo radili ni osnovni Cantorov teorem, al ja bi ga procitala, za svaki slucaj
nego, onaj zadnji zadatak iz kolokvija, supermum nesto, mi to nismo jos radili na vjezbama, jel?
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 12:56 pon, 4. 4. 2011 Naslov: Postano: 12:56 pon, 4. 4. 2011 Naslov: |
    |
|
|
[quote=".anchy."]a kako bi išli 5. i 7.? evo najdužeg linka kojeg sam ikad vidjela :D[/quote]
onda malo proguglaš i dobiješ ovakav linkić http://urlm.in/hlmw :)
a što se zadataka tiče, peti nisam točno siguran kako ide, moram pogledat još malo relacije. Sedmi definiraš funkciju koja funkciji sa [0,1] u <0, +infty> pridružuje njeno neprekidno proširenje oko točke -101. znaš da funkcija sa [0,1] u <0,+infty> ima 2 na c, a ovo što napraviš je injekcija u neprekidne funkcije u točki -101. također, znaš da njih ne može biti više od 2 na c, jer svih funkcija definiranih sa R u R ima 2 na c. Mislim d aje to to, samo trebaš malo formalno raspisat, al i za ovakvo nekakvo objašnjenje mislim da daju barem pola bodova
| .anchy. (napisa): | a kako bi išli 5. i 7.? evo najdužeg linka kojeg sam ikad vidjela  |
onda malo proguglaš i dobiješ ovakav linkić http://urlm.in/hlmw 
a što se zadataka tiče, peti nisam točno siguran kako ide, moram pogledat još malo relacije. Sedmi definiraš funkciju koja funkciji sa [0,1] u <0, +infty> pridružuje njeno neprekidno proširenje oko točke -101. znaš da funkcija sa [0,1] u <0,+infty> ima 2 na c, a ovo što napraviš je injekcija u neprekidne funkcije u točki -101. također, znaš da njih ne može biti više od 2 na c, jer svih funkcija definiranih sa R u R ima 2 na c. Mislim d aje to to, samo trebaš malo formalno raspisat, al i za ovakvo nekakvo objašnjenje mislim da daju barem pola bodova
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
 Postano: 13:38 pon, 4. 4. 2011 Naslov: Postano: 13:38 pon, 4. 4. 2011 Naslov: |
    |
|
|
5. bi išao nekako ovako:
[latex]R = \{(x,\rho(x)) | \rho \hspace{1mm}je \hspace{1mm}funkcija\}[/latex]
to znači da će za svaki x postojati jedinstveni element u relaciji oblika:
[latex](x,\rho(x))[/latex]
jer kada bi postojala 2 različita sa istim prvim elementom, onda [latex]\rho[/latex] ne bi bila funkcija.
[latex]R^{-1} = \{(\rho(x), x) | (x,\rho(x)) \in R \}[/latex]
to znači da će u kompoziciji ove dvije biti samo oni oblika
[latex](\rho(x),\rho(x))[/latex]
( to malo raspisati sa onom definicijom kompozijcije ) i to zato što je [latex]\rho[/latex] funkcija.
S obzirom da je [latex]\rho[/latex] funkcija sa A u A, onda je i [latex]\rho(x) \in A[/latex] tj.
[latex](\rho(x),\rho(x)) \subseteq I_{A} \hspace{1mm}\forall \rho(x)[/latex]
tj.
[latex]R\circ R^{-1} \subseteq I_{A}[/latex]
5. bi išao nekako ovako:

to znači da će za svaki x postojati jedinstveni element u relaciji oblika:
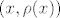
jer kada bi postojala 2 različita sa istim prvim elementom, onda 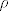 ne bi bila funkcija. ne bi bila funkcija.
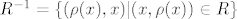
to znači da će u kompoziciji ove dvije biti samo oni oblika

( to malo raspisati sa onom definicijom kompozijcije ) i to zato što je 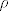 funkcija. funkcija.
S obzirom da je 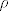 funkcija sa A u A, onda je i funkcija sa A u A, onda je i 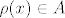 tj. tj.
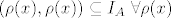
tj.

|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 14:33 pon, 4. 4. 2011 Naslov: Postano: 14:33 pon, 4. 4. 2011 Naslov: |
    |
|
|
uzmi funkciju koja nizu a_n pridružuje niz a_1, -1, 1, a_2, -2, 2, a_3, -3, 3, ... i to je injekcija sa skupa nizova na skup surjektivnih nizova. nizova ima c, kardinalnost nizova je onda manja od kardinalnosti surjektivnih nizova, pa je kardinalnost surjektivnih nizova veća il jednaka c-u.
ustvari, nisam siguran baš da je voo injekcija, ustvari, da, je je, injekcija. nije bitno gledati elemente niza koje dobiješ, neg je bitno gledati čitav niz, jer funkcija barata sa nizovima, a boli ju uvo za elemente niza.
Znači, ako imaš dva niza koji se razlikuju, neka su to a_n, b_n, neka se razlikuju na indeksu m, onda se i nizovi f(a_n) i f(b_n) razlikuju, sada na mjestu 3*m -2.
to je to, još samo treba zapisati djelovanje ove funkcije
f(a_n)_m = a_n , m = 3*n-2, -n , m=3*n-1, n, m = 3*n
[size=9][color=#999999]Added after 37 seconds:[/color][/size]
znači f(a_n) je niz, pa gledam njegove elemente na mjestu m, daklem f(a_n)_m
uzmi funkciju koja nizu a_n pridružuje niz a_1, -1, 1, a_2, -2, 2, a_3, -3, 3, ... i to je injekcija sa skupa nizova na skup surjektivnih nizova. nizova ima c, kardinalnost nizova je onda manja od kardinalnosti surjektivnih nizova, pa je kardinalnost surjektivnih nizova veća il jednaka c-u.
ustvari, nisam siguran baš da je voo injekcija, ustvari, da, je je, injekcija. nije bitno gledati elemente niza koje dobiješ, neg je bitno gledati čitav niz, jer funkcija barata sa nizovima, a boli ju uvo za elemente niza.
Znači, ako imaš dva niza koji se razlikuju, neka su to a_n, b_n, neka se razlikuju na indeksu m, onda se i nizovi f(a_n) i f(b_n) razlikuju, sada na mjestu 3*m -2.
to je to, još samo treba zapisati djelovanje ove funkcije
f(a_n)_m = a_n , m = 3*n-2, -n , m=3*n-1, n, m = 3*n
Added after 37 seconds:
znači f(a_n) je niz, pa gledam njegove elemente na mjestu m, daklem f(a_n)_m
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
(s)Venn
Forumaš(ica)

Pridružen/a: 18. 02. 2009. (17:59:25)
Postovi: (40)16
Lokacija: Velika Gorica
|
 Postano: 14:38 pon, 4. 4. 2011 Naslov: Postano: 14:38 pon, 4. 4. 2011 Naslov: |
    |
|
|
@.anchy.
Vjerujem da je ovako: označimo sa S skup svih surjektivnih nizova u Z. U obratnom smjeru konstruiraš injekciju f:{svi nizovi u Z}->S na način:
f(an) = (a0, 0, a1, 1, a2, -1, a3, 2, a4, -2, ... )
@.anchy.
Vjerujem da je ovako: označimo sa S skup svih surjektivnih nizova u Z. U obratnom smjeru konstruiraš injekciju f:{svi nizovi u Z}->S na način:
f(an) = (a0, 0, a1, 1, a2, -1, a3, 2, a4, -2, ... )
_________________ ..pišem pjesme, sviram bluz, radost i tugu na stihove lomim.. |
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
 Postano: 14:46 pon, 4. 4. 2011 Naslov: Postano: 14:46 pon, 4. 4. 2011 Naslov: |
    |
|
|
[quote=".anchy."]a zadatak iz skripte 68(skup svih surjektivnih nizova cijelih brojeva)? jasno mi je da ih ima manje od c, ali kako dokazati obratnu nejednakost?[/quote]
sličan smo radili na vježbama. Neka je S skup svih surjektivnih nizova cijelih brojeva. lagano se pokaže da je k( S ) <= c. ( tj. to je podskup od svih svih nizova cijelih brojeva kojih ima c ).
znači želimo napraviti injekciju sa nekog skupa veličine c na S.
uzmimo da je K skup svih nizova prirodnih brojeva. kardinalnost od K je c.
što ćemo u biti raditi: nizove prirodnih brojeva želimo preslikati u surjektivne nizove cijelih brojeva.
pa ako imamo niz prirodnih brojeva: ( a_0, a_1, a_2, a_3, ... )
mi ga preslikamo u : ( a_0, 0, a_1, 1, a_2, -1, a_3, 2, a_4, -2,... )
i dobili smo surjektivan niz cijelih brojeva. funkcija je očito injekcija jer će različiti nizovi prirodnih brojeva imati najmanje jedan različiti član, pa će i nizovi koje smo dobili iz različitih nizova imati najmanje jedan različiti član.
ima i formula za funkciju: ( a je niz )
[f(a)](n) = a_(n/2), ako je n paran
n+1/4, ako je n%4 = 3.
-(n-1)/4, ako je n%4 = 1
s time da je [f(a)](1) = 0.
S obzirom da je f:K->S injekcija to znači da je k(S) >= k( K ) = c.
Zadaci kao 8. iz prošle godine neće bit na kolokviju?
| .anchy. (napisa): | | a zadatak iz skripte 68(skup svih surjektivnih nizova cijelih brojeva)? jasno mi je da ih ima manje od c, ali kako dokazati obratnu nejednakost? |
sličan smo radili na vježbama. Neka je S skup svih surjektivnih nizova cijelih brojeva. lagano se pokaže da je k( S ) ⇐ c. ( tj. to je podskup od svih svih nizova cijelih brojeva kojih ima c ).
znači želimo napraviti injekciju sa nekog skupa veličine c na S.
uzmimo da je K skup svih nizova prirodnih brojeva. kardinalnost od K je c.
što ćemo u biti raditi: nizove prirodnih brojeva želimo preslikati u surjektivne nizove cijelih brojeva.
pa ako imamo niz prirodnih brojeva: ( a_0, a_1, a_2, a_3, ... )
mi ga preslikamo u : ( a_0, 0, a_1, 1, a_2, -1, a_3, 2, a_4, -2,... )
i dobili smo surjektivan niz cijelih brojeva. funkcija je očito injekcija jer će različiti nizovi prirodnih brojeva imati najmanje jedan različiti član, pa će i nizovi koje smo dobili iz različitih nizova imati najmanje jedan različiti član.
ima i formula za funkciju: ( a je niz )
[f(a)](n) = a_(n/2), ako je n paran
n+1/4, ako je n%4 = 3.
-(n-1)/4, ako je n%4 = 1
s time da je [f(a)](1) = 0.
S obzirom da je f:K→S injekcija to znači da je k(S) >= k( K ) = c.
Zadaci kao 8. iz prošle godine neće bit na kolokviju?
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 15:05 pon, 4. 4. 2011 Naslov: Postano: 15:05 pon, 4. 4. 2011 Naslov: |
    |
|
|
da da, ja sam zaboravio nulicu dodat :$
da, osmi zadatak pokriva gradivo idućeg poglavlja i ne dolazi u kolokvij
da da, ja sam zaboravio nulicu dodat :$
da, osmi zadatak pokriva gradivo idućeg poglavlja i ne dolazi u kolokvij
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 18:29 pon, 4. 4. 2011 Naslov: Postano: 18:29 pon, 4. 4. 2011 Naslov: |
    |
|
|
Još jedna zamolba: bi li netko mogao objasniti rješenje zad 97 u skripti?
nije mi jasna unija f-ja,što to znači, i je li mi f:<-oo,0>-->R?
i kako znam kod tih zadataka s funkcijama koju ću domenu uzeti-funkcije s čega u kaj?
i bi li rješenje zadatka 98 bilo dobro kao rješenje 97.zadatka?
i,što u rj.96. znači <-oo, R>?
Još jedna zamolba: bi li netko mogao objasniti rješenje zad 97 u skripti?
nije mi jasna unija f-ja,što to znači, i je li mi f:<-oo,0>-->R?
i kako znam kod tih zadataka s funkcijama koju ću domenu uzeti-funkcije s čega u kaj?
i bi li rješenje zadatka 98 bilo dobro kao rješenje 97.zadatka?
i,što u rj.96. znači <-oo, R>?
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 20:19 pon, 4. 4. 2011 Naslov: Postano: 20:19 pon, 4. 4. 2011 Naslov: |
    |
|
|
[quote=".anchy."]Još jedna zamolba: bi li netko mogao objasniti rješenje zad 97 u skripti?
nije mi jasna unija f-ja,što to znači, i je li mi f:<-oo,0>-->R?[/quote]
njaha, sad mi je jasno. F uzima funkcije koje su definirane na <-infty, 0>, i poprimaju vrijednosti u R. Na negativnim x-evima je F(f)(x) = f(x), a na nenegativnim je F(f)(x)=sin(x), tu je opet očito da će sinus opalit svaku točku iz [0,1], pa će te funkcije zadovoljavati dani uvjet. Ovu uniju su mogli zapisati i jednostavno kao +, al kako je svaka funkcija relacija, to je, onda, valjda ekvivalentno
[quote]
i kako znam kod tih zadataka s funkcijama koju ću domenu uzeti-funkcije s čega u kaj?[/quote]
reko bih da nema nekog pravila posebnog. moraš paziti da dobro definiraš funkcije kako nebi došlo do problema sa domenama, sa svojstvima skupa čiju kardinalnost tražiš, i tako to
[quote]
i bi li rješenje zadatka 98 bilo dobro kao rješenje 97.zadatka?
[/quote]
nebi, barem ne ovako definirati F kako je u 97., jer funkcije moraju biti ograničene, pa onda tome doskače sa ovim funkcijama što primaju vrijednost u <0,1>, a van <0,1>, što im je i domena, definira ju kao nulu (btw mogao je staviti i 7 komotno, ili bilo koji broj, isti jarac)
[quote]
i,što u rj.96. znači <-oo, R>?[/quote]
tipfeler. treba pisati 0 na oba mjesta
| .anchy. (napisa): | Još jedna zamolba: bi li netko mogao objasniti rješenje zad 97 u skripti?
nije mi jasna unija f-ja,što to znači, i je li mi f:←oo,0>→R? |
njaha, sad mi je jasno. F uzima funkcije koje su definirane na ←infty, 0>, i poprimaju vrijednosti u R. Na negativnim x-evima je F(f)(x) = f(x), a na nenegativnim je F(f)(x)=sin(x), tu je opet očito da će sinus opalit svaku točku iz [0,1], pa će te funkcije zadovoljavati dani uvjet. Ovu uniju su mogli zapisati i jednostavno kao +, al kako je svaka funkcija relacija, to je, onda, valjda ekvivalentno
| Citat: |
i kako znam kod tih zadataka s funkcijama koju ću domenu uzeti-funkcije s čega u kaj? |
reko bih da nema nekog pravila posebnog. moraš paziti da dobro definiraš funkcije kako nebi došlo do problema sa domenama, sa svojstvima skupa čiju kardinalnost tražiš, i tako to
| Citat: |
i bi li rješenje zadatka 98 bilo dobro kao rješenje 97.zadatka?
|
nebi, barem ne ovako definirati F kako je u 97., jer funkcije moraju biti ograničene, pa onda tome doskače sa ovim funkcijama što primaju vrijednost u <0,1>, a van <0,1>, što im je i domena, definira ju kao nulu (btw mogao je staviti i 7 komotno, ili bilo koji broj, isti jarac)
| Citat: |
i,što u rj.96. znači ←oo, R>? |
tipfeler. treba pisati 0 na oba mjesta
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
tomitza
Forumaš(ica)


Pridružen/a: 28. 11. 2008. (19:50:48)
Postovi: (58)16
|
|
| [Vrh] |
|
bozidarsevo
Forumaš(ica)


Pridružen/a: 17. 09. 2008. (10:15:01)
Postovi: (1D1)16
Spol: 
Lokacija: Samobor
|
|
| [Vrh] |
|
|














