|
Very simple. :D
Prvo: [latex]m := 2006^{2006}[/latex] je ocito paran broj. To znaci da suma prvih [i]m[/i] prostih brojeva sadrzi [i]m[/i]-1 neparan broj (jer je samo 2 paran).
Drugo: suma neparno mnogo neparnih brojeva je neparan broj. Dodamo tome onu dvojku, ostaje neparan broj.
Dakle, M je neparan, tj. [latex]M = 2k+1[/latex] za neki cijeli [i]k[/i]. Nas zanima ostatak pri dijeljenju [latex]M^2[/latex] s 8.
[latex]M^2 = (2k+1)^2 = 4k^2 + 4k + 1 = 4k(k+1)+1[/latex]
Primijeti da je [latex]k(k+1)[/latex] umnozak dva uzastopna cijela broja, pa je taj umnozak paran (jer je jedan od te dvojice paran), sto znaci da je [latex]4k(k+1)[/latex] djeljiv s 8, pa je ostatak pri dijeljenju [latex]M^2[/latex] s 8 jednak 1. 8)
Very simple. 
Prvo: 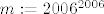 je ocito paran broj. To znaci da suma prvih m prostih brojeva sadrzi m-1 neparan broj (jer je samo 2 paran). je ocito paran broj. To znaci da suma prvih m prostih brojeva sadrzi m-1 neparan broj (jer je samo 2 paran).
Drugo: suma neparno mnogo neparnih brojeva je neparan broj. Dodamo tome onu dvojku, ostaje neparan broj.
Dakle, M je neparan, tj. 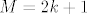 za neki cijeli k. Nas zanima ostatak pri dijeljenju za neki cijeli k. Nas zanima ostatak pri dijeljenju 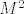 s 8. s 8.
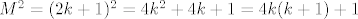
Primijeti da je 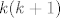 umnozak dva uzastopna cijela broja, pa je taj umnozak paran (jer je jedan od te dvojice paran), sto znaci da je umnozak dva uzastopna cijela broja, pa je taj umnozak paran (jer je jedan od te dvojice paran), sto znaci da je 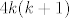 djeljiv s 8, pa je ostatak pri dijeljenju djeljiv s 8, pa je ostatak pri dijeljenju 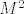 s 8 jednak 1. s 8 jednak 1. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |




