| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 20:33 uto, 19. 4. 2011 Naslov: Teorijsko pitanje Postano: 20:33 uto, 19. 4. 2011 Naslov: Teorijsko pitanje |
    |
|
|
Prolazim malo kroz skriptu profesora Guljaša, i došao sam do dijela gdje pokazuje [latex](e^x)' = e^x[/latex]. ( http://web.math.hr/~guljas/skripte/MATANALuR.pdf , na 96toj stranici).
E sad, kao što vidite ako ste otvorili ovaj link i odskrolali na 96tu stranicu, taj dokaz zauzima otprilike jednu stranicu, no mene muči - nije li se to moglo argumentirati ovako:
[latex](e^c)' = lim_{x\rightarrow c} \frac{e^x - e^c}{x - c}[/latex], pa ako uvedem supstituciju [latex]t = x - c[/latex] onda imam:
[latex]lim_{t\rightarrow 0} \frac{e^{t+c} - e^c}{t} = e^c \cdot lim_{t\rightarrow 0}(\frac{e^t - 1}{t}) = e^c [/latex]
E sad, pošto nisam stavljao nikakve uvjete na c, a eksponencijalna f-ja je lijepo definirana i neprekidna na čitavom R mogu zaključiti da je [latex](e^c)' = e^c, \forall c \epsilon R[/latex], pa tako i da je [latex](e^x)' = e^x[/latex].
Gdje je rupa u ovakvoj logici, jer sumnjam da bi se u skripti to išlo bezveze komplicirati?
Prolazim malo kroz skriptu profesora Guljaša, i došao sam do dijela gdje pokazuje 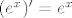 . ( http://web.math.hr/~guljas/skripte/MATANALuR.pdf , na 96toj stranici). . ( http://web.math.hr/~guljas/skripte/MATANALuR.pdf , na 96toj stranici).
E sad, kao što vidite ako ste otvorili ovaj link i odskrolali na 96tu stranicu, taj dokaz zauzima otprilike jednu stranicu, no mene muči - nije li se to moglo argumentirati ovako:
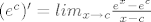 , pa ako uvedem supstituciju , pa ako uvedem supstituciju 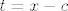 onda imam: onda imam:
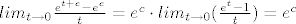
E sad, pošto nisam stavljao nikakve uvjete na c, a eksponencijalna f-ja je lijepo definirana i neprekidna na čitavom R mogu zaključiti da je 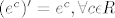 , pa tako i da je , pa tako i da je 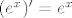 . .
Gdje je rupa u ovakvoj logici, jer sumnjam da bi se u skripti to išlo bezveze komplicirati?
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 0:22 sri, 20. 4. 2011 Naslov: Re: Teorijsko pitanje Postano: 0:22 sri, 20. 4. 2011 Naslov: Re: Teorijsko pitanje |
    |
|
|
[quote="ceps"]E sad, kao što vidite ako ste otvorili ovaj link i odskrolali na 96tu stranicu, taj dokaz zauzima otprilike jednu stranicu, no mene muči - nije li se to moglo argumentirati ovako:
[latex](e^c)' = lim_{x\rightarrow c} \frac{e^x - e^c}{x - c}[/latex], pa ako uvedem supstituciju [latex]t = x - c[/latex] onda imam:
[latex]lim_{t\rightarrow 0} \frac{e^{t+c} - e^c}{t} = e^c \cdot lim_{t\rightarrow 0}(\frac{e^t - 1}{t}) = e^c [/latex]
E sad, pošto nisam stavljao nikakve uvjete na c, a eksponencijalna f-ja je lijepo definirana i neprekidna na čitavom R mogu zaključiti da je [latex](e^c)' = e^c, \forall c \epsilon R[/latex], pa tako i da je [latex](e^x)' = e^x[/latex].
Gdje je rupa u ovakvoj logici, jer sumnjam da bi se u skripti to išlo bezveze komplicirati?[/quote]
Problem kod eksponencijalne funkcije na prvoj godini je taj što je jako teško definirati na [latex]\mathbb{R}[/latex]. U tvom dokazu još trebaš pokazati da je [latex]\lim_{t\rightarrow 0}(\frac{e^t - 1}{t})=1 [/latex]. Kako ćeš to?
| ceps (napisa): | E sad, kao što vidite ako ste otvorili ovaj link i odskrolali na 96tu stranicu, taj dokaz zauzima otprilike jednu stranicu, no mene muči - nije li se to moglo argumentirati ovako:
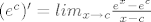 , pa ako uvedem supstituciju , pa ako uvedem supstituciju 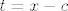 onda imam: onda imam:
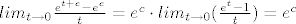
E sad, pošto nisam stavljao nikakve uvjete na c, a eksponencijalna f-ja je lijepo definirana i neprekidna na čitavom R mogu zaključiti da je 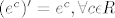 , pa tako i da je , pa tako i da je 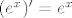 . .
Gdje je rupa u ovakvoj logici, jer sumnjam da bi se u skripti to išlo bezveze komplicirati? |
Problem kod eksponencijalne funkcije na prvoj godini je taj što je jako teško definirati na  . U tvom dokazu još trebaš pokazati da je . U tvom dokazu još trebaš pokazati da je 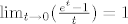 . Kako ćeš to? . Kako ćeš to?
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 0:27 sri, 20. 4. 2011 Naslov: Postano: 0:27 sri, 20. 4. 2011 Naslov: |
    |
|
|
@rafaelm, pa mislio sam da to ne treba dodatno objašnjavat, to je pokazano još davno u prvom semestru :) (str. 64 u skripti)
To je čak i jedna od onih formula sa službenog šalabahtera.
Nisam to posebno naglašavao, jer kako bi to izgledalo da se u svakom dokazu ponovno dokazuju sve leme, korolarčići i teoremi koji se koriste u tom dokazu...
@Tomislav, shvaćam ja što je profesor koristio i što ja koristim, ali me zanima ima li kakvih praktičnih razloga zašto je način u skripti bolji.
@rafaelm, pa mislio sam da to ne treba dodatno objašnjavat, to je pokazano još davno u prvom semestru  (str. 64 u skripti) (str. 64 u skripti)
To je čak i jedna od onih formula sa službenog šalabahtera.
Nisam to posebno naglašavao, jer kako bi to izgledalo da se u svakom dokazu ponovno dokazuju sve leme, korolarčići i teoremi koji se koriste u tom dokazu...
@Tomislav, shvaćam ja što je profesor koristio i što ja koristim, ali me zanima ima li kakvih praktičnih razloga zašto je način u skripti bolji.
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
|
| [Vrh] |
|
hstojanovic
Forumaš(ica)
Pridružen/a: 16. 10. 2010. (18:00:01)
Postovi: (30)16
Spol: 
|
|
| [Vrh] |
|
|










