| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
spam
Forumaš(ica)

Pridružen/a: 17. 05. 2011. (14:27:28)
Postovi: (2)16
Spol: 
|
|
| [Vrh] |
|
A_je_to
Forumaš(ica)

Pridružen/a: 19. 02. 2009. (16:51:22)
Postovi: (6D)16
Spol: 
|
|
| [Vrh] |
|
Togepi
Forumaš(ica)
Pridružen/a: 21. 11. 2010. (14:31:41)
Postovi: (2B)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 7:09 sri, 18. 5. 2011 Naslov: Postano: 7:09 sri, 18. 5. 2011 Naslov: |
    |
|
|
Što se tiče 2.8. a), radi se o običnoj integralnoj sumi funkcije [latex]f(x)=x[/latex] na segmentu [latex][0,2][/latex], do na jednu začkoljicu: dodaj na početku u sumu [latex]\displaystyle\frac{2n}{n^2}[/latex] (treba nam za vrijednost koja pripada zadnjem intervalu u subdiviziji). To ide u [latex]0[/latex], pa nikako ne mijenja postojanje niti sumu limesa.
E, sad izluči [latex]1/n[/latex], kako se to već uobičajeno radi, i imaš [latex]\displaystyle\frac{1}{n}(\frac{1}{n}+\frac{2}{n}+\ldots+\frac{2n-1}{n}+\frac{2n}{n})[/latex].
Primjećuješ da sad imaš običnu integralnu sumu. (Ako je tu neki problem, pitaj... :)) Dakle, traženi je limes [latex]\displaystyle\int_{0}^{2}xdx[/latex], a to je negdje [latex]1[/latex]. :)
Što se tiče 2.41. a), razuman hint mi se čini da izlučiš [latex]x[/latex] iz donjeg korijena, a nakon toga izvedeš supstituciju [latex]t=1/x[/latex], u kojem trenutku dobivaš da želiš integrirati [latex]\displaystyle\frac{-t^5}{\sqrt{1-t^2}}[/latex]. Sad trigonometrija ima smisla, ne? :)
Što se tiče 2.89., malo je teško objasniti bez crteža, ali ja bih išao ovako. Pretpostavljam da radimo samo s "desnom kružnicom" ([latex]3\cos\varphi[/latex] napravi dvije kružnice za [latex]\varphi\in[0,2\pi][/latex]). Ako ne, slična, tj. potpuno ista, stvar se može napraviti za lijevu kružnicu.
Okej, zanima nas samo površina iznad [latex]x[/latex]-osi. (Površina s druge strane je ista, pa samo množimo s [latex]2[/latex].)
E, sad, odredimo gdje se sijeku kružnica i kardioida. (Samo treba riješiti [latex]1+\cos(x)=3\cos(x)[/latex]). Ispada da to rade u [latex](r,\varphi)=(1/2,\pi/3)[/latex].
Sad, izračunaj površinu kardioide za [latex]\varphi\in[0,\pi/3][/latex]. Za to imaš formulu. Preostaje još dodati onaj mali dio kružnice "lijevo" od kardioide. No, to nam nije teško. Znamo da je to zapravo šestina površine kružnice umanjena za površinu trokuta kojeg omeđuju ishodište, središte kružnice (što je [latex](x,y)=(1.5,0)[/latex]) i točka [latex](r,\varphi)=(1/2,\pi/3)[/latex]. Radi se o jednakostraničnom trokutu, pa je njegovu površinu još posebno lako izračunati.
E, tako, sad sve to oduzmeš, zbrojiš i sl. i gotovi smo. :) Nisam tu baš puno objašnjavao, možda sam negdje i pogriješio, možda treba malo razmisliti (zašto je to jednakostranični trokut, zašto je ono šestina površine kružnice itd.), ali nadam se da je ovo korektan, dapače, solidan hint. :)
Što se tiče 2.8. a), radi se o običnoj integralnoj sumi funkcije 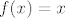 na segmentu na segmentu 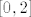 , do na jednu začkoljicu: dodaj na početku u sumu , do na jednu začkoljicu: dodaj na početku u sumu 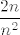 (treba nam za vrijednost koja pripada zadnjem intervalu u subdiviziji). To ide u (treba nam za vrijednost koja pripada zadnjem intervalu u subdiviziji). To ide u  , pa nikako ne mijenja postojanje niti sumu limesa. , pa nikako ne mijenja postojanje niti sumu limesa.
E, sad izluči 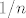 , kako se to već uobičajeno radi, i imaš , kako se to već uobičajeno radi, i imaš 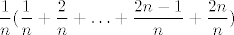 . .
Primjećuješ da sad imaš običnu integralnu sumu. (Ako je tu neki problem, pitaj...  ) Dakle, traženi je limes ) Dakle, traženi je limes 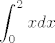 , a to je negdje , a to je negdje  . . 
Što se tiče 2.41. a), razuman hint mi se čini da izlučiš  iz donjeg korijena, a nakon toga izvedeš supstituciju iz donjeg korijena, a nakon toga izvedeš supstituciju 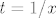 , u kojem trenutku dobivaš da želiš integrirati , u kojem trenutku dobivaš da želiš integrirati 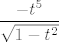 . Sad trigonometrija ima smisla, ne? . Sad trigonometrija ima smisla, ne? 
Što se tiče 2.89., malo je teško objasniti bez crteža, ali ja bih išao ovako. Pretpostavljam da radimo samo s "desnom kružnicom" (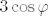 napravi dvije kružnice za napravi dvije kružnice za 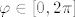 ). Ako ne, slična, tj. potpuno ista, stvar se može napraviti za lijevu kružnicu. ). Ako ne, slična, tj. potpuno ista, stvar se može napraviti za lijevu kružnicu.
Okej, zanima nas samo površina iznad  -osi. (Površina s druge strane je ista, pa samo množimo s -osi. (Površina s druge strane je ista, pa samo množimo s  .) .)
E, sad, odredimo gdje se sijeku kružnica i kardioida. (Samo treba riješiti 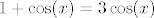 ). Ispada da to rade u ). Ispada da to rade u 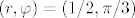 . .
Sad, izračunaj površinu kardioide za 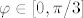 . Za to imaš formulu. Preostaje još dodati onaj mali dio kružnice "lijevo" od kardioide. No, to nam nije teško. Znamo da je to zapravo šestina površine kružnice umanjena za površinu trokuta kojeg omeđuju ishodište, središte kružnice (što je . Za to imaš formulu. Preostaje još dodati onaj mali dio kružnice "lijevo" od kardioide. No, to nam nije teško. Znamo da je to zapravo šestina površine kružnice umanjena za površinu trokuta kojeg omeđuju ishodište, središte kružnice (što je 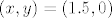 ) i točka ) i točka 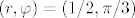 . Radi se o jednakostraničnom trokutu, pa je njegovu površinu još posebno lako izračunati. . Radi se o jednakostraničnom trokutu, pa je njegovu površinu još posebno lako izračunati.
E, tako, sad sve to oduzmeš, zbrojiš i sl. i gotovi smo.  Nisam tu baš puno objašnjavao, možda sam negdje i pogriješio, možda treba malo razmisliti (zašto je to jednakostranični trokut, zašto je ono šestina površine kružnice itd.), ali nadam se da je ovo korektan, dapače, solidan hint. Nisam tu baš puno objašnjavao, možda sam negdje i pogriješio, možda treba malo razmisliti (zašto je to jednakostranični trokut, zašto je ono šestina površine kružnice itd.), ali nadam se da je ovo korektan, dapače, solidan hint. 
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
Dofalol
Forumaš(ica)

Pridružen/a: 24. 10. 2010. (21:25:31)
Postovi: (15)16
Spol: 
|
 Postano: 12:42 sri, 18. 5. 2011 Naslov: Postano: 12:42 sri, 18. 5. 2011 Naslov: |
    |
|
|
[quote="mornik"]Što se tiče 2.8. a), radi se o običnoj integralnoj sumi funkcije [latex]f(x)=x[/latex] na segmentu [latex][0,2][/latex], do na jednu začkoljicu: dodaj na početku u sumu [latex]\displaystyle\frac{2n}{n^2}[/latex] (treba nam za vrijednost koja pripada zadnjem intervalu u subdiviziji). To ide u [latex]0[/latex], pa nikako ne mijenja postojanje niti sumu limesa.[/quote]
Meni se čini da bi bilo korektnije dodati [latex]\displaystyle\frac{0}{n^2}[/latex] na početak sume.
Mislim, tako sam ja. Integralna suma tako ostaje ista, kao i subdivizija, a stvarno nismo mijenjali početnu sumu .
P.S. Rješenje je [latex]\displaystyle\int_{0}^{2}xdx \ = \ 2[/latex]. :D
| mornik (napisa): | Što se tiče 2.8. a), radi se o običnoj integralnoj sumi funkcije 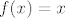 na segmentu na segmentu 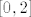 , do na jednu začkoljicu: dodaj na početku u sumu , do na jednu začkoljicu: dodaj na početku u sumu 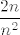 (treba nam za vrijednost koja pripada zadnjem intervalu u subdiviziji). To ide u (treba nam za vrijednost koja pripada zadnjem intervalu u subdiviziji). To ide u  , pa nikako ne mijenja postojanje niti sumu limesa. , pa nikako ne mijenja postojanje niti sumu limesa. |
Meni se čini da bi bilo korektnije dodati 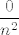 na početak sume. na početak sume.
Mislim, tako sam ja. Integralna suma tako ostaje ista, kao i subdivizija, a stvarno nismo mijenjali početnu sumu .
P.S. Rješenje je 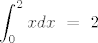 . . 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 18:53 sri, 18. 5. 2011 Naslov: Postano: 18:53 sri, 18. 5. 2011 Naslov: |
    |
|
|
Bah... napisao sam "negdje [latex]1[/latex]". [latex]2[/latex] je negdje [latex]1[/latex]. :) ([latex]2[/latex] je ponegdje i [latex]2[/latex], ali to me se ne tiče. :D) Što se tiče toga što dodajemo, obje su opcije jednako korektne, budući da se lako vidi da dodavanjem [latex]\displaystyle\frac{2n}{n^2}[/latex] ne mijenjamo limes. Sad, što je intuitivnije, to je već druga stvar. :P
Bah... napisao sam "negdje  ". ".  je negdje je negdje  . .  ( ( je ponegdje i je ponegdje i  , ali to me se ne tiče. , ali to me se ne tiče.  ) Što se tiče toga što dodajemo, obje su opcije jednako korektne, budući da se lako vidi da dodavanjem ) Što se tiče toga što dodajemo, obje su opcije jednako korektne, budući da se lako vidi da dodavanjem 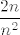 ne mijenjamo limes. Sad, što je intuitivnije, to je već druga stvar. ne mijenjamo limes. Sad, što je intuitivnije, to je već druga stvar. 
|
|
| [Vrh] |
|
rain
Forumaš(ica)

Pridružen/a: 02. 04. 2011. (13:58:42)
Postovi: (13)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 6:56 ned, 22. 5. 2011 Naslov: Postano: 6:56 ned, 22. 5. 2011 Naslov: |
    |
|
|
Čuj, što se WolframAlphe tiče, ne mogu pomoći - površina trokuta čak i [url=http://www.wolframalpha.com/input/?i=area+of+polygon+%280%2C-3%29%2C+%283%2C0%29%2C+%283%2F2%2C3%29]može[/url], za dalje ne znam, možda i svi poligoni idu na taj način...
A što se zadatka tiče, ponovno ne mogu puno pomoći: išao sam rješavati i rješenje je točno. Specifično, ja sam riješio tako da sam izračunao površinu trokuta kojeg rade dvije točke spomenute u zadatku i sjecište tangenti (to je na linku gore), a onda od toga oduzeo površinu "u presjeku" parabole i tog trokuta (to je zapravo integral od [latex](-x^2+4x-3)-(x-3)[/latex] od [latex]0[/latex] do [latex]3[/latex]. Dobije se, kao što rekoh, korektan rezultat. :)
Ne mogu komentirati tvoje rješenje jer ne mogu reći da ga baš shvaćam. :P Možda da probaš ponovno objasniti, ako te veseli. :) Naime, ne vidim nikako zašto računaš površinu koju zatvara parabola s osima (osi u množini, dakle, pretpostavljam, objema osima) kad [latex]y[/latex]-os nema veze sa zadatkom (nema ni [latex]x[/latex]-os, doduše :D). Dapače, ne vidim baš ni kako to činiš jer ne vidim koju površinu zatvara s osima (vidim samo površinu koju zatvara s [latex]x[/latex]-osi). Također, spominješ samo jednu tangentu, a njih su dvije, tako da me i to malo zbunjuje... :)
Čuj, što se WolframAlphe tiče, ne mogu pomoći - površina trokuta čak i može, za dalje ne znam, možda i svi poligoni idu na taj način...
A što se zadatka tiče, ponovno ne mogu puno pomoći: išao sam rješavati i rješenje je točno. Specifično, ja sam riješio tako da sam izračunao površinu trokuta kojeg rade dvije točke spomenute u zadatku i sjecište tangenti (to je na linku gore), a onda od toga oduzeo površinu "u presjeku" parabole i tog trokuta (to je zapravo integral od 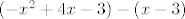 od od  do do 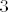 . Dobije se, kao što rekoh, korektan rezultat. . Dobije se, kao što rekoh, korektan rezultat. 
Ne mogu komentirati tvoje rješenje jer ne mogu reći da ga baš shvaćam.  Možda da probaš ponovno objasniti, ako te veseli. Možda da probaš ponovno objasniti, ako te veseli.  Naime, ne vidim nikako zašto računaš površinu koju zatvara parabola s osima (osi u množini, dakle, pretpostavljam, objema osima) kad Naime, ne vidim nikako zašto računaš površinu koju zatvara parabola s osima (osi u množini, dakle, pretpostavljam, objema osima) kad  -os nema veze sa zadatkom (nema ni -os nema veze sa zadatkom (nema ni  -os, doduše -os, doduše  ). Dapače, ne vidim baš ni kako to činiš jer ne vidim koju površinu zatvara s osima (vidim samo površinu koju zatvara s ). Dapače, ne vidim baš ni kako to činiš jer ne vidim koju površinu zatvara s osima (vidim samo površinu koju zatvara s  -osi). Također, spominješ samo jednu tangentu, a njih su dvije, tako da me i to malo zbunjuje... -osi). Također, spominješ samo jednu tangentu, a njih su dvije, tako da me i to malo zbunjuje... 
|
|
| [Vrh] |
|
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
|
| [Vrh] |
|
Tomy007
Forumaš(ica)

Pridružen/a: 08. 11. 2009. (19:45:28)
Postovi: (94)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
A-tom
Forumaš(ica)

Pridružen/a: 18. 05. 2010. (22:18:01)
Postovi: (AB)16
Spol: 
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
|
| [Vrh] |
|
Boris B.
Forumaš(ica)

Pridružen/a: 19. 01. 2010. (18:01:54)
Postovi: (32)16
Spol: 
|
 Postano: 21:01 čet, 26. 5. 2011 Naslov: Postano: 21:01 čet, 26. 5. 2011 Naslov: |
    |
|
|
[quote="Phoenix"]Izraz unutar integrala je zapravo jednak [latex]\frac{\sqrt{ctg(x)}}{\sqrt{2}}[/latex][/quote]
Na polovici svoje prirodne domene je :) Inače nije.
Problem je što je kada su i sinus i kosinus negativni donji korijen definiran, a cijeli izraz očito negativan. No za negativne brojeve ne vrijedi sqrt(ab) = sqrt(a)sqrt(b) (npr. 1 = sqrt(-1 * -1) =/= i^2 = -1), pa zbog toga dobivamo izraz iste apsolutne vrijednosti, ali krivog predznaka (sqrt(ctg x / 2), što je uvijek pozitivno)
Prva funkcija: [url]http://www.wolframalpha.com/input/?i=cos+x+%2F+sqrt%28sin+2x%29[/url]
Druga funkcija: [url]http://www.wolframalpha.com/input/?i=sqrt%28cot+x+%2F+2%29[/url]
Dakle, ovdje bi zapravo trebalo integral rastaviti na dva slučaja, ili se ograničiti samo na jednu komponentu domene, npr. prvi kvadrant (x iz <0, pi/2>)
| Phoenix (napisa): | Izraz unutar integrala je zapravo jednak 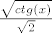 |
Na polovici svoje prirodne domene je  Inače nije. Inače nije.
Problem je što je kada su i sinus i kosinus negativni donji korijen definiran, a cijeli izraz očito negativan. No za negativne brojeve ne vrijedi sqrt(ab) = sqrt(a)sqrt(b) (npr. 1 = sqrt(-1 * -1) =/= i^2 = -1), pa zbog toga dobivamo izraz iste apsolutne vrijednosti, ali krivog predznaka (sqrt(ctg x / 2), što je uvijek pozitivno)
Prva funkcija: http://www.wolframalpha.com/input/?i=cos+x+%2F+sqrt%28sin+2x%29
Druga funkcija: http://www.wolframalpha.com/input/?i=sqrt%28cot+x+%2F+2%29
Dakle, ovdje bi zapravo trebalo integral rastaviti na dva slučaja, ili se ograničiti samo na jednu komponentu domene, npr. prvi kvadrant (x iz <0, pi/2>)
_________________
The lyf so short, the craft so long to lerne
|
|
| [Vrh] |
|
meda
Forumaš(ica)

Pridružen/a: 09. 01. 2010. (09:29:23)
Postovi: (A0)16
|
|
| [Vrh] |
|
|













