| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
sparkle_
Forumaš(ica)
Pridružen/a: 13. 02. 2011. (11:08:40)
Postovi: (E)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
goranm
Forumaš(ica)
Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 6:03 čet, 26. 5. 2011 Naslov: |
    |
|
|
Pa i ne postoji neko detaljnije objašnjenje. Kod x^3+6x^2 + 27x + 42, prosti djelitelji od 42 su 2, 3 i 7. Za p=3 vrijedi da p dijeli a0, a1 i a2, ne dijeli a3 i p^2=9 ne dijeli 42. Iz Eisensteinovog kriterija slijedi da je taj polinom ireducibilan u Q[x].
Kod polinoma 3x^3 + 7x^2 + 3x + 2 Eisensteinov kriterij ne prolazi jer jedini prosti broj koji dijeli slobodni koeficijent je 2, ali 2 ne dijeli a1. Ostaje vidjeti da li ima racionalne nultočke, a kandidati za te nultočke su cjelobrojni djelitelji slobodnog koeficijenta i svi racionalni brojevi oblika p/q gdje p dijeli slobodan, a q vodeći koeficijent. Moguće nultočke su tada [latex]\left\{\pm 1,\pm 2, \pm 1/3, \pm 2/3 \right\}[/latex]. S obzirom da niti jedan od tih brojeva ne poništava polinom, tada se on u Q[x] ne može rastaviti na polinome manjeg stupnja, tj. ireducibilan je u Q[x].
Pa i ne postoji neko detaljnije objašnjenje. Kod x^3+6x^2 + 27x + 42, prosti djelitelji od 42 su 2, 3 i 7. Za p=3 vrijedi da p dijeli a0, a1 i a2, ne dijeli a3 i p^2=9 ne dijeli 42. Iz Eisensteinovog kriterija slijedi da je taj polinom ireducibilan u Q[x].
Kod polinoma 3x^3 + 7x^2 + 3x + 2 Eisensteinov kriterij ne prolazi jer jedini prosti broj koji dijeli slobodni koeficijent je 2, ali 2 ne dijeli a1. Ostaje vidjeti da li ima racionalne nultočke, a kandidati za te nultočke su cjelobrojni djelitelji slobodnog koeficijenta i svi racionalni brojevi oblika p/q gdje p dijeli slobodan, a q vodeći koeficijent. Moguće nultočke su tada 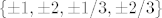 . S obzirom da niti jedan od tih brojeva ne poništava polinom, tada se on u Q[x] ne može rastaviti na polinome manjeg stupnja, tj. ireducibilan je u Q[x].
_________________
The Dude Abides
|
|
| [Vrh] |
|
sunce
Forumaš(ica)
Pridružen/a: 20. 03. 2010. (18:49:03)
Postovi: (3F)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
ankovacic
Forumaš(ica)
Pridružen/a: 27. 10. 2009. (19:28:17)
Postovi: (5C)16
Spol: 
|
| Postano: 8:12 ned, 29. 5. 2011 Naslov: |
|
|
|
Imam neke nejasnoce oko jednog zadatka sa vježbi:
Dakle promatramo Z[i], i rekli smo da je M(3, i)=1, ali:
3/i=3/i * i/i=-3i € Z[i] => i|3 u Z[i] => M(3, i)=i;
Jedino što smo vezno rekli u Z[i] da su invertibilni elementi u Z[i]={+i, -i, 1, -1}; istina je da je (1)=(i)=Z[i], ali definitivno ne vrijedi i=1;
Pa ako bi mi neko mogao objasnit kako M(3, i)=1
Imam neke nejasnoce oko jednog zadatka sa vježbi:
Dakle promatramo Z[i], i rekli smo da je M(3, i)=1, ali:
3/i=3/i * i/i=-3i € Z[i] ⇒ i|3 u Z[i] ⇒ M(3, i)=i;
Jedino što smo vezno rekli u Z[i] da su invertibilni elementi u Z[i]={+i, -i, 1, -1}; istina je da je (1)=(i)=Z[i], ali definitivno ne vrijedi i=1;
Pa ako bi mi neko mogao objasnit kako M(3, i)=1
|
|
| [Vrh] |
|
maty321
Forumaš(ica)
Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
|
| [Vrh] |
|
some_dude
Forumaš(ica)
Pridružen/a: 08. 11. 2009. (16:23:13)
Postovi: (59)16
Spol:
Lokacija: Zd-Zg
|
| Postano: 12:52 ned, 29. 5. 2011 Naslov: |
|
|
[quote="ankovacic"]Imam neke nejasnoce oko jednog zadatka sa vježbi:
Dakle promatramo Z[i], i rekli smo da je M(3, i)=1, ali:
3/i=3/i * i/i=-3i € Z[i] => i|3 u Z[i] => M(3, i)=i;
Jedino što smo vezno rekli u Z[i] da su invertibilni elementi u Z[i]={+i, -i, 1, -1}; istina je da je (1)=(i)=Z[i], ali definitivno ne vrijedi i=1;
Pa ako bi mi neko mogao objasnit kako M(3, i)=1[/quote]
Za DGI A vrijedi da za svaki a,b iz A postoji NZM(a,b) t.d. <a,b> = <NZM(a,b)>. Nema jedinstvenosti. Zato vrijedi M(3,i) = i i M(3,i) = 1. | ankovacic (napisa): | Imam neke nejasnoce oko jednog zadatka sa vježbi:
Dakle promatramo Z[i], i rekli smo da je M(3, i)=1, ali:
3/i=3/i * i/i=-3i € Z[i] ⇒ i|3 u Z[i] ⇒ M(3, i)=i;
Jedino što smo vezno rekli u Z[i] da su invertibilni elementi u Z[i]={+i, -i, 1, -1}; istina je da je (1)=(i)=Z[i], ali definitivno ne vrijedi i=1;
Pa ako bi mi neko mogao objasnit kako M(3, i)=1 |
Za DGI A vrijedi da za svaki a,b iz A postoji NZM(a,b) t.d. <a,b> = <NZM(a,b)>. Nema jedinstvenosti. Zato vrijedi M(3,i) = i i M(3,i) = 1.
|
|
| [Vrh] |
|
goranm
Forumaš(ica)
Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol:
|
| Postano: 17:18 ned, 29. 5. 2011 Naslov: |
|
|
|
[quote="ankovacic"]Imam neke nejasnoce oko jednog zadatka sa vježbi:
Dakle promatramo Z[i], i rekli smo da je M(3, i)=1, ali:
3/i=3/i * i/i=-3i € Z[i] => i|3 u Z[i] => M(3, i)=i;
Jedino što smo vezno rekli u Z[i] da su invertibilni elementi u Z[i]={+i, -i, 1, -1}; istina je da je (1)=(i)=Z[i], ali definitivno ne vrijedi i=1;
Pa ako bi mi neko mogao objasnit kako M(3, i)=1[/quote]
To vrijedi jer svaki asociran element od NZD(a,b) je opet NZD(a,b) (to slijedi iz definicije NZD u komutativnom prstenu).
U komutativnom prstenu s jedinicom vrijedi ako je a=br, pri čemu je r invertibilan, onda su a i b asocirani. Dakle, ako je NZD(3,1)=1, onda će vrijediti i NZD(3,1)=-1, NZD(3,1)=i, NZD(3,1)=-i jer je 1=-1*(-1)=i*(-i)=-i*i.
| ankovacic (napisa): | Imam neke nejasnoce oko jednog zadatka sa vježbi:
Dakle promatramo Z[i], i rekli smo da je M(3, i)=1, ali:
3/i=3/i * i/i=-3i € Z[i] ⇒ i|3 u Z[i] ⇒ M(3, i)=i;
Jedino što smo vezno rekli u Z[i] da su invertibilni elementi u Z[i]={+i, -i, 1, -1}; istina je da je (1)=(i)=Z[i], ali definitivno ne vrijedi i=1;
Pa ako bi mi neko mogao objasnit kako M(3, i)=1 |
To vrijedi jer svaki asociran element od NZD(a,b) je opet NZD(a,b) (to slijedi iz definicije NZD u komutativnom prstenu).
U komutativnom prstenu s jedinicom vrijedi ako je a=br, pri čemu je r invertibilan, onda su a i b asocirani. Dakle, ako je NZD(3,1)=1, onda će vrijediti i NZD(3,1)=-1, NZD(3,1)=i, NZD(3,1)=-i jer je 1=-1*(-1)=i*(-i)=-i*i.
_________________
The Dude Abides
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)
Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
weeh
Forumaš(ica)
Pridružen/a: 29. 10. 2008. (00:00:53)
Postovi: (32)16
Spol:
Lokacija: Zagreb
|
|
| [Vrh] |
|
homesweethome
Forumaš(ica)
Pridružen/a: 21. 10. 2009. (16:25:25)
Postovi: (1C)16
|
| Postano: 17:25 pon, 30. 5. 2011 Naslov: |
|
|
|
[quote="goranm"]Pa i ne postoji neko detaljnije objašnjenje. Kod x^3+6x^2 + 27x + 42, prosti djelitelji od 42 su 2, 3 i 7. Za p=3 vrijedi da p dijeli a0, a1 i a2, ne dijeli a3 i p^2=9 ne dijeli 42. Iz Eisensteinovog kriterija slijedi da je taj polinom ireducibilan u Q[x].
Kod polinoma 3x^3 + 7x^2 + 3x + 2 Eisensteinov kriterij ne prolazi jer jedini prosti broj koji dijeli slobodni koeficijent je 2, ali 2 ne dijeli a1. Ostaje vidjeti da li ima racionalne nultočke, a kandidati za te nultočke su cjelobrojni djelitelji slobodnog koeficijenta i svi racionalni brojevi oblika p/q gdje p dijeli slobodan, a q vodeći koeficijent. Moguće nultočke su tada [latex]\left\{\pm 1,\pm 2, \pm 1/3, \pm 2/3 \right\}[/latex]. S obzirom da niti jedan od tih brojeva ne poništava polinom, tada se on u Q[x] ne može rastaviti na polinome manjeg stupnja, tj. ireducibilan je u Q[x].[/quote]
da ali zar u kriteriju ne pise da ti elementi moraju biti ireducibilni u Q, a po definiciji npr. 3 nije ireducibilan( invertibilan je u Q) ? ili?
| goranm (napisa): | Pa i ne postoji neko detaljnije objašnjenje. Kod x^3+6x^2 + 27x + 42, prosti djelitelji od 42 su 2, 3 i 7. Za p=3 vrijedi da p dijeli a0, a1 i a2, ne dijeli a3 i p^2=9 ne dijeli 42. Iz Eisensteinovog kriterija slijedi da je taj polinom ireducibilan u Q[x].
Kod polinoma 3x^3 + 7x^2 + 3x + 2 Eisensteinov kriterij ne prolazi jer jedini prosti broj koji dijeli slobodni koeficijent je 2, ali 2 ne dijeli a1. Ostaje vidjeti da li ima racionalne nultočke, a kandidati za te nultočke su cjelobrojni djelitelji slobodnog koeficijenta i svi racionalni brojevi oblika p/q gdje p dijeli slobodan, a q vodeći koeficijent. Moguće nultočke su tada 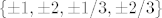. S obzirom da niti jedan od tih brojeva ne poništava polinom, tada se on u Q[x] ne može rastaviti na polinome manjeg stupnja, tj. ireducibilan je u Q[x]. |
da ali zar u kriteriju ne pise da ti elementi moraju biti ireducibilni u Q, a po definiciji npr. 3 nije ireducibilan( invertibilan je u Q) ? ili?
|
|
| [Vrh] |
|
goranm
Forumaš(ica)
Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol:
|
| Postano: 18:37 pon, 30. 5. 2011 Naslov: |
|
|
|
[quote="homesweethome"]da ali zar u kriteriju ne pise da ti elementi moraju biti ireducibilni u Q, a po definiciji npr. 3 nije ireducibilan( invertibilan je u Q) ? ili?[/quote]
Ne, ne piše. Kriterij glasi: neka je D domena jedinstvene faktorizacije i F kvocijentno polje od D. Ako je f polinom u [b]D[x][/b] i p je [b]ireducibilan element od D[/b] td. p ne dijeli a_n, p^2 ne dijeli a_0 i p dijeli a_i za i=0,...,n-1, onda je f ireducibilan u [b]F[x][/b] (uz dodatak: ako je f primitivan, onda je ireducibilan i u D[x]).
U ovom slučaju kriterij se primijenjuje za D=Z, F=Q i p iz D=Z ireducibilan(=prost) i tako se pokaže da je f ireducibilan u F[x]=Q[x].
| homesweethome (napisa): | | da ali zar u kriteriju ne pise da ti elementi moraju biti ireducibilni u Q, a po definiciji npr. 3 nije ireducibilan( invertibilan je u Q) ? ili? |
Ne, ne piše. Kriterij glasi: neka je D domena jedinstvene faktorizacije i F kvocijentno polje od D. Ako je f polinom u D[x] i p je ireducibilan element od D td. p ne dijeli a_n, p^2 ne dijeli a_0 i p dijeli a_i za i=0,...,n-1, onda je f ireducibilan u F[x] (uz dodatak: ako je f primitivan, onda je ireducibilan i u D[x]).
U ovom slučaju kriterij se primijenjuje za D=Z, F=Q i p iz D=Z ireducibilan(=prost) i tako se pokaže da je f ireducibilan u F[x]=Q[x].
_________________
The Dude Abides
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)
Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
patlidzan
Forumaš(ica)
Pridružen/a: 05. 11. 2009. (19:17:28)
Postovi: (76)16
Spol:
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)
Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol:
Lokacija: Over the roof
|
|
| [Vrh] |
|
homesweethome
Forumaš(ica)
Pridružen/a: 21. 10. 2009. (16:25:25)
Postovi: (1C)16
|
| Postano: 19:40 pon, 30. 5. 2011 Naslov: |
|
|
|
[quote="goranm"][quote="homesweethome"]da ali zar u kriteriju ne pise da ti elementi moraju biti ireducibilni u Q, a po definiciji npr. 3 nije ireducibilan( invertibilan je u Q) ? ili?[/quote]
Ne, ne piše. Kriterij glasi: neka je D domena jedinstvene faktorizacije i F kvocijentno polje od D. Ako je f polinom u [b]D[x][/b] i p je [b]ireducibilan element od D[/b] td. p ne dijeli a_n, p^2 ne dijeli a_0 i p dijeli a_i za i=0,...,n-1, onda je f ireducibilan u [b]F[x][/b] (uz dodatak: ako je f primitivan, onda je ireducibilan i u D[x]).
U ovom slučaju kriterij se primijenjuje za D=Z, F=Q i p iz D=Z ireducibilan(=prost) i tako se pokaže da je f ireducibilan u F[x]=Q[x].[/quote]
:D hvala
| goranm (napisa): | | homesweethome (napisa): | | da ali zar u kriteriju ne pise da ti elementi moraju biti ireducibilni u Q, a po definiciji npr. 3 nije ireducibilan( invertibilan je u Q) ? ili? |
Ne, ne piše. Kriterij glasi: neka je D domena jedinstvene faktorizacije i F kvocijentno polje od D. Ako je f polinom u D[x] i p je ireducibilan element od D td. p ne dijeli a_n, p^2 ne dijeli a_0 i p dijeli a_i za i=0,...,n-1, onda je f ireducibilan u F[x] (uz dodatak: ako je f primitivan, onda je ireducibilan i u D[x]).
U ovom slučaju kriterij se primijenjuje za D=Z, F=Q i p iz D=Z ireducibilan(=prost) i tako se pokaže da je f ireducibilan u F[x]=Q[x]. |
 hvala
|
|
| [Vrh] |
|
kaj
Forumaš(ica)
Pridružen/a: 15. 11. 2009. (21:02:20)
Postovi: (B8)16
|
|
| [Vrh] |
|
|
