| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
Boris B.
Forumaš(ica)

Pridružen/a: 19. 01. 2010. (18:01:54)
Postovi: (32)16
Spol: 
|
 Postano: 14:34 sub, 4. 6. 2011 Naslov: Postano: 14:34 sub, 4. 6. 2011 Naslov: |
    |
|
|
[quote="Tomislav"]Slight offtopic: Bas gledam zadatke iz redova s prijasnjih kolokvija, i svaki 2-3 mi se cini uzasno tezak, npr 3.a) proslogodisnji...za njega imam rješenje, ali je za doci do njega trebalo puuuno vremena, koje nemam na kolokviju, tako da kao da ga nisam ni rijesio. Ima li netko neko "jednostavno" rjesenje za taj zadatak? Takodjer ja i kolega nismo uspjeli pokazati da je niz [latex]a_n=\frac{arctg(n!)}{n}[/latex] strogo padajuc, pa ako netko to zna, neka napise.[/quote]
Meni padaju na pamet dva načina za riješiti... sad, pošto se oba kind of baziraju na integralnim sumama, ne znam koliko su tipična i koliko koje od njih dugo traje... prvi je rutinski i recimo intuitivno jasan ako znaš ideju (a korisna je).
[latex]\sum_{k = 1}^n \sqrt n[/latex] shvati kao površinu n pravokutnika širine 1, a visine korijen k, za k od 1 do n. Kad to nacrtaš, recimo počevši s 1x1 pravokutnikom u ishodištu, odmah vidiš da možeš povući dvije krivulje, jednu kroz gornje lijeve, a drugu kroz gornje desne vrhove, između kojih je ova površina smještena. Ovako nekako: [odi na alfu i ubaci Plot[{Sqrt[Ceiling[n]], Sqrt[n], Sqrt[n + 1]}, {n, 0, 9}], što iz nepoznatoga razloga ne mogu linkati ovdje]
Jednadžbe krivulja su naravno [latex]\sqrt x[/latex] i [latex]\sqrt {x+1}[/latex], a kako je "površina" sume manja od površine ispod druge, a veća od površine ispod prve, onda se nalazi između njihovih integrala, koji su nešto reda veličine n^3/2, što rješava zadatak usporednim kriterijem.
Naravno, ovo je sada na razini "očito je sa slike", što vjerojatno nije dovoljan argument :D ali formalizirati stvar je jednostavno koristeći nejednakost [latex]n \leq \lceil x\rceil \leq n+1[/latex], iz koje po monotonosti integrala, i integrabilnosti funkcije "strop" (konačan broj prekida) slijedi da je njen integral između integrala onih dviju korijena. A kao što i očekujemo imamo [latex]\int_0^n \sqrt{\lceil x \rceil} dx = \sum_{k=1}^n \int_{k-1}^k \sqrt{\lceil x \rceil} dx = \sum_{k=1}^n \int_{k-1}^k \sqrt k dx = \sum_{k=1}^n \sqrt k[/latex].
Alternativno i možda jednostavnije je zbog monotonosti korijena, suma korijena donja integralna suma korijena x+1, a gornja korijena x, pa nejednakost int1 <= suma <= int2 slijedi iz toga.
E sad, za napisat ovo ne treba više od 10 min, al koliko treba za sjetiti se ne znam :) no ovakvo ocjenjivanje sume sa dva integrala je korisno općenito i može se jednostavno napraviti za bilo koju monotonu funkciju, analogno ovome.
Drugi način je manje motiviran i više mehanički, ali možda brži, ne znam.
Sastoji se od toga da odlučiš od [latex]\sum_{k=1}^n \sqrt k[/latex] napraviti integralnu sumu i onda radiš sve što trebaš da je stvarno i dobiješ. Što se svede na: [latex]\sum_{k=1}^n \sqrt k = \sqrt n \sum_{k=1}^n \sqrt {k/n} = n \sqrt n (\frac 1 n \sum_{k=1}^n \sqrt {k/n})[/latex], gdje je ovo u zagradi u limesu = [latex]\int_0^1 \sqrt x dx[/latex]. Sad, koja je poanta toga? Poanta je da je da smo dobili n korijen n * (izraz koji u limesu ide u 2/3), dakle da je član našega početnoga reda reda veličine 1/(n korijen n), što po onom kvocijentnom kriteriju (ako se tako zove?) implicira da red konvergira (pošto 1/(n korijen n) = 1 / n^(3/2) konvergira, jer je 3/2 > 1).
Izostavljeni su rutinskiji detalji, ali pitaj ako koji treba napisati.
Za ovo s arctg-om, jel trebalo baš pokazati da je niz padajuć, ili je zadatak nešto drugo, u rješavanju čega bi ovo bio jedan korak?
| Tomislav (napisa): | Slight offtopic: Bas gledam zadatke iz redova s prijasnjih kolokvija, i svaki 2-3 mi se cini uzasno tezak, npr 3.a) proslogodisnji...za njega imam rješenje, ali je za doci do njega trebalo puuuno vremena, koje nemam na kolokviju, tako da kao da ga nisam ni rijesio. Ima li netko neko "jednostavno" rjesenje za taj zadatak? Takodjer ja i kolega nismo uspjeli pokazati da je niz 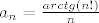 strogo padajuc, pa ako netko to zna, neka napise. strogo padajuc, pa ako netko to zna, neka napise. |
Meni padaju na pamet dva načina za riješiti... sad, pošto se oba kind of baziraju na integralnim sumama, ne znam koliko su tipična i koliko koje od njih dugo traje... prvi je rutinski i recimo intuitivno jasan ako znaš ideju (a korisna je).
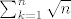 shvati kao površinu n pravokutnika širine 1, a visine korijen k, za k od 1 do n. Kad to nacrtaš, recimo počevši s 1x1 pravokutnikom u ishodištu, odmah vidiš da možeš povući dvije krivulje, jednu kroz gornje lijeve, a drugu kroz gornje desne vrhove, između kojih je ova površina smještena. Ovako nekako: [odi na alfu i ubaci Plot[{Sqrt[Ceiling[n]], Sqrt[n], Sqrt[n + 1]}, {n, 0, 9}], što iz nepoznatoga razloga ne mogu linkati ovdje] shvati kao površinu n pravokutnika širine 1, a visine korijen k, za k od 1 do n. Kad to nacrtaš, recimo počevši s 1x1 pravokutnikom u ishodištu, odmah vidiš da možeš povući dvije krivulje, jednu kroz gornje lijeve, a drugu kroz gornje desne vrhove, između kojih je ova površina smještena. Ovako nekako: [odi na alfu i ubaci Plot[{Sqrt[Ceiling[n]], Sqrt[n], Sqrt[n + 1]}, {n, 0, 9}], što iz nepoznatoga razloga ne mogu linkati ovdje]
Jednadžbe krivulja su naravno 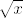 i i 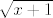 , a kako je "površina" sume manja od površine ispod druge, a veća od površine ispod prve, onda se nalazi između njihovih integrala, koji su nešto reda veličine n^3/2, što rješava zadatak usporednim kriterijem. , a kako je "površina" sume manja od površine ispod druge, a veća od površine ispod prve, onda se nalazi između njihovih integrala, koji su nešto reda veličine n^3/2, što rješava zadatak usporednim kriterijem.
Naravno, ovo je sada na razini "očito je sa slike", što vjerojatno nije dovoljan argument  ali formalizirati stvar je jednostavno koristeći nejednakost ali formalizirati stvar je jednostavno koristeći nejednakost 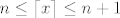 , iz koje po monotonosti integrala, i integrabilnosti funkcije "strop" (konačan broj prekida) slijedi da je njen integral između integrala onih dviju korijena. A kao što i očekujemo imamo , iz koje po monotonosti integrala, i integrabilnosti funkcije "strop" (konačan broj prekida) slijedi da je njen integral između integrala onih dviju korijena. A kao što i očekujemo imamo 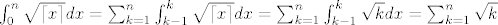 . .
Alternativno i možda jednostavnije je zbog monotonosti korijena, suma korijena donja integralna suma korijena x+1, a gornja korijena x, pa nejednakost int1 ⇐ suma ⇐ int2 slijedi iz toga.
E sad, za napisat ovo ne treba više od 10 min, al koliko treba za sjetiti se ne znam  no ovakvo ocjenjivanje sume sa dva integrala je korisno općenito i može se jednostavno napraviti za bilo koju monotonu funkciju, analogno ovome. no ovakvo ocjenjivanje sume sa dva integrala je korisno općenito i može se jednostavno napraviti za bilo koju monotonu funkciju, analogno ovome.
Drugi način je manje motiviran i više mehanički, ali možda brži, ne znam.
Sastoji se od toga da odlučiš od 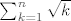 napraviti integralnu sumu i onda radiš sve što trebaš da je stvarno i dobiješ. Što se svede na: napraviti integralnu sumu i onda radiš sve što trebaš da je stvarno i dobiješ. Što se svede na: 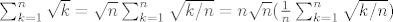 , gdje je ovo u zagradi u limesu = , gdje je ovo u zagradi u limesu = 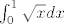 . Sad, koja je poanta toga? Poanta je da je da smo dobili n korijen n * (izraz koji u limesu ide u 2/3), dakle da je član našega početnoga reda reda veličine 1/(n korijen n), što po onom kvocijentnom kriteriju (ako se tako zove?) implicira da red konvergira (pošto 1/(n korijen n) = 1 / n^(3/2) konvergira, jer je 3/2 > 1). . Sad, koja je poanta toga? Poanta je da je da smo dobili n korijen n * (izraz koji u limesu ide u 2/3), dakle da je član našega početnoga reda reda veličine 1/(n korijen n), što po onom kvocijentnom kriteriju (ako se tako zove?) implicira da red konvergira (pošto 1/(n korijen n) = 1 / n^(3/2) konvergira, jer je 3/2 > 1).
Izostavljeni su rutinskiji detalji, ali pitaj ako koji treba napisati.
Za ovo s arctg-om, jel trebalo baš pokazati da je niz padajuć, ili je zadatak nešto drugo, u rješavanju čega bi ovo bio jedan korak?
_________________
The lyf so short, the craft so long to lerne
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
maaajčiii
Forumaš(ica)

Pridružen/a: 05. 01. 2011. (12:11:11)
Postovi: (2D)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 18:49 sub, 4. 6. 2011 Naslov: Postano: 18:49 sub, 4. 6. 2011 Naslov: |
    |
|
|
Rekao bih da su stvari razumno standardne, pa će možda samo hint biti dovoljan - u a) i b) dijelu, rastavi stvar po parcijalnim razlomcima, a nakon toga koristi razvoj od [latex]\ln(1+x)[/latex] i [latex]\arctg(x)[/latex], uz [latex]x=1[/latex] i/ili [latex]x=-1[/latex]. To bi moglo biti korisno. :) (Then again, možda i nije, ništa ne jamčim. :D)
U e) dijelu, ideja je isto dosta jasna - nekako prijeći iz [latex]n[/latex] u nazivniku u [latex]n^2[/latex]. U tu svrhu, integriraj [latex]\ln(1+x)/x[/latex]. Nakon toga, uzmi [latex]x=1/3[/latex]. Aha, da. Moje isprike. Tu imamo sitan problem i iskreno ne znam kako ga riješiti: naime, pronaći formulu u elementarnim funkcijama od [latex]\ln(1+x)/x[/latex], čini se, ne ide. :( Također, [url=http://www.wolframalpha.com/input/?i=-Li_2%28-1%2F3%29]rješenje[/url] je u decimalnom zapisu (a zbilja se radi o tom broju - pogledaj pri dnu stranice "series representation") iznimno ružno. Esencijalno, radi se o [url=http://en.wikipedia.org/wiki/Polylogarithm]polilogaritmu[/url]. Stoga, ne znam baš može li se dobiti zatvorena formula za ovaj zadatak - možda i može. Hm. :?
Rekao bih da su stvari razumno standardne, pa će možda samo hint biti dovoljan - u a) i b) dijelu, rastavi stvar po parcijalnim razlomcima, a nakon toga koristi razvoj od 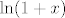 i i 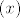 , uz , uz  i/ili i/ili  . To bi moglo biti korisno. . To bi moglo biti korisno.  (Then again, možda i nije, ništa ne jamčim. (Then again, možda i nije, ništa ne jamčim.  ) )
U e) dijelu, ideja je isto dosta jasna - nekako prijeći iz  u nazivniku u u nazivniku u 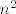 . U tu svrhu, integriraj . U tu svrhu, integriraj 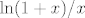 . Nakon toga, uzmi . Nakon toga, uzmi 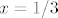 . Aha, da. Moje isprike. Tu imamo sitan problem i iskreno ne znam kako ga riješiti: naime, pronaći formulu u elementarnim funkcijama od . Aha, da. Moje isprike. Tu imamo sitan problem i iskreno ne znam kako ga riješiti: naime, pronaći formulu u elementarnim funkcijama od 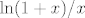 , čini se, ne ide. , čini se, ne ide.  Također, rješenje je u decimalnom zapisu (a zbilja se radi o tom broju - pogledaj pri dnu stranice "series representation") iznimno ružno. Esencijalno, radi se o polilogaritmu. Stoga, ne znam baš može li se dobiti zatvorena formula za ovaj zadatak - možda i može. Hm. Također, rješenje je u decimalnom zapisu (a zbilja se radi o tom broju - pogledaj pri dnu stranice "series representation") iznimno ružno. Esencijalno, radi se o polilogaritmu. Stoga, ne znam baš može li se dobiti zatvorena formula za ovaj zadatak - možda i može. Hm. 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 10:12 ned, 5. 6. 2011 Naslov: Postano: 10:12 ned, 5. 6. 2011 Naslov: |
    |
|
|
[quote="Tomislav"][quote="frutabella"]
E, jel moze taj pod a) ici ovako, ja ne vidim zasto ne bi mogao:
neka je an= cijeli onaj izraz sume, a bn=1/korjen(n)
Buduci su an i bn redovi s pozitivnim clanovima i vrijedi:
L=lim (n--->besk) an/bn = 1,
a bn je divergentan -----> an divergentan :D :D :D[/quote]
Stvar je u tome da limes [latex]\frac{1+\sqrt{2}+...+\sqrt{n}}{\sqrt{n}}[/latex] nikako nije [latex]1[/latex] :wink:[/quote]
an= 1/[ korjen(1)+korjen(2)+korjen(3)...+korjen(n)]
bn= 1/ korjen(n)
an/bn= korjen(n) / [ korjen(1)+korjen(2)+korjen(3)+...+korjen(n) ]
sve kad podijelis sa korjen(n) dobijes
1/ [ korjen(1)/kor(n) + kor(2)/kor(n) ... + 1 = pustis limes, sve ide u 0 (zasto ne ide??? ), ostaje samo 1. :D
| Tomislav (napisa): | | frutabella (napisa): |
E, jel moze taj pod a) ici ovako, ja ne vidim zasto ne bi mogao:
neka je an= cijeli onaj izraz sume, a bn=1/korjen(n)
Buduci su an i bn redovi s pozitivnim clanovima i vrijedi:
L=lim (n→besk) an/bn = 1,
a bn je divergentan -----> an divergentan    |
Stvar je u tome da limes 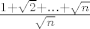 nikako nije nikako nije   |
an= 1/[ korjen(1)+korjen(2)+korjen(3)...+korjen(n)]
bn= 1/ korjen(n)
an/bn= korjen(n) / [ korjen(1)+korjen(2)+korjen(3)+...+korjen(n) ]
sve kad podijelis sa korjen(n) dobijes
1/ [ korjen(1)/kor(n) + kor(2)/kor(n) ... + 1 = pustis limes, sve ide u 0 (zasto ne ide??? ), ostaje samo 1. 
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
 Postano: 10:28 ned, 5. 6. 2011 Naslov: Postano: 10:28 ned, 5. 6. 2011 Naslov: |
    |
|
|
To je jako krivo i nematematicko razmisljanje. Nemozes tako olako shvacati beskonacnost.
Iako nevolim ovakve kontraprimjere pisat, napravit cu iznimku.
[latex]1=\frac{n}{n}=\frac{1+1+...+1+1}{n}[/latex] gdje u brojniku ima [latex]n[/latex] jedinica. Sad dijeli sa [latex]n[/latex] pa dobijes:
[latex]\frac{\frac{1}{n}+...+\frac{1}{n}}{1}[/latex]. Brojnik ocito ide u [latex]0[/latex] pa je limes [latex]0[/latex]. Upravo smo pokazali da je [latex]1=0[/latex] i srusili cijelu matematiku, fiziku, kemiju, biologiju, brojanje ovaca na poljani, broj zrtava u ratu, itd itd.
P.S. Zasto ne koristiti wolframalpha i vidjeti da limes nikako nije [latex]1[/latex]? :x
To je jako krivo i nematematicko razmisljanje. Nemozes tako olako shvacati beskonacnost.
Iako nevolim ovakve kontraprimjere pisat, napravit cu iznimku.
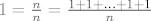 gdje u brojniku ima gdje u brojniku ima  jedinica. Sad dijeli sa jedinica. Sad dijeli sa  pa dobijes: pa dobijes:
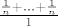 . Brojnik ocito ide u . Brojnik ocito ide u  pa je limes pa je limes  . Upravo smo pokazali da je . Upravo smo pokazali da je  i srusili cijelu matematiku, fiziku, kemiju, biologiju, brojanje ovaca na poljani, broj zrtava u ratu, itd itd. i srusili cijelu matematiku, fiziku, kemiju, biologiju, brojanje ovaca na poljani, broj zrtava u ratu, itd itd.
P.S. Zasto ne koristiti wolframalpha i vidjeti da limes nikako nije  ? ? 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
888
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (18:26:14)
Postovi: (29)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
Boris B.
Forumaš(ica)

Pridružen/a: 19. 01. 2010. (18:01:54)
Postovi: (32)16
Spol: 
|
|
| [Vrh] |
|
maaajčiii
Forumaš(ica)

Pridružen/a: 05. 01. 2011. (12:11:11)
Postovi: (2D)16
|
 Postano: 17:15 ned, 5. 6. 2011 Naslov: Postano: 17:15 ned, 5. 6. 2011 Naslov: |
    |
|
|
[quote="mornik"]Rekao bih da su stvari razumno standardne, pa će možda samo hint biti dovoljan - u a) i b) dijelu, rastavi stvar po parcijalnim razlomcima, a nakon toga koristi razvoj od [latex]\ln(1+x)[/latex] i [latex]\arctg(x)[/latex], uz [latex]x=1[/latex] i/ili [latex]x=-1[/latex]. To bi moglo biti korisno. :) (Then again, možda i nije, ništa ne jamčim. :D)
U e) dijelu, ideja je isto dosta jasna - nekako prijeći iz [latex]n[/latex] u nazivniku u [latex]n^2[/latex]. U tu svrhu, integriraj [latex]\ln(1+x)/x[/latex]. Nakon toga, uzmi [latex]x=1/3[/latex]. Aha, da. Moje isprike. Tu imamo sitan problem i iskreno ne znam kako ga riješiti: naime, pronaći formulu u elementarnim funkcijama od [latex]\ln(1+x)/x[/latex], čini se, ne ide. :( Također, [url=http://www.wolframalpha.com/input/?i=-Li_2%28-1%2F3%29]rješenje[/url] je u decimalnom zapisu (a zbilja se radi o tom broju - pogledaj pri dnu stranice "series representation") iznimno ružno. Esencijalno, radi se o [url=http://en.wikipedia.org/wiki/Polylogarithm]polilogaritmu[/url]. Stoga, ne znam baš može li se dobiti zatvorena formula za ovaj zadatak - možda i može. Hm. :?[/quote]
hvala ti!
| mornik (napisa): | Rekao bih da su stvari razumno standardne, pa će možda samo hint biti dovoljan - u a) i b) dijelu, rastavi stvar po parcijalnim razlomcima, a nakon toga koristi razvoj od 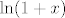 i i 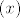 , uz , uz  i/ili i/ili  . To bi moglo biti korisno. . To bi moglo biti korisno.  (Then again, možda i nije, ništa ne jamčim. (Then again, možda i nije, ništa ne jamčim.  ) )
U e) dijelu, ideja je isto dosta jasna - nekako prijeći iz  u nazivniku u u nazivniku u 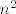 . U tu svrhu, integriraj . U tu svrhu, integriraj 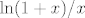 . Nakon toga, uzmi . Nakon toga, uzmi 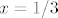 . Aha, da. Moje isprike. Tu imamo sitan problem i iskreno ne znam kako ga riješiti: naime, pronaći formulu u elementarnim funkcijama od . Aha, da. Moje isprike. Tu imamo sitan problem i iskreno ne znam kako ga riješiti: naime, pronaći formulu u elementarnim funkcijama od 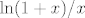 , čini se, ne ide. , čini se, ne ide.  Također, rješenje je u decimalnom zapisu (a zbilja se radi o tom broju - pogledaj pri dnu stranice "series representation") iznimno ružno. Esencijalno, radi se o polilogaritmu. Stoga, ne znam baš može li se dobiti zatvorena formula za ovaj zadatak - možda i može. Hm. Također, rješenje je u decimalnom zapisu (a zbilja se radi o tom broju - pogledaj pri dnu stranice "series representation") iznimno ružno. Esencijalno, radi se o polilogaritmu. Stoga, ne znam baš može li se dobiti zatvorena formula za ovaj zadatak - možda i može. Hm.  |
hvala ti!
|
|
| [Vrh] |
|
piccola
Forumaš(ica)

Pridružen/a: 30. 11. 2009. (15:39:50)
Postovi: (D7)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
piccola
Forumaš(ica)

Pridružen/a: 30. 11. 2009. (15:39:50)
Postovi: (D7)16
|
|
| [Vrh] |
|
meda
Forumaš(ica)

Pridružen/a: 09. 01. 2010. (09:29:23)
Postovi: (A0)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
Joker
Forumaš(ica)

Pridružen/a: 19. 09. 2010. (10:19:16)
Postovi: (8C)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
|












