| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
tomitza
Forumaš(ica)


Pridružen/a: 28. 11. 2008. (19:50:48)
Postovi: (58)16
|
 Postano: 23:03 ned, 12. 6. 2011 Naslov: Postano: 23:03 ned, 12. 6. 2011 Naslov: |
    |
|
|
[quote="Anonymous"]a u prvoj grupi imamo: 1/(z-1)^2.. Da li sada radimo ovako: znamo da je to derivacija od -1/z-1 --> to razvijemo, pa onda deriviramo clan po clan, ili isto samo na kraju pomnozimo s 1/(z-1)^2?[/quote]
ne, ne radis tako :)
dakle, imas:
[latex]f(z)=\frac{1}{(z-1)^2(z-4)(z-2)}[/latex]
rastaviš [latex]\frac{1}{(z-4)(z-2)}[/latex] na parcijalne razlomke
dobiješ [latex]\frac{1}{2(z-4)}-\frac{1}{2(z-2)}[/latex]
onda svaki od njih razviješ u Laurentov red oko 1
[latex]\frac{1}{(z-4)}=-\frac{1}{3}\frac{1}{1-\frac{z-1}{3}}=-\sum_{n=0}^{\infty}\frac{(z-1)^n}{3^{n+1}}[/latex] to možeš jer je kružnom vijencu [latex]\left |{\frac{z-1}{3}}\right | <1[/latex]
[latex]\frac{1}{(z-2)}=\frac{1}{z-1}\frac{1}{1-\frac{1}{z-1}}=\sum_{n=0}^{\infty}\frac{1}{(z-1)^{n+1}}}[/latex] to možeš jer je kružnom vijencu [latex]\left |{\frac{1}{z-1}}\right | <1[/latex]
i sad te sume pomnožiš sa [latex]\frac{1}{(z-1)^2}[/latex], središ ih i to je to :)
| Anonymous (napisa): | | a u prvoj grupi imamo: 1/(z-1)^2.. Da li sada radimo ovako: znamo da je to derivacija od -1/z-1 → to razvijemo, pa onda deriviramo clan po clan, ili isto samo na kraju pomnozimo s 1/(z-1)^2? |
ne, ne radis tako 
dakle, imas:
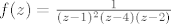
rastaviš 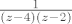 na parcijalne razlomke na parcijalne razlomke
dobiješ 
onda svaki od njih razviješ u Laurentov red oko 1
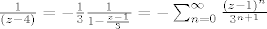 to možeš jer je kružnom vijencu to možeš jer je kružnom vijencu 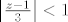
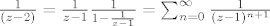 to možeš jer je kružnom vijencu to možeš jer je kružnom vijencu 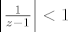
i sad te sume pomnožiš sa  , središ ih i to je to , središ ih i to je to 
|
|
| [Vrh] |
|
Gost
|
 Postano: 23:20 ned, 12. 6. 2011 Naslov: Postano: 23:20 ned, 12. 6. 2011 Naslov: |
    |
|
|
[quote="tomitza"][quote="Anonymous"]a u prvoj grupi imamo: 1/(z-1)^2.. Da li sada radimo ovako: znamo da je to derivacija od -1/z-1 --> to razvijemo, pa onda deriviramo clan po clan, ili isto samo na kraju pomnozimo s 1/(z-1)^2?[/quote]
ne, ne radis tako :)
dakle, imas:
[latex]f(z)=\frac{1}{(z-1)^2(z-4)(z-2)}[/latex]
rastaviš [latex]\frac{1}{(z-4)(z-2)}[/latex] na parcijalne razlomke
dobiješ [latex]\frac{1}{2(z-4)}-\frac{1}{2(z-2)}[/latex]
onda svaki od njih razviješ u Laurentov red oko 1
[latex]\frac{1}{(z-4)}=-\frac{1}{3}\frac{1}{1-\frac{z-1}{3}}=-\sum_{n=0}^{\infty}\frac{(z-1)^n}{3^{n+1}}[/latex] to možeš jer je kružnom vijencu [latex]\left |{\frac{z-1}{3}}\right | <1[/latex]
[latex]\frac{1}{(z-2)}=\frac{1}{z-1}\frac{1}{1-\frac{1}{z-1}}=\sum_{n=0}^{\infty}\frac{1}{(z-1)^{n+1}}}[/latex] to možeš jer je kružnom vijencu [latex]\left |{\frac{1}{z-1}}\right | <1[/latex]
i sad te sume pomnožiš sa [latex]\frac{1}{(z-1)^2}[/latex], središ ih i to je to :)[/quote]
Hvala puno!!
L.red oko točke i na podrucju koje sadrzi tocku 2i od fje f(z)=1/((z-i)^15(z^2-1))
Bi li mogao raspisati..
| tomitza (napisa): | | Anonymous (napisa): | | a u prvoj grupi imamo: 1/(z-1)^2.. Da li sada radimo ovako: znamo da je to derivacija od -1/z-1 → to razvijemo, pa onda deriviramo clan po clan, ili isto samo na kraju pomnozimo s 1/(z-1)^2? |
ne, ne radis tako 
dakle, imas:
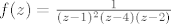
rastaviš 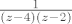 na parcijalne razlomke na parcijalne razlomke
dobiješ 
onda svaki od njih razviješ u Laurentov red oko 1
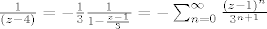 to možeš jer je kružnom vijencu to možeš jer je kružnom vijencu 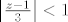
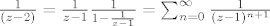 to možeš jer je kružnom vijencu to možeš jer je kružnom vijencu 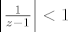
i sad te sume pomnožiš sa  , središ ih i to je to , središ ih i to je to  |
Hvala puno!!
L.red oko točke i na podrucju koje sadrzi tocku 2i od fje f(z)=1/((z-i)^15(z^2-1))
Bi li mogao raspisati..
|
|
| [Vrh] |
|
tomitza
Forumaš(ica)


Pridružen/a: 28. 11. 2008. (19:50:48)
Postovi: (58)16
|
 Postano: 23:47 ned, 12. 6. 2011 Naslov: Postano: 23:47 ned, 12. 6. 2011 Naslov: |
    |
|
|
[latex]f(z)=\frac{1}{(z-1)^15(z^2-1)}[/latex]
razvijaš u Laurentov red na probušenom krugu oko [latex]i[/latex] radijusa [latex]\sqrt{2}[/latex], dakle [latex]V=\left \{ 0<\left | z-1 \right | \right \} < 1[/latex]. Dakle, to područje sadrži točku [latex]2i[/latex], a ne sadrži singularitete, koji su u točkama [latex]-1,1[/latex].
I sad radiš analogno ovome gore, rastaviš [latex]\frac{1}{z^2-1}[/latex] na parcijalne razlomke [latex]\frac{1}{(z-1)}-\frac{1}{(z+1)}[/latex], razviješ to u red oko [latex]i[/latex], i pomnožiš na kraju sa [latex]\frac{1}{(z-i)^{15}}[/latex]...
recimo
[latex]\frac{1}{(z+1)}=\frac{1}{(z-i)+1+i}=\frac{1}{1+i}\frac{1}{\frac{z-i}{1+i}+1}=\sum_{n=0}^{\infty}\frac{(z-i)^n}{(1+i)^{n+1}}}[/latex] to možeš jer je na probušenom krugu [latex]\left |{\frac{z-i}{1+i}}\right | <1[/latex] jer je [latex]\left | z-i \right | <\left | 1+i \right |=\sqrt{2}[/latex]. Primijeti da je sve vrlo lijepo naštimano. :)
za [latex]\frac{1}{(z-1)} [/latex] radiš potpuno analogno...

razvijaš u Laurentov red na probušenom krugu oko  radijusa radijusa 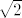 , dakle , dakle 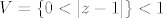 . Dakle, to područje sadrži točku . Dakle, to područje sadrži točku 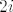 , a ne sadrži singularitete, koji su u točkama , a ne sadrži singularitete, koji su u točkama 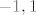 . .
I sad radiš analogno ovome gore, rastaviš 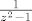 na parcijalne razlomke na parcijalne razlomke  , razviješ to u red oko , razviješ to u red oko  , i pomnožiš na kraju sa , i pomnožiš na kraju sa 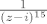 ... ...
recimo
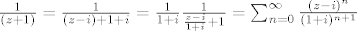 to možeš jer je na probušenom krugu to možeš jer je na probušenom krugu 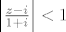 jer je jer je 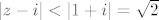 . Primijeti da je sve vrlo lijepo naštimano. . Primijeti da je sve vrlo lijepo naštimano. 
za 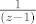 radiš potpuno analogno... radiš potpuno analogno...
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Alisa
Forumaš(ica)
Pridružen/a: 16. 02. 2008. (15:34:59)
Postovi: (4E)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
ivy=)
Forumaš(ica)
Pridružen/a: 03. 11. 2007. (14:00:45)
Postovi: (34)16
|
|
| [Vrh] |
|
pmfovka
Forumaš(ica)
Pridružen/a: 08. 11. 2009. (21:58:15)
Postovi: (60)16
|
|
| [Vrh] |
|
mililimi
Forumaš(ica)
Pridružen/a: 18. 06. 2005. (13:33:48)
Postovi: (6D)16
|
|
| [Vrh] |
|
slash
Forumaš(ica)
Pridružen/a: 20. 02. 2008. (18:17:24)
Postovi: (39)16
|
|
| [Vrh] |
|
mery
Forumaš(ica)

Pridružen/a: 01. 12. 2008. (21:57:21)
Postovi: (43)16
|
|
| [Vrh] |
|
|





