|
Pa i nije da baš odmah ispadnu iz definicije. :D Evo par uputa.
1° Tu je bitno iskoristiti da, ako parametriziraš [latex]\partial I^2[/latex] pozitivno s [latex]\gamma_1[/latex], [latex]\gamma_2[/latex], [latex]\gamma_3[/latex] i [latex]\gamma_4[/latex], slijedi da [latex]F \circ \gamma_1[/latex], [latex]F \circ \gamma_2[/latex], [latex]F \circ \gamma_3[/latex] i [latex]F \circ \gamma_4[/latex] pozitivno parametriziraju [latex]\partial D[/latex]. Raspišeš obje strane, i na kraju dobiš istu stvar (da, ima se za pisati).
2° Ovaj dio čak direktno slijedi iz teorema o zamjeni varijabli.
3° Ovog sam počeo raspisivati, ali sam odustao i zaključio da je lakši općenitiji dokaz (za k-forme). :)
Pa i nije da baš odmah ispadnu iz definicije.  Evo par uputa. Evo par uputa.
1° Tu je bitno iskoristiti da, ako parametriziraš 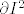 pozitivno s pozitivno s 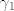 , , 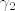 , , 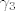 i i 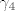 , slijedi da , slijedi da 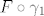 , , 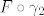 , , 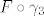 i i 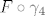 pozitivno parametriziraju pozitivno parametriziraju 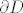 . Raspišeš obje strane, i na kraju dobiš istu stvar (da, ima se za pisati). . Raspišeš obje strane, i na kraju dobiš istu stvar (da, ima se za pisati).
2° Ovaj dio čak direktno slijedi iz teorema o zamjeni varijabli.
3° Ovog sam počeo raspisivati, ali sam odustao i zaključio da je lakši općenitiji dokaz (za k-forme). 
|





