| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
princeza_fiona
Forumaš(ica)

Pridružen/a: 26. 01. 2011. (13:22:44)
Postovi: (B)16
Spol: 
|
|
| [Vrh] |
|
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 15:14 sri, 26. 1. 2011 Naslov: Postano: 15:14 sri, 26. 1. 2011 Naslov: |
    |
|
|
Na predavanju smo pokazali neprekidnost funkcije [latex]\sqrt[n]{x}[/latex]. Dokaz za [latex]\sqrt{x}[/latex] je samo poseban slučaj kada uvrštavaš [latex]n=2[/latex], pa je priča sasvim ista.
Računam da imaš bilješke s predavanja (lakše je pratiti gradivo i kontinuitet s njima), pa ću o neprekidnosti ukratko u crticama.
Dakle, promatramo funkciju [latex]x^{2}[/latex]. Pokazali smo da je na intervalu [latex]\left\langle 0, +\infty \right\rangle[/latex] strogo rastuća, a kako je neprekidna na cijeloj svojoj domeni, posebno je neprekidna i na ovom intervalu. Budući da je to otvoreni interval u širem smislu, slika funkcije restringirane na taj interval je također otvoreni interval u širem smislu (to je poznati teorem), a s obzirom da je funkcija [latex]x^{2}[/latex] strogo rastuća, rubne vrijednosti njene slike saznat ćemo promatrajući u što teži funkcijska vrijednost kada [latex]x[/latex] teži u [latex]0[/latex], odnosno u [latex]+\infty[/latex]. Time se pokaže da je slika također [latex]\left\langle 0, +\infty \right\rangle[/latex]. Dakle, funkcija [latex]f(x)=x^2[/latex] definirana kao [latex]f|_{\left\langle 0, +\infty \right\rangle}:\left\langle 0, +\infty \right\rangle \rightarrow \left\langle 0, +\infty \right\rangle[/latex] je strogo rastuća bijekcija. Sada je inverz (definiran kao korijen - što mu je zapravo dosad bilo "samo ime") također definiran na otvorenom intervalu, slika mu je otvoreni interval te je istog tipa monotonosti kao i početna funkcija (propozicija s početka semestra). Po drugom poznatom teoremu znamo da je ova funkcija neprekidna.
Funkcija se još može proširiti u točki [latex](0,0)[/latex] tako da dokažemo: ako [latex]\sqrt{x}[/latex] teži u [latex]0[/latex], onda [latex]x[/latex] teži u [latex]0[/latex]. To je napisano na predavanju: pretpostavi se suprotno i lako se pokaže kontradikcija preko epsilona. :)
Eto, ovo je otprilike "neformalan" "dokaz" općenito za bilo koji [latex]\sqrt[n]{x}[/latex] (a u ovom primjeru posebno za [latex]\sqrt{x}[/latex]). Za neparne [latex]n[/latex] se na sličan način proširi funkcija s [latex]\mathbb{R}[/latex] na [latex]\mathbb{R}[/latex].
Znam da je preopširno i dosta zbunjujuće jer sam se potrudio napisati samo bitne misli, kao i njihov tok. Dobro pročitaj riječ po riječ jer je argumentacija jako bitna i još malo usporedi s bilježnicom. Pitaj ako nešto nije jasno. :)
Na predavanju smo pokazali neprekidnost funkcije 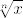 . Dokaz za . Dokaz za 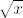 je samo poseban slučaj kada uvrštavaš je samo poseban slučaj kada uvrštavaš  , pa je priča sasvim ista. , pa je priča sasvim ista.
Računam da imaš bilješke s predavanja (lakše je pratiti gradivo i kontinuitet s njima), pa ću o neprekidnosti ukratko u crticama.
Dakle, promatramo funkciju 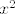 . Pokazali smo da je na intervalu . Pokazali smo da je na intervalu 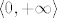 strogo rastuća, a kako je neprekidna na cijeloj svojoj domeni, posebno je neprekidna i na ovom intervalu. Budući da je to otvoreni interval u širem smislu, slika funkcije restringirane na taj interval je također otvoreni interval u širem smislu (to je poznati teorem), a s obzirom da je funkcija strogo rastuća, a kako je neprekidna na cijeloj svojoj domeni, posebno je neprekidna i na ovom intervalu. Budući da je to otvoreni interval u širem smislu, slika funkcije restringirane na taj interval je također otvoreni interval u širem smislu (to je poznati teorem), a s obzirom da je funkcija 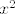 strogo rastuća, rubne vrijednosti njene slike saznat ćemo promatrajući u što teži funkcijska vrijednost kada strogo rastuća, rubne vrijednosti njene slike saznat ćemo promatrajući u što teži funkcijska vrijednost kada  teži u teži u  , odnosno u , odnosno u  . Time se pokaže da je slika također . Time se pokaže da je slika također 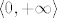 . Dakle, funkcija . Dakle, funkcija 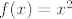 definirana kao definirana kao 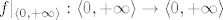 je strogo rastuća bijekcija. Sada je inverz (definiran kao korijen - što mu je zapravo dosad bilo "samo ime") također definiran na otvorenom intervalu, slika mu je otvoreni interval te je istog tipa monotonosti kao i početna funkcija (propozicija s početka semestra). Po drugom poznatom teoremu znamo da je ova funkcija neprekidna. je strogo rastuća bijekcija. Sada je inverz (definiran kao korijen - što mu je zapravo dosad bilo "samo ime") također definiran na otvorenom intervalu, slika mu je otvoreni interval te je istog tipa monotonosti kao i početna funkcija (propozicija s početka semestra). Po drugom poznatom teoremu znamo da je ova funkcija neprekidna.
Funkcija se još može proširiti u točki 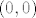 tako da dokažemo: ako tako da dokažemo: ako 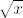 teži u teži u  , onda , onda  teži u teži u  . To je napisano na predavanju: pretpostavi se suprotno i lako se pokaže kontradikcija preko epsilona. . To je napisano na predavanju: pretpostavi se suprotno i lako se pokaže kontradikcija preko epsilona. 
Eto, ovo je otprilike "neformalan" "dokaz" općenito za bilo koji 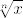 (a u ovom primjeru posebno za (a u ovom primjeru posebno za 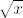 ). Za neparne ). Za neparne  se na sličan način proširi funkcija s se na sličan način proširi funkcija s  na na  . .
Znam da je preopširno i dosta zbunjujuće jer sam se potrudio napisati samo bitne misli, kao i njihov tok. Dobro pročitaj riječ po riječ jer je argumentacija jako bitna i još malo usporedi s bilježnicom. Pitaj ako nešto nije jasno. 
|
|
| [Vrh] |
|
Annemarie
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (19:45:56)
Postovi: (62)16
|
|
| [Vrh] |
|
antemijoc1991
Forumaš(ica)

Pridružen/a: 03. 10. 2010. (14:54:35)
Postovi: (6)16
|
|
| [Vrh] |
|
princeza_fiona
Forumaš(ica)

Pridružen/a: 26. 01. 2011. (13:22:44)
Postovi: (B)16
Spol: 
|
 Postano: 20:01 sri, 26. 1. 2011 Naslov: Postano: 20:01 sri, 26. 1. 2011 Naslov: |
    |
|
|
[quote="Phoenix"]Na predavanju smo pokazali neprekidnost funkcije [latex]\sqrt[n]{x}[/latex]. Dokaz za [latex]\sqrt{x}[/latex] je samo poseban slučaj kada uvrštavaš [latex]n=2[/latex], pa je priča sasvim ista.
Računam da imaš bilješke s predavanja (lakše je pratiti gradivo i kontinuitet s njima), pa ću o neprekidnosti ukratko u crticama.
Dakle, promatramo funkciju [latex]x^{2}[/latex]. Pokazali smo da je na intervalu [latex]\left\langle 0, +\infty \right\rangle[/latex] strogo rastuća, a kako je neprekidna na cijeloj svojoj domeni, posebno je neprekidna i na ovom intervalu. Budući da je to otvoreni interval u širem smislu, slika funkcije restringirane na taj interval je također otvoreni interval u širem smislu (to je poznati teorem), a s obzirom da je funkcija [latex]x^{2}[/latex] strogo rastuća, rubne vrijednosti njene slike saznat ćemo promatrajući u što teži funkcijska vrijednost kada [latex]x[/latex] teži u [latex]0[/latex], odnosno u [latex]+\infty[/latex]. Time se pokaže da je slika također [latex]\left\langle 0, +\infty \right\rangle[/latex]. Dakle, funkcija [latex]f(x)=x^2[/latex] definirana kao [latex]f|_{\left\langle 0, +\infty \right\rangle}:\left\langle 0, +\infty \right\rangle \rightarrow \left\langle 0, +\infty \right\rangle[/latex] je strogo rastuća bijekcija. Sada je inverz (definiran kao korijen - što mu je zapravo dosad bilo "samo ime") također definiran na otvorenom intervalu, slika mu je otvoreni interval te je istog tipa monotonosti kao i početna funkcija (propozicija s početka semestra). Po drugom poznatom teoremu znamo da je ova funkcija neprekidna.
Funkcija se još može proširiti u točki [latex](0,0)[/latex] tako da dokažemo: ako [latex]\sqrt{x}[/latex] teži u [latex]0[/latex], onda [latex]x[/latex] teži u [latex]0[/latex]. To je napisano na predavanju: pretpostavi se suprotno i lako se pokaže kontradikcija preko epsilona. :)
Eto, ovo je otprilike "neformalan" "dokaz" općenito za bilo koji [latex]\sqrt[n]{x}[/latex] (a u ovom primjeru posebno za [latex]\sqrt{x}[/latex]). Za neparne [latex]n[/latex] se na sličan način proširi funkcija s [latex]\mathbb{R}[/latex] na [latex]\mathbb{R}[/latex].
Znam da je preopširno i dosta zbunjujuće jer sam se potrudio napisati samo bitne misli, kao i njihov tok. Dobro pročitaj riječ po riječ jer je argumentacija jako bitna i još malo usporedi s bilježnicom. Pitaj ako nešto nije jasno. :)[/quote]
hvala ti puno :))
imala sam nešto tako u glavi samo nisam znala odakle bi počela,al' sad mi je puno jasnije :lol:
a treba li dokazivat da je x^2 injekcija,surjekcija(dakle bijekcija) pa da onda po tom postoji inverz?
[size=9][color=#999999]Added after 2 minutes:[/color][/size]
[quote="Lepi91"][quote="princeza_fiona"]bi li netko mogao napisati formalni dokaz da je (2.)korijen iz x neprekidna funkcija...barem hintove... :roll:[/quote]
neznam sad kak tocno ide...al uzmes funkciju x^2
i sad ona ti je bijekcija na nula do plus besk. i sad da bi izrazili neprekidnost inverza moramo prosirit funkciju na x^2 za x>=0 x za x<=0
i sad po teoremu o neprekidnosti inverza na 0 do plus beskonacno korijen x je neprekidna...tak nekak bi isla ideja...
imas taj dokaz u guljasevoj skripti,mislim na 80.stranici ak se ne varam...[/quote]
hvala :D
| Phoenix (napisa): | Na predavanju smo pokazali neprekidnost funkcije 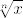 . Dokaz za . Dokaz za 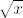 je samo poseban slučaj kada uvrštavaš je samo poseban slučaj kada uvrštavaš  , pa je priča sasvim ista. , pa je priča sasvim ista.
Računam da imaš bilješke s predavanja (lakše je pratiti gradivo i kontinuitet s njima), pa ću o neprekidnosti ukratko u crticama.
Dakle, promatramo funkciju 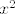 . Pokazali smo da je na intervalu . Pokazali smo da je na intervalu 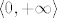 strogo rastuća, a kako je neprekidna na cijeloj svojoj domeni, posebno je neprekidna i na ovom intervalu. Budući da je to otvoreni interval u širem smislu, slika funkcije restringirane na taj interval je također otvoreni interval u širem smislu (to je poznati teorem), a s obzirom da je funkcija strogo rastuća, a kako je neprekidna na cijeloj svojoj domeni, posebno je neprekidna i na ovom intervalu. Budući da je to otvoreni interval u širem smislu, slika funkcije restringirane na taj interval je također otvoreni interval u širem smislu (to je poznati teorem), a s obzirom da je funkcija 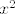 strogo rastuća, rubne vrijednosti njene slike saznat ćemo promatrajući u što teži funkcijska vrijednost kada strogo rastuća, rubne vrijednosti njene slike saznat ćemo promatrajući u što teži funkcijska vrijednost kada  teži u teži u  , odnosno u , odnosno u  . Time se pokaže da je slika također . Time se pokaže da je slika također 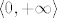 . Dakle, funkcija . Dakle, funkcija 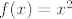 definirana kao definirana kao 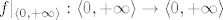 je strogo rastuća bijekcija. Sada je inverz (definiran kao korijen - što mu je zapravo dosad bilo "samo ime") također definiran na otvorenom intervalu, slika mu je otvoreni interval te je istog tipa monotonosti kao i početna funkcija (propozicija s početka semestra). Po drugom poznatom teoremu znamo da je ova funkcija neprekidna. je strogo rastuća bijekcija. Sada je inverz (definiran kao korijen - što mu je zapravo dosad bilo "samo ime") također definiran na otvorenom intervalu, slika mu je otvoreni interval te je istog tipa monotonosti kao i početna funkcija (propozicija s početka semestra). Po drugom poznatom teoremu znamo da je ova funkcija neprekidna.
Funkcija se još može proširiti u točki 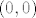 tako da dokažemo: ako tako da dokažemo: ako 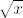 teži u teži u  , onda , onda  teži u teži u  . To je napisano na predavanju: pretpostavi se suprotno i lako se pokaže kontradikcija preko epsilona. . To je napisano na predavanju: pretpostavi se suprotno i lako se pokaže kontradikcija preko epsilona. 
Eto, ovo je otprilike "neformalan" "dokaz" općenito za bilo koji 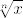 (a u ovom primjeru posebno za (a u ovom primjeru posebno za 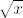 ). Za neparne ). Za neparne  se na sličan način proširi funkcija s se na sličan način proširi funkcija s  na na  . .
Znam da je preopširno i dosta zbunjujuće jer sam se potrudio napisati samo bitne misli, kao i njihov tok. Dobro pročitaj riječ po riječ jer je argumentacija jako bitna i još malo usporedi s bilježnicom. Pitaj ako nešto nije jasno.  |
hvala ti puno  ) )
imala sam nešto tako u glavi samo nisam znala odakle bi počela,al' sad mi je puno jasnije 
a treba li dokazivat da je x^2 injekcija,surjekcija(dakle bijekcija) pa da onda po tom postoji inverz?
Added after 2 minutes:
| Lepi91 (napisa): | | princeza_fiona (napisa): | bi li netko mogao napisati formalni dokaz da je (2.)korijen iz x neprekidna funkcija...barem hintove...  |
neznam sad kak tocno ide...al uzmes funkciju x^2
i sad ona ti je bijekcija na nula do plus besk. i sad da bi izrazili neprekidnost inverza moramo prosirit funkciju na x^2 za x>=0 x za x⇐0
i sad po teoremu o neprekidnosti inverza na 0 do plus beskonacno korijen x je neprekidna...tak nekak bi isla ideja...
imas taj dokaz u guljasevoj skripti,mislim na 80.stranici ak se ne varam... |
hvala 
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 20:16 sri, 26. 1. 2011 Naslov: Postano: 20:16 sri, 26. 1. 2011 Naslov: |
    |
|
|
Naravno, da bi pokazali bijektivnost funkcije, treba pokazati njenu injektivnost i surjektivnost. Ali ako bolje promotriš, i to smo "vješto" pokazali:
1) Funkcija (odnosno restrikcija na intervalu kojeg promatramo) je strogo rastuća (raspis razlike kvadrata i argumentacija za nenegativne vrijednosti), a dokazali smo kratku propoziciju na početku semestra koja kaže: ako je funkcija strogo monotona, onda je injektivna. Iz toga slijedi [b]injektivnost[/b].
2) Pri početku dokaza smo znali da je [latex]R_f \subseteq \mathbb{R}[/latex]. Međutim, poslije smo pokazali da je [latex]f(\left\langle 0, +\infty \right\rangle)=\left\langle 0, +\infty \right\rangle[/latex]. Stoga, ako promatramo funkciju definiranu ovako: [latex]f|_{\left\langle 0, +\infty \right\rangle}:\left\langle 0, +\infty \right\rangle \rightarrow \left\langle 0, +\infty \right\rangle[/latex], tada smo sigurni i u njenu [b]surjektivnost[/b].
Konačno, pokazali smo da je [latex]f|_{\left\langle 0, +\infty \right\rangle}:\left\langle 0, +\infty \right\rangle \rightarrow \left\langle 0, +\infty \right\rangle[/latex] injekcija i surjekcija, stoga je i bijekcija. :)
(Ako je dio za surjektivnost nejasan, evo još detalja: znamo da je slika otvoreni interval zbog teorema kojeg sam naveo. To znači da za svaku vrijednost unutar tog intervala postoji njena vrijednost iz domene, odnosno: [latex](\forall y \in \left\langle 0, +\infty \right\rangle)(\exists x \in \left\langle 0, +\infty \right\rangle) f(x)=y[/latex]. To je zapravo i smisao teorema - da nema broja unutar tih granica za koji ne bi postojao njen [latex]x[/latex] iz domene. :)
Slična stvar je i s primjenom Bolzano-Weierstrassovog teorema za funkcije.)
Naravno, da bi pokazali bijektivnost funkcije, treba pokazati njenu injektivnost i surjektivnost. Ali ako bolje promotriš, i to smo "vješto" pokazali:
1) Funkcija (odnosno restrikcija na intervalu kojeg promatramo) je strogo rastuća (raspis razlike kvadrata i argumentacija za nenegativne vrijednosti), a dokazali smo kratku propoziciju na početku semestra koja kaže: ako je funkcija strogo monotona, onda je injektivna. Iz toga slijedi injektivnost.
2) Pri početku dokaza smo znali da je 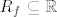 . Međutim, poslije smo pokazali da je . Međutim, poslije smo pokazali da je 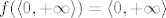 . Stoga, ako promatramo funkciju definiranu ovako: . Stoga, ako promatramo funkciju definiranu ovako: 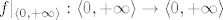 , tada smo sigurni i u njenu surjektivnost. , tada smo sigurni i u njenu surjektivnost.
Konačno, pokazali smo da je 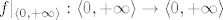 injekcija i surjekcija, stoga je i bijekcija. injekcija i surjekcija, stoga je i bijekcija. 
(Ako je dio za surjektivnost nejasan, evo još detalja: znamo da je slika otvoreni interval zbog teorema kojeg sam naveo. To znači da za svaku vrijednost unutar tog intervala postoji njena vrijednost iz domene, odnosno: 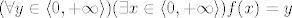 . To je zapravo i smisao teorema - da nema broja unutar tih granica za koji ne bi postojao njen . To je zapravo i smisao teorema - da nema broja unutar tih granica za koji ne bi postojao njen  iz domene. iz domene. 
Slična stvar je i s primjenom Bolzano-Weierstrassovog teorema za funkcije.)
|
|
| [Vrh] |
|
princeza_fiona
Forumaš(ica)

Pridružen/a: 26. 01. 2011. (13:22:44)
Postovi: (B)16
Spol: 
|
|
| [Vrh] |
|
princeza_fiona
Forumaš(ica)

Pridružen/a: 26. 01. 2011. (13:22:44)
Postovi: (B)16
Spol: 
|
 Postano: 22:13 sri, 26. 1. 2011 Naslov: Postano: 22:13 sri, 26. 1. 2011 Naslov: |
    |
|
|
[quote="Phoenix"]Naravno, da bi pokazali bijektivnost funkcije, treba pokazati njenu injektivnost i surjektivnost. Ali ako bolje promotriš, i to smo "vješto" pokazali:
1) Funkcija (odnosno restrikcija na intervalu kojeg promatramo) je strogo rastuća (raspis razlike kvadrata i argumentacija za nenegativne vrijednosti), a dokazali smo kratku propoziciju na početku semestra koja kaže: ako je funkcija strogo monotona, onda je injektivna. Iz toga slijedi [b]injektivnost[/b].
2) Pri početku dokaza smo znali da je [latex]R_f \subseteq \mathbb{R}[/latex]. Međutim, poslije smo pokazali da je [latex]f(\left\langle 0, +\infty \right\rangle)=\left\langle 0, +\infty \right\rangle[/latex]. Stoga, ako promatramo funkciju definiranu ovako: [latex]f|_{\left\langle 0, +\infty \right\rangle}:\left\langle 0, +\infty \right\rangle \rightarrow \left\langle 0, +\infty \right\rangle[/latex], tada smo sigurni i u njenu [b]surjektivnost[/b].
Konačno, pokazali smo da je [latex]f|_{\left\langle 0, +\infty \right\rangle}:\left\langle 0, +\infty \right\rangle \rightarrow \left\langle 0, +\infty \right\rangle[/latex] injekcija i surjekcija, stoga je i bijekcija. :)
(Ako je dio za surjektivnost nejasan, evo još detalja: znamo da je slika otvoreni interval zbog teorema kojeg sam naveo. To znači da za svaku vrijednost unutar tog intervala postoji njena vrijednost iz domene, odnosno: [latex](\forall y \in \left\langle 0, +\infty \right\rangle)(\exists x \in \left\langle 0, +\infty \right\rangle) f(x)=y[/latex]. To je zapravo i smisao teorema - da nema broja unutar tih granica za koji ne bi postojao njen [latex]x[/latex] iz domene. :)
Slična stvar je i s primjenom Bolzano-Weierstrassovog teorema za funkcije.)[/quote]
da,stvarno...pametno :lol:
jasno mi je za surjekciju: kodomena restringirane funkcije je u biti slika te funkcije pa se nema što dokazivat...
puno manje posla nego sam mislila :D
ee i hvala ti još jednom :)
| Phoenix (napisa): | Naravno, da bi pokazali bijektivnost funkcije, treba pokazati njenu injektivnost i surjektivnost. Ali ako bolje promotriš, i to smo "vješto" pokazali:
1) Funkcija (odnosno restrikcija na intervalu kojeg promatramo) je strogo rastuća (raspis razlike kvadrata i argumentacija za nenegativne vrijednosti), a dokazali smo kratku propoziciju na početku semestra koja kaže: ako je funkcija strogo monotona, onda je injektivna. Iz toga slijedi injektivnost.
2) Pri početku dokaza smo znali da je 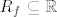 . Međutim, poslije smo pokazali da je . Međutim, poslije smo pokazali da je 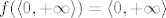 . Stoga, ako promatramo funkciju definiranu ovako: . Stoga, ako promatramo funkciju definiranu ovako: 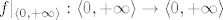 , tada smo sigurni i u njenu surjektivnost. , tada smo sigurni i u njenu surjektivnost.
Konačno, pokazali smo da je 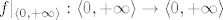 injekcija i surjekcija, stoga je i bijekcija. injekcija i surjekcija, stoga je i bijekcija. 
(Ako je dio za surjektivnost nejasan, evo još detalja: znamo da je slika otvoreni interval zbog teorema kojeg sam naveo. To znači da za svaku vrijednost unutar tog intervala postoji njena vrijednost iz domene, odnosno: 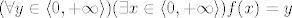 . To je zapravo i smisao teorema - da nema broja unutar tih granica za koji ne bi postojao njen . To je zapravo i smisao teorema - da nema broja unutar tih granica za koji ne bi postojao njen  iz domene. iz domene. 
Slična stvar je i s primjenom Bolzano-Weierstrassovog teorema za funkcije.) |
da,stvarno...pametno 
jasno mi je za surjekciju: kodomena restringirane funkcije je u biti slika te funkcije pa se nema što dokazivat...
puno manje posla nego sam mislila 
ee i hvala ti još jednom 
|
|
| [Vrh] |
|
krasiva
Forumaš(ica)

Pridružen/a: 01. 11. 2010. (23:22:49)
Postovi: (16)16
|
|
| [Vrh] |
|
sparkyca
Forumaš(ica)
Pridružen/a: 10. 06. 2010. (18:54:08)
Postovi: (D)16
|
|
| [Vrh] |
|
stella22
Forumaš(ica)

Pridružen/a: 25. 01. 2011. (11:22:56)
Postovi: (5)16
|
|
| [Vrh] |
|
toy.200
Forumaš(ica)

Pridružen/a: 28. 09. 2010. (14:45:47)
Postovi: (3)16
Spol: 
|
|
| [Vrh] |
|
wannaknow
Forumaš(ica)
Pridružen/a: 07. 09. 2010. (16:38:49)
Postovi: (2C)16
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
sparkyca
Forumaš(ica)
Pridružen/a: 10. 06. 2010. (18:54:08)
Postovi: (D)16
|
|
| [Vrh] |
|
Ilja
Forumaš(ica)

Pridružen/a: 30. 10. 2002. (22:22:31)
Postovi: (1AF)16
|
|
| [Vrh] |
|
Alia3
Forumaš(ica)


Pridružen/a: 14. 01. 2011. (23:07:02)
Postovi: (22)16
Spol: 
|
 Postano: 15:17 sub, 14. 1. 2012 Naslov: Postano: 15:17 sub, 14. 1. 2012 Naslov: |
    |
|
|
Ako bi mogla pomoć oko jednog zadatka,teorijskog,imam ga rješenog ali mi nisu jasne baš sve stvari,ma kako trivijalne bile. Zadatak je dokazati da je [tex] \sqrt[n]{n} [/tex]
[tex] \epsilon>0 [/tex]
[tex](1+\epsilon)^n = 1 + n*\epsilon + \frac{n(n-1)}{2}\epsilon^2 + .... + \epsilon^n \geq \frac{n(n-1)}{2}\epsilon^2 [/tex]
Sad za početak mi nije jasno zašto smo počeli sa [tex](1+\epsilon)^n[/tex],jel samo zato da se poslije naštima na teorem o sendviču tj omeđenost?
Sad provjeravamo dali je [tex]\frac{n-1}{2}\epsilon^2 > 1 [/tex] Zašto baš to??
[tex]\Rightarrow n>1+\frac{2}{\epsilon^2}[/tex]
Po Arhimedovom aksiomu postoji [tex] n_{0}=n_{0}(\epsilon)\in N[/tex] takav da je [tex]n_{0} > 1+\frac{2}{\epsilon^2}[/tex] tj. [tex]\frac{n_{0}-1}{2}\epsilon^2>1[/tex]
[tex]\Rightarrow n\geq n_{0} \Rightarrow (1+\epsilon)^n \geq n(\frac{n-1}{2})\epsilon^2 \geq n(\frac{n_{0}-1}{2})\epsilon^2 > n > 1[/tex]
[tex] (1+\epsilon)^n > n > 1 [/tex] primjenimo n-ti korjen
[tex](1+\epsilon) > \sqrt[n]{n} > 1 [/tex]
[tex]\epsilon > \sqrt[n]{n} > 0 [/tex]
[tex] \mid \sqrt[n]{n} -1 \mid < \epsilon [/tex]
[tex] \Rightarrow \lim \sqrt[n]{n} = 1 [/tex]
Jel predzadnji korak smijem napraviti jer je \epislon > 0 a -\epsilon < 0??? pa pošto je niz definitivno veći od nule veći je i od \epsilon?
Razumjem da je to više manje namještavanje,ali ako profesor pita što mu reći? S obzirom da on voli takve detalje pitati. Smijem li mu reći da je to namještavanje ili što?
Ako bi mogla pomoć oko jednog zadatka,teorijskog,imam ga rješenog ali mi nisu jasne baš sve stvari,ma kako trivijalne bile. Zadatak je dokazati da je [tex] \sqrt[n]{n} [/tex]
[tex] \epsilon>0 [/tex]
[tex](1+\epsilon)^n = 1 + n*\epsilon + \frac{n(n-1)}{2}\epsilon^2 + .... + \epsilon^n \geq \frac{n(n-1)}{2}\epsilon^2 [/tex]
Sad za početak mi nije jasno zašto smo počeli sa [tex](1+\epsilon)^n[/tex],jel samo zato da se poslije naštima na teorem o sendviču tj omeđenost?
Sad provjeravamo dali je [tex]\frac{n-1}{2}\epsilon^2 > 1 [/tex] Zašto baš to??
[tex]\Rightarrow n>1+\frac{2}{\epsilon^2}[/tex]
Po Arhimedovom aksiomu postoji [tex] n_{0}=n_{0}(\epsilon)\in N[/tex] takav da je [tex]n_{0} > 1+\frac{2}{\epsilon^2}[/tex] tj. [tex]\frac{n_{0}-1}{2}\epsilon^2>1[/tex]
[tex]\Rightarrow n\geq n_{0} \Rightarrow (1+\epsilon)^n \geq n(\frac{n-1}{2})\epsilon^2 \geq n(\frac{n_{0}-1}{2})\epsilon^2 > n > 1[/tex]
[tex] (1+\epsilon)^n > n > 1 [/tex] primjenimo n-ti korjen
[tex](1+\epsilon) > \sqrt[n]{n} > 1 [/tex]
[tex]\epsilon > \sqrt[n]{n} > 0 [/tex]
[tex] \mid \sqrt[n]{n} -1 \mid < \epsilon [/tex]
[tex] \Rightarrow \lim \sqrt[n]{n} = 1 [/tex]
Jel predzadnji korak smijem napraviti jer je \epislon > 0 a -\epsilon < 0??? pa pošto je niz definitivno veći od nule veći je i od \epsilon?
Razumjem da je to više manje namještavanje,ali ako profesor pita što mu reći? S obzirom da on voli takve detalje pitati. Smijem li mu reći da je to namještavanje ili što?
|
|
| [Vrh] |
|
gflegar
Forumaš(ica)


Pridružen/a: 12. 10. 2011. (15:03:41)
Postovi: (10D)16
Spol: 
|
|
| [Vrh] |
|
|













