|
1. funkcija [latex]f : X \rightarrow \mathbb{N} \\ f(x) = -\frac{x-1}{2}[/latex] je očito bijekcija. Pokazati to, ako nije očito :)
2. Ovaj nisam siguran, ali, ovako nekako bi možda to moglo ići. Svaki neprazni podskup dobro uređenog skupa (DUS) ima najmanji element (to je po definiciji). Moje ideja rješenja je ovako nešto. Uzmimo proizvoljan a iz A ([latex](A, \prec)[/latex] je DUS). Sad, definiramo skup [latex]B \subset A, x \in B \leftrightarrow a \prec x[/latex]. Najmanji element ovog skupa je upravo neposredni sljedbenik od a. Mislim da ovo valja, jedino bi trebalo još pokazati da je B neprazan, ali to je OK, jer, pretpostavljam, ovdje je u zadatku u pitanju beskonačan DUS (ako je konačan, onda tvrdnja očito ne vrijedi za najveći element DUS-a)
3. Ravnine u prostoru su dane implicitno jednadžbom [latex]Ax + By + Cz + D = 0[/latex]. Znači, treba odrediti koliko ima takvih jednadžbi. Očito ih je c (npr. injekxija [latex]f : {sve ravnine} \rightarrow $\mathbb{R}$ f (ravnina) = 2^{A}3^{B}5^{C}7^{D}[/latex], injekcija f : \mathbb{R} \rightarrow {sve ravnine} f (A) = Ax [/latex], mislim da ovo valja)
4. Ovdje je injekcija s [0,1> u <2, 4> definirana s 2+x je u redu. Obratno, s <2,4> u [0,1> definirana s 1-x/4 je dobra
[size=9][color=#999999]Added after 4 minutes:[/color][/size]
Nadam se da nisam sfušo ništ ovdje. Ak netko vidi grešku, nek ispravi
1. funkcija 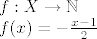 je očito bijekcija. Pokazati to, ako nije očito je očito bijekcija. Pokazati to, ako nije očito 
2. Ovaj nisam siguran, ali, ovako nekako bi možda to moglo ići. Svaki neprazni podskup dobro uređenog skupa (DUS) ima najmanji element (to je po definiciji). Moje ideja rješenja je ovako nešto. Uzmimo proizvoljan a iz A (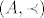 je DUS). Sad, definiramo skup je DUS). Sad, definiramo skup 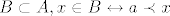 . Najmanji element ovog skupa je upravo neposredni sljedbenik od a. Mislim da ovo valja, jedino bi trebalo još pokazati da je B neprazan, ali to je OK, jer, pretpostavljam, ovdje je u zadatku u pitanju beskonačan DUS (ako je konačan, onda tvrdnja očito ne vrijedi za najveći element DUS-a) . Najmanji element ovog skupa je upravo neposredni sljedbenik od a. Mislim da ovo valja, jedino bi trebalo još pokazati da je B neprazan, ali to je OK, jer, pretpostavljam, ovdje je u zadatku u pitanju beskonačan DUS (ako je konačan, onda tvrdnja očito ne vrijedi za najveći element DUS-a)
3. Ravnine u prostoru su dane implicitno jednadžbom 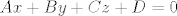 . Znači, treba odrediti koliko ima takvih jednadžbi. Očito ih je c (npr. injekxija . Znači, treba odrediti koliko ima takvih jednadžbi. Očito ih je c (npr. injekxija 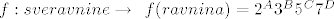 , injekcija f : \mathbb{R} \rightarrow {sve ravnine} f (A) = Ax [/latex], mislim da ovo valja) , injekcija f : \mathbb{R} \rightarrow {sve ravnine} f (A) = Ax [/latex], mislim da ovo valja)
4. Ovdje je injekcija s [0,1> u <2, 4> definirana s 2+x je u redu. Obratno, s <2,4> u [0,1> definirana s 1-x/4 je dobra
Added after 4 minutes:
Nadam se da nisam sfušo ništ ovdje. Ak netko vidi grešku, nek ispravi
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |





