| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Ante_Balota
Forumaš(ica)

Pridružen/a: 16. 07. 2011. (18:53:05)
Postovi: (2)16
|
 Postano: 19:11 sub, 16. 7. 2011 Naslov: zadatak - nadite povrsinu omedenu elipsom Postano: 19:11 sub, 16. 7. 2011 Naslov: zadatak - nadite povrsinu omedenu elipsom |
    |
|
|
pozdrav!
Ovo mi je jedna od zadnjih solucija, ispalija san, nemoguce da nitko nezna rjesit ovaj glupi zadatak.Proba san kod 5 pmf-ovaca...
Ako ko ima volje i zna, bija bi mu vjecno zahvalan, ako ne, samo me ignorirajte. Hvala
Nadite povrsinu omedenu elipsom
(x-5y+3)^2+(3x+4y-1)^2=100
ovako mi je receno da se triba rjesit:
"uvođenjem u i v, dobijem da je u^2+v^2=100 i iz toga da je a^2*b^2=100, korjenujemo i dobijemo da je a*b=10, tj. P=10*pi."
ps.pardon ako san falija podforum :S
pozdrav!
Ovo mi je jedna od zadnjih solucija, ispalija san, nemoguce da nitko nezna rjesit ovaj glupi zadatak.Proba san kod 5 pmf-ovaca...
Ako ko ima volje i zna, bija bi mu vjecno zahvalan, ako ne, samo me ignorirajte. Hvala
Nadite povrsinu omedenu elipsom
(x-5y+3)^2+(3x+4y-1)^2=100
ovako mi je receno da se triba rjesit:
"uvođenjem u i v, dobijem da je u^2+v^2=100 i iz toga da je a^2*b^2=100, korjenujemo i dobijemo da je a*b=10, tj. P=10*pi."
ps.pardon ako san falija podforum :S
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 1:24 ned, 17. 7. 2011 Naslov: Re: zadatak - nadite povrsinu omedenu elipsom Postano: 1:24 ned, 17. 7. 2011 Naslov: Re: zadatak - nadite povrsinu omedenu elipsom |
    |
|
|
[quote="Ante_Balota"]ovako mi je receno da se triba rjesit:
"uvođenjem u i v, dobijem da je u^2+v^2=100 i iz toga da je a^2*b^2=100, korjenujemo i dobijemo da je a*b=10, tj. P=10*pi."[/quote]
Prateći ovu logiku ispalo bi da svaka elipsa oblika [latex]w(x,y)^2+z(x,y)^2=100[/latex] ima površinu [latex]10\pi[/latex] što nije istina.
Svaka elipsa oblika [latex]ax^2+2bxy+cy^2+2dx+2fy+g=0[/latex] može se rotacijom koordinatnog sustava natjerati do oblika koji ne sadrži nelinearan član xy.
Općenito, neka je [latex]b\neq 0[/latex] i neka je [latex]\theta[/latex] kut rotacije koordinatnog sustava. Nove koordinate za x i y biti će:
[latex]x'= x \cos \theta - y \sin \theta,\\
y' = x \sin \theta + y \cos \theta.
[/latex]
Nakon što x' i y' uvrstimo u opću jednadžbu krivulje 2. reda, dobivamo da član uz xy je jednak [latex]2b\cos 2\theta+(c-a)\sin 2\theta[/latex]. Želimo ukloniti xy pa iz toga slijedi da mora biti
[latex]\displaystyle\theta = \frac{1}{2}arccot\frac{a-c}{2b}[/latex],
uz pretpostavku a<c (ako je a>c onda treba dodati još [latex]\frac{\pi}{2}[/latex]). U ovom slučaju, [latex]\theta = -\frac{1}{2}arccot\frac{31}{14}[/latex].
Sada u (x-5y+3)^2+(3x+4y-1)^2=100 umjesto x uvrštavamo [latex]x\cos \theta - y\sin \theta[/latex], a umjesto y uvrštavamo [latex]x\sin \theta + y\cos \theta[/latex]. Nakon nešto sređivanja, elipsa zarotirana za kut [latex]\theta[/latex] imati će jednadžbu
[latex]\left( 51-\sqrt{1157} \right)\left(x-\frac{38 \sin\theta}{51-\sqrt{1157}}\right)^2+
\left( 51+\sqrt{1157} \right)\left(y-\frac{38 \cos\theta}{51+\sqrt{1157}}\right)^2
=200[/latex]
iz čega slijedi da je [latex](ab)^2=\frac{200^2}{1444}[/latex] pa je [latex]ab=\frac{100}{19}[/latex], odnosno, površina je [latex]\frac{100\pi}{19}[/latex]. Jer rotacija čuva površinu, tada je površina elipse s početka zadatka također jednaka [latex]\frac{100\pi}{19}[/latex].
To je bio nešto teži način. Lakši način bi bio upisati u google ellipse, otići na [url=http://mathworld.wolfram.com/Ellipse.html]Wolframovu stranicu o elipsi[/url], pročitati jednadžbe za duljine poluosi (jednadžbe 21 i 22 u http://mathworld.wolfram.com/Ellipse.html) i od tamo izračunati površinu.
| Ante_Balota (napisa): | ovako mi je receno da se triba rjesit:
"uvođenjem u i v, dobijem da je u^2+v^2=100 i iz toga da je a^2*b^2=100, korjenujemo i dobijemo da je a*b=10, tj. P=10*pi." |
Prateći ovu logiku ispalo bi da svaka elipsa oblika 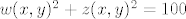 ima površinu ima površinu 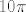 što nije istina. što nije istina.
Svaka elipsa oblika 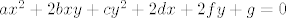 može se rotacijom koordinatnog sustava natjerati do oblika koji ne sadrži nelinearan član xy. može se rotacijom koordinatnog sustava natjerati do oblika koji ne sadrži nelinearan član xy.
Općenito, neka je 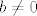 i neka je i neka je 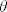 kut rotacije koordinatnog sustava. Nove koordinate za x i y biti će: kut rotacije koordinatnog sustava. Nove koordinate za x i y biti će:
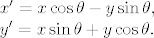
Nakon što x' i y' uvrstimo u opću jednadžbu krivulje 2. reda, dobivamo da član uz xy je jednak 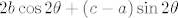 . Želimo ukloniti xy pa iz toga slijedi da mora biti . Želimo ukloniti xy pa iz toga slijedi da mora biti
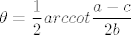 , ,
uz pretpostavku a<c (ako je a>c onda treba dodati još 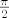 ). U ovom slučaju, ). U ovom slučaju, 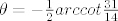 . .
Sada u (x-5y+3)^2+(3x+4y-1)^2=100 umjesto x uvrštavamo  , a umjesto y uvrštavamo , a umjesto y uvrštavamo  . Nakon nešto sređivanja, elipsa zarotirana za kut . Nakon nešto sređivanja, elipsa zarotirana za kut 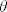 imati će jednadžbu imati će jednadžbu
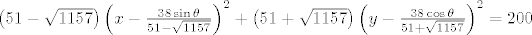
iz čega slijedi da je 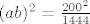 pa je pa je 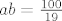 , odnosno, površina je , odnosno, površina je 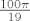 . Jer rotacija čuva površinu, tada je površina elipse s početka zadatka također jednaka . Jer rotacija čuva površinu, tada je površina elipse s početka zadatka također jednaka 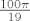 . .
To je bio nešto teži način. Lakši način bi bio upisati u google ellipse, otići na Wolframovu stranicu o elipsi, pročitati jednadžbe za duljine poluosi (jednadžbe 21 i 22 u http://mathworld.wolfram.com/Ellipse.html) i od tamo izračunati površinu.
_________________
The Dude Abides
Zadnja promjena: goranm; 2:24 ned, 17. 7. 2011; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 1:39 ned, 17. 7. 2011 Naslov: Postano: 1:39 ned, 17. 7. 2011 Naslov: |
    |
|
|
Inace, dobar prvi korak je provjeriti sto trebas dobiti. Na primjer, [url=http://www.wolframalpha.com/input/?i=%28x-5y%2B3%29^2%2B%283x%2B4y-1%29^2%3D100]pitas Wolfram|Alphu[/url] i onda tamo piknes "Properties" (desno od "Ellipse" u drugom boxu, onom koji se zove "Geometric figure"), pa odmah vidis da je povrsina priblizno 16.5347 (ovo sto je goranm dobio), sto ti kaze da onih [latex]10\pi[/latex] nije dobro.
Inace, dobar prvi korak je provjeriti sto trebas dobiti. Na primjer, pitas Wolfram|Alphu i onda tamo piknes "Properties" (desno od "Ellipse" u drugom boxu, onom koji se zove "Geometric figure"), pa odmah vidis da je povrsina priblizno 16.5347 (ovo sto je goranm dobio), sto ti kaze da onih 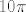 nije dobro. nije dobro.
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Ante_Balota
Forumaš(ica)

Pridružen/a: 16. 07. 2011. (18:53:05)
Postovi: (2)16
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
|
| [Vrh] |
|
|






