| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
boksi
Forumaš(ica)

Pridružen/a: 02. 09. 2011. (16:37:55)
Postovi: (44)16
Spol: 
|
 Postano: 17:10 pet, 30. 9. 2011 Naslov: Re: EM1: zadace 2011./12. Postano: 17:10 pet, 30. 9. 2011 Naslov: Re: EM1: zadace 2011./12. |
    |
|
|
[quote="krcko"]Objavljena je [url=http://web.math.hr/nastava/em/zadace_em1.html]prva domaca zadaca[/url]. Rijesite je, jer ce slicni zadaci biti u drugom kratkom testu![/quote]
možemo li pitanja ovdje?
jer ja imam nekoliko.
3.d.[i] Između svaka dva racionalna broja postoji realan broj [/i] pišemo ∀m,n iz skupa Q ,∃ p iz skupa R za koji m<p<n ili pak m ≤p ≤r
i odrediti istinitost pod 3.d ?
i,da. mi na vježbama nismo ispitivali inkluzije s partitivnim skupovima, ne znam hoćemo li na blicu trebati samo intuitivno odrediti, ili će biti potreban postupak, što li?
Hvala unaprijed.
| krcko (napisa): | | Objavljena je prva domaca zadaca. Rijesite je, jer ce slicni zadaci biti u drugom kratkom testu! |
možemo li pitanja ovdje?
jer ja imam nekoliko.
3.d. Između svaka dva racionalna broja postoji realan broj pišemo ∀m,n iz skupa Q ,∃ p iz skupa R za koji m<p<n ili pak m ≤p ≤r
i odrediti istinitost pod 3.d ?
i,da. mi na vježbama nismo ispitivali inkluzije s partitivnim skupovima, ne znam hoćemo li na blicu trebati samo intuitivno odrediti, ili će biti potreban postupak, što li?
Hvala unaprijed.
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
 Postano: 17:34 pet, 30. 9. 2011 Naslov: Postano: 17:34 pet, 30. 9. 2011 Naslov: |
    |
|
|
Manje vazno je li nejednakost stroga ili ne. Problem je sto ovako napisana formula nije istinita: mozemo npr. uzeti m=1, n=0 (ili bilo koji m>n). Tvrdnja je ipak istinita i takva bi trebala ostati kad ju se zapise simbolima. Npr. ovako:
[latex](\forall m,n\in\mathbb{Q})(\exists p\in\mathbb{R})\, m\le p\le n \lor n\le p\le m[/latex]
Probajte sa strogom nejednakosti i s implikacijom!
Koliko se sjecam partitivni skup se ne pojavljuje u drugom blicu :)
[size=9][color=#999999]Added after 4 minutes:[/color][/size]
:-k
Kad bolje razmislim ovako napisana tvrdnja je glupa jer mozemo uzeti p=m ili p=n. Pametnija je ako se "izmedju" tumaci kao "strogo izmedju". Tocnije, ovako:
[latex](\forall m,n\in\mathbb{Q})\, (m<n \Rightarrow ((\exists p\in\mathbb{R}) m<p<n))[/latex]
Manje vazno je li nejednakost stroga ili ne. Problem je sto ovako napisana formula nije istinita: mozemo npr. uzeti m=1, n=0 (ili bilo koji m>n). Tvrdnja je ipak istinita i takva bi trebala ostati kad ju se zapise simbolima. Npr. ovako:
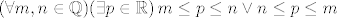
Probajte sa strogom nejednakosti i s implikacijom!
Koliko se sjecam partitivni skup se ne pojavljuje u drugom blicu 
Added after 4 minutes:

Kad bolje razmislim ovako napisana tvrdnja je glupa jer mozemo uzeti p=m ili p=n. Pametnija je ako se "izmedju" tumaci kao "strogo izmedju". Tocnije, ovako:
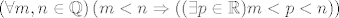
_________________
Vedran Krcadinac
Ljudi su razliciti, a nula je paran broj.
|
|
| [Vrh] |
|
boksi
Forumaš(ica)

Pridružen/a: 02. 09. 2011. (16:37:55)
Postovi: (44)16
Spol: 
|
|
| [Vrh] |
|
Freyja
Forumaš(ica)

Pridružen/a: 30. 09. 2011. (20:54:35)
Postovi: (1)16
|
 Postano: 20:57 pet, 30. 9. 2011 Naslov: Postano: 20:57 pet, 30. 9. 2011 Naslov: |
    |
|
|
[quote="krcko"]
Kad bolje razmislim ovako napisana tvrdnja je glupa jer mozemo uzeti p=m ili p=n. Pametnija je ako se "izmedju" tumaci kao "strogo izmedju". Tocnije, ovako:
[latex](\forall m,n\in\mathbb{Q})\, (m<n \Rightarrow ((\exists p\in\mathbb{R}) m<p<n))[/latex][/quote]
Da li je i ovo točno? (Da li će se priznati ako tako napišem na testu?)
[latex](\forall m,n\in\mathbb{Q}, m<n)\, (\exists p\in\mathbb{R}) m<p<n[/latex]
Ili se mora koristiti ova implikacija kao u Vašem prikazu? Znam da je to "točnije", i tako ću i ja pisati, samo me zanima da li je i ovaj gornji zapis dobar.
| krcko (napisa): |
Kad bolje razmislim ovako napisana tvrdnja je glupa jer mozemo uzeti p=m ili p=n. Pametnija je ako se "izmedju" tumaci kao "strogo izmedju". Tocnije, ovako:
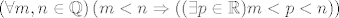 |
Da li je i ovo točno? (Da li će se priznati ako tako napišem na testu?)
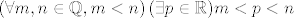
Ili se mora koristiti ova implikacija kao u Vašem prikazu? Znam da je to "točnije", i tako ću i ja pisati, samo me zanima da li je i ovaj gornji zapis dobar.
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
matematičarka
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:19:07)
Postovi: (38)16
Lokacija: Planet Zemlja
|
|
| [Vrh] |
|
banana
Forumaš(ica)

Pridružen/a: 02. 10. 2011. (15:31:28)
Postovi: (8)16
Spol: 
|
|
| [Vrh] |
|
matematičarka
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:19:07)
Postovi: (38)16
Lokacija: Planet Zemlja
|
|
| [Vrh] |
|
anamarie
Forumaš(ica)

Pridružen/a: 07. 09. 2011. (10:59:19)
Postovi: (87)16
Spol: 
|
|
| [Vrh] |
|
Mignon
Forumaš(ica)


Pridružen/a: 12. 09. 2010. (14:05:45)
Postovi: (B6)16
Spol: 
Lokacija: 206
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
StarShooterSupreme
Forumaš(ica)


Pridružen/a: 25. 10. 2011. (17:48:50)
Postovi: (5)16
Spol: 
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
Jurinho
Forumaš(ica)


Pridružen/a: 01. 11. 2011. (23:39:13)
Postovi: (26)16
Spol: 
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
 Postano: 7:07 sri, 30. 11. 2011 Naslov: Postano: 7:07 sri, 30. 11. 2011 Naslov: |
    |
|
|
[quote="krcko"]Gradivo s predavanja i vjezbi su skupovi u opcem polozaju. Presjek je debeli, ali postoje stvari koje se rade samo na vjezbama ili samo na predavanjima. Na kraju je vazno da TI shvatis osnovne pojmove i budes u stanju samostalno rjesavati zadatke. Dakle zasuci mozak, napregni rukave i baci se na zadacu. Nikom se ne svidja kad mora raditi, ali bez toga nema studiranja :P[/quote]
Yes, Sir! Thank you, Sir! Right away, Sir! :)
| krcko (napisa): | Gradivo s predavanja i vjezbi su skupovi u opcem polozaju. Presjek je debeli, ali postoje stvari koje se rade samo na vjezbama ili samo na predavanjima. Na kraju je vazno da TI shvatis osnovne pojmove i budes u stanju samostalno rjesavati zadatke. Dakle zasuci mozak, napregni rukave i baci se na zadacu. Nikom se ne svidja kad mora raditi, ali bez toga nema studiranja  |
Yes, Sir! Thank you, Sir! Right away, Sir! 
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
|











