| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Saf
Forumski umjetnik


Pridružen/a: 10. 06. 2005. (21:55:28)
Postovi: (1B0)16
Spol: 
Lokacija: Zagreb
|
 Postano: 23:33 uto, 4. 10. 2011 Naslov: Izračun štednje i politika banaka Postano: 23:33 uto, 4. 10. 2011 Naslov: Izračun štednje i politika banaka |
    |
|
|
Pokušavam napraviti kalkulator za izračun štednje, muči me par sitnica, radi se o složenom kamatnom računu... Zapravo me muči koja je praksa i koja se formula primjenjuje u bankarstvu kada se godišnja kamatna stopa primjenjuje na štednje kraće od 1 godine.
Slučaj 1.
Oročena štednja, kamatna stopa godišnja, rok oročenja 3 mjeseca. Primjera radi, [latex]G[/latex]-lavnica=100, [latex]k[/latex]-amatnjak=0.1 (10%), [latex]m[/latex]-jeseci=3:
a) [latex]G * (1+k)^{m/12} =>100 * (1+0.10)^{3/12} = 102.41[/latex]
b) [latex]G * (1 + k*m/12) => 100 * (1 + 0.1*3/12) = 102.5[/latex]
c) [latex]G * (1 + k/12)^{{(m/12)}*12} => 100 * (1 + 0.10/12)^3 = 102.52[/latex] (znači li ovo da se kamata zapravo obračunava mjesečno a ne godišnje)
Koju praksu imaju banke, koju formulu koriste? b) i c) mi se čine nekako najmanje vjerojatnom jer više odgovaraju štediši, iako mi se čini da se kolokvijalno koristi upravo b) za procjenu ušteđenog iznosa. Ovisi li od banke do banke ili postoji generalno pravilo.
Slučaj 2.
Tu me sad muči formula... Riječ je o "aktivnoj" štednji sa mjesečnim uplatama. Ako su sve uplate istog iznosa, odnosno ako je štednja obročna (npr stambena štedionica...), znam formulu, međutim ne mogu pronaći/izvest formulu za "aktivnu" štednju kada se na glavnicu mjesečno uplaćuju isti iznosi (različiti od glavnice). Npr
[quote]1000 kn na 7 mjeseci uz godišnju kamatu od 5% i uz mjesečne uplate od 100 kn...
[/quote]
Dakle kako se ovo da je glavnica svaki slijedeći mjesec narasla i za uplatu od 100 kn ukomponira u godišnju kamatu na rokove kraće od godine...
Molim ekipu sa financijske mi malo to objasni...
Pokušavam napraviti kalkulator za izračun štednje, muči me par sitnica, radi se o složenom kamatnom računu... Zapravo me muči koja je praksa i koja se formula primjenjuje u bankarstvu kada se godišnja kamatna stopa primjenjuje na štednje kraće od 1 godine.
Slučaj 1.
Oročena štednja, kamatna stopa godišnja, rok oročenja 3 mjeseca. Primjera radi, 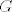 -lavnica=100, -lavnica=100,  -amatnjak=0.1 (10%), -amatnjak=0.1 (10%),  -jeseci=3: -jeseci=3:
a) 
b) 
c) 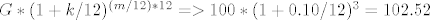 (znači li ovo da se kamata zapravo obračunava mjesečno a ne godišnje) (znači li ovo da se kamata zapravo obračunava mjesečno a ne godišnje)
Koju praksu imaju banke, koju formulu koriste? b) i c) mi se čine nekako najmanje vjerojatnom jer više odgovaraju štediši, iako mi se čini da se kolokvijalno koristi upravo b) za procjenu ušteđenog iznosa. Ovisi li od banke do banke ili postoji generalno pravilo.
Slučaj 2.
Tu me sad muči formula... Riječ je o "aktivnoj" štednji sa mjesečnim uplatama. Ako su sve uplate istog iznosa, odnosno ako je štednja obročna (npr stambena štedionica...), znam formulu, međutim ne mogu pronaći/izvest formulu za "aktivnu" štednju kada se na glavnicu mjesečno uplaćuju isti iznosi (različiti od glavnice). Npr
| Citat: | 1000 kn na 7 mjeseci uz godišnju kamatu od 5% i uz mjesečne uplate od 100 kn...
|
Dakle kako se ovo da je glavnica svaki slijedeći mjesec narasla i za uplatu od 100 kn ukomponira u godišnju kamatu na rokove kraće od godine...
Molim ekipu sa financijske mi malo to objasni...
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
|
| [Vrh] |
|
Saf
Forumski umjetnik


Pridružen/a: 10. 06. 2005. (21:55:28)
Postovi: (1B0)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
 Postano: 13:07 pet, 7. 10. 2011 Naslov: Postano: 13:07 pet, 7. 10. 2011 Naslov: |
    |
|
|
(a) bi imalo smisla kad bi stopa k imala drukčiju interpretaciju. Naime, primijeti da stopa k [b]nije[/b] takva da nakon godinu dana imaš [tex]G(1+k)[/tex] kuna. Stopa k je nominalna godišnja kamatna stopa i njena interpretacija je točno takva da vrijedi (b) ili (c) (ovisno o razdoblju obračuna). Uobičajeno se pod godišnjom kamatnom stopom podrazumijeva nominalna godišnja kamatna stopa.
S druge strane, postoji efektivna godišnja kamatna stopa. Recimo da se kamata obračunava mjesečno. Tada nakon godinu dana imaš [tex]G(1+k/12)^{12}[/tex] kn. Efektivna godišnja kamatna stopa k' je takva da vrijedi:
[dtex]G(1+k')=G(1+k/12)^{12}[/dtex]
Drugim riječima, [tex]k'=(1+k/12)^{12}-1\approx 10.47\%[/tex]. E, k' je stopa za koju nakon godinu dana imaš [tex]G(1+k')[/tex] kn i za nju vrijedi (a).
Nominalna kamatna stopa dobije pravi smisao kad prijeđeš na kontinuirano ukamaćivanje. Pretpostavimo da perioda ukamaćivanja u godini ima n. Tada je efektivna kamatna stopa [tex]k'_n=(1+k/n)^n-1[/tex]. Prelaskom na limes imamo:
[dtex]k'=\lim_n k'_n=e^k-1[/dtex]
Drugim riječima, nakon godinu dana imaš [tex]Ge^k[/tex] kn.
A što se tiče ovoga o isplativosti, u konačnici je ionako banka ta koja određuje k, tako da je njoj uvijek isplativo.
(a) bi imalo smisla kad bi stopa k imala drukčiju interpretaciju. Naime, primijeti da stopa k nije takva da nakon godinu dana imaš [tex]G(1+k)[/tex] kuna. Stopa k je nominalna godišnja kamatna stopa i njena interpretacija je točno takva da vrijedi (b) ili (c) (ovisno o razdoblju obračuna). Uobičajeno se pod godišnjom kamatnom stopom podrazumijeva nominalna godišnja kamatna stopa.
S druge strane, postoji efektivna godišnja kamatna stopa. Recimo da se kamata obračunava mjesečno. Tada nakon godinu dana imaš [tex]G(1+k/12)^{12}[/tex] kn. Efektivna godišnja kamatna stopa k' je takva da vrijedi:
[dtex]G(1+k')=G(1+k/12)^{12}[/dtex]
Drugim riječima, [tex]k'=(1+k/12)^{12}-1\approx 10.47\%[/tex]. E, k' je stopa za koju nakon godinu dana imaš [tex]G(1+k')[/tex] kn i za nju vrijedi (a).
Nominalna kamatna stopa dobije pravi smisao kad prijeđeš na kontinuirano ukamaćivanje. Pretpostavimo da perioda ukamaćivanja u godini ima n. Tada je efektivna kamatna stopa [tex]k'_n=(1+k/n)^n-1[/tex]. Prelaskom na limes imamo:
[dtex]k'=\lim_n k'_n=e^k-1[/dtex]
Drugim riječima, nakon godinu dana imaš [tex]Ge^k[/tex] kn.
A što se tiče ovoga o isplativosti, u konačnici je ionako banka ta koja određuje k, tako da je njoj uvijek isplativo.
_________________
I don't know half of you half as well as I should like; and I like less than half of you half as well as you deserve.
|
|
| [Vrh] |
|
Saf
Forumski umjetnik


Pridružen/a: 10. 06. 2005. (21:55:28)
Postovi: (1B0)16
Spol: 
Lokacija: Zagreb
|
 Postano: 19:06 pet, 7. 10. 2011 Naslov: Postano: 19:06 pet, 7. 10. 2011 Naslov: |
    |
|
|
[quote]Drugim riječima, k′=(1+k/12)12−1≈10.47%. E, k' je stopa za koju nakon godinu dana imaš G(1+k′) kn i za nju vrijedi (a). [/quote]
Hvala, ovo mi je falilo...
Znači, kada bi htio napraviti kalkulator za štednju koristeći godišnju efektivnu kamatnu stopu koja se obračunava mjesečno i mogučnost mjesečnih uplata (postnumerando) trebao bi koristiti slijedeću formulu:
[latex]G * (1+\frac{k}{12})^\frac{n}{12} + y * (1+\frac{k}{12})^\frac{n-1}{12} +...+ y*(1+\frac{k}{12}) + y[/latex]
gdje je G = glavnica, k = EKS, n = mjeseci, y = mjesečna uplata?
Neovisno o kojoj banci je riječ, hoće li to dati dovoljno precizan rezultat?
| Citat: | | Drugim riječima, k′=(1+k/12)12−1≈10.47%. E, k' je stopa za koju nakon godinu dana imaš G(1+k′) kn i za nju vrijedi (a). |
Hvala, ovo mi je falilo...
Znači, kada bi htio napraviti kalkulator za štednju koristeći godišnju efektivnu kamatnu stopu koja se obračunava mjesečno i mogučnost mjesečnih uplata (postnumerando) trebao bi koristiti slijedeću formulu:
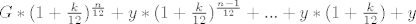
gdje je G = glavnica, k = EKS, n = mjeseci, y = mjesečna uplata?
Neovisno o kojoj banci je riječ, hoće li to dati dovoljno precizan rezultat?
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
 Postano: 8:08 sub, 8. 10. 2011 Naslov: Postano: 8:08 sub, 8. 10. 2011 Naslov: |
    |
|
|
Ako je k efektivna godišnja kamatna stopa, formula je sljedeća (usporedi s (a)):
[dtex]G(1+k)^{n/12}+y(1+k)^{(n-1)/12}+\ldots+y(1+k)+y\,.[/dtex]
Ako je k nominalna godišnja kamatna stopa, formula je sljedeća (usporedi s (c)):
[dtex]G(1+k/12)^n+y(1+k/12)^{n-1}+\ldots+y(1+k/12)+y\,.[/dtex]
Banka će ti najvjerojatnije dati nominalnu godišnju kamatnu stopu.
Btw, nisam siguran oko terminologije. Kad sam ja čitao o ovome, koristio sam literaturu na engleskom (pogledaj npr. http://en.wikipedia.org/wiki/Nominal_interest_rate i http://en.wikipedia.org/wiki/Effective_interest_rate). Čini mi se da se kod nas pojmovi nominalna i efektivna kamatna stopa koriste za nešto drugo kad je riječ o kreditima. Nana, možda ti znaš?
Ako je k efektivna godišnja kamatna stopa, formula je sljedeća (usporedi s (a)):
[dtex]G(1+k)^{n/12}+y(1+k)^{(n-1)/12}+\ldots+y(1+k)+y\,.[/dtex]
Ako je k nominalna godišnja kamatna stopa, formula je sljedeća (usporedi s (c)):
[dtex]G(1+k/12)^n+y(1+k/12)^{n-1}+\ldots+y(1+k/12)+y\,.[/dtex]
Banka će ti najvjerojatnije dati nominalnu godišnju kamatnu stopu.
Btw, nisam siguran oko terminologije. Kad sam ja čitao o ovome, koristio sam literaturu na engleskom (pogledaj npr. http://en.wikipedia.org/wiki/Nominal_interest_rate i http://en.wikipedia.org/wiki/Effective_interest_rate). Čini mi se da se kod nas pojmovi nominalna i efektivna kamatna stopa koriste za nešto drugo kad je riječ o kreditima. Nana, možda ti znaš?
_________________
I don't know half of you half as well as I should like; and I like less than half of you half as well as you deserve.
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
|
| [Vrh] |
|
nana
Forumaš(ica)


Pridružen/a: 29. 11. 2005. (12:24:35)
Postovi: (2AD)16
Spol: 
|
 Postano: 14:21 sub, 8. 10. 2011 Naslov: Postano: 14:21 sub, 8. 10. 2011 Naslov: |
    |
|
|
Da, ja isto imam PBZ. I vidim svako malo je neki obracun kamata od max 20lipa.
[quote="PBZ"]Kamata
(*) na sredstva na tekućem računu obračunava se kamata po kamatnoj stopi u visini 0,10% godišnje, promjenjivo[/quote]
Meni opet nije bas jasno na sto tocno obracunaju
Znaci zadnji dan u mjesecu je pripis kamate. Ako je 0,1% godisnje onda bi tebalo biti 0,1/12% al meni nije tako :D zapravo računala sam si koliki dio od trenutnog (na dan pripisa) je kamata i svaki put drukčije. Tako da..... :D 8)
Da, ja isto imam PBZ. I vidim svako malo je neki obracun kamata od max 20lipa.
| PBZ (napisa): | Kamata
(*) na sredstva na tekućem računu obračunava se kamata po kamatnoj stopi u visini 0,10% godišnje, promjenjivo |
Meni opet nije bas jasno na sto tocno obracunaju
Znaci zadnji dan u mjesecu je pripis kamate. Ako je 0,1% godisnje onda bi tebalo biti 0,1/12% al meni nije tako  zapravo računala sam si koliki dio od trenutnog (na dan pripisa) je kamata i svaki put drukčije. Tako da..... zapravo računala sam si koliki dio od trenutnog (na dan pripisa) je kamata i svaki put drukčije. Tako da.....  
_________________ Kad sam bila mala htjela sam biti statističarka 
[tex]\omega \in \Omega[/tex]  |
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
|
| [Vrh] |
|
Saf
Forumski umjetnik


Pridružen/a: 10. 06. 2005. (21:55:28)
Postovi: (1B0)16
Spol: 
Lokacija: Zagreb
|
 Postano: 18:04 sub, 8. 10. 2011 Naslov: Postano: 18:04 sub, 8. 10. 2011 Naslov: |
    |
|
|
[quote="Melkor"][dtex]y(1+k)^{(n-1)/12}+\ldots+y(1+k)+y\,.[/dtex]
[/quote]
Jel bi ovo bila formula za sumu ovog reda (malo sam zahrđao):
[latex]y*\frac{1 - (1+k)^\frac{(n-1)}{12}}{k}[/latex]
Odnosno lijepa formula (bez velike kobasice od sume) bi bila:
[latex]G*(1+k)^\frac{n}{12} + y*\frac{1 - (1+k)^\frac{(n-1)}{12}}{k}[/latex]
Gdje je G glavnica, y je mjesečna uplata, k je EKS, n je period u mjesecima...
Nije za komercijalne potrebe, ali bih volio ponuditi userima korisni štedni kalkulator na portalu za osobne financije na kojem radim...
| Melkor (napisa): | [dtex]y(1+k)^{(n-1)/12}+\ldots+y(1+k)+y\,.[/dtex]
|
Jel bi ovo bila formula za sumu ovog reda (malo sam zahrđao):
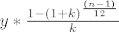
Odnosno lijepa formula (bez velike kobasice od sume) bi bila:

Gdje je G glavnica, y je mjesečna uplata, k je EKS, n je period u mjesecima...
Nije za komercijalne potrebe, ali bih volio ponuditi userima korisni štedni kalkulator na portalu za osobne financije na kojem radim...
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
|
| [Vrh] |
|
Saf
Forumski umjetnik


Pridružen/a: 10. 06. 2005. (21:55:28)
Postovi: (1B0)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
|
| [Vrh] |
|
Saf
Forumski umjetnik


Pridružen/a: 10. 06. 2005. (21:55:28)
Postovi: (1B0)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Saf
Forumski umjetnik


Pridružen/a: 10. 06. 2005. (21:55:28)
Postovi: (1B0)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Saf
Forumski umjetnik


Pridružen/a: 10. 06. 2005. (21:55:28)
Postovi: (1B0)16
Spol: 
Lokacija: Zagreb
|
 Postano: 20:00 sri, 28. 3. 2012 Naslov: Postano: 20:00 sri, 28. 3. 2012 Naslov: |
    |
|
|
[quote="Melkor"]Nope, sve skupa se svede na:
[dtex]G(1+k)^{n/12}+y\frac{1-(1+k)^{n/12}}{1-(1+k)^{1/12}}\,.[/dtex][/quote]
Nameće mi se novi problem, naime, postoje dvije vrste otplate kredita, anuitetska i u ratama.
Razlika je što je kod anuiteta udio glavnice + kamate = const.
Kod otplate u ratama, uvijek se vraća isti iznos (udio) glavnice, a kamata je različita.
E sad, pretpostavljam da gornja formula računa anuitet, koju formulu koristiti za izračun mjesečnog plana otplate u ratama?
| Melkor (napisa): | Nope, sve skupa se svede na:
[dtex]G(1+k)^{n/12}+y\frac{1-(1+k)^{n/12}}{1-(1+k)^{1/12}}\,.[/dtex] |
Nameće mi se novi problem, naime, postoje dvije vrste otplate kredita, anuitetska i u ratama.
Razlika je što je kod anuiteta udio glavnice + kamate = const.
Kod otplate u ratama, uvijek se vraća isti iznos (udio) glavnice, a kamata je različita.
E sad, pretpostavljam da gornja formula računa anuitet, koju formulu koristiti za izračun mjesečnog plana otplate u ratama?
|
|
| [Vrh] |
|
|






















