| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
student_92
Forumaš(ica)

Pridružen/a: 17. 09. 2011. (16:31:46)
Postovi: (B9)16
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 18:12 ned, 2. 10. 2011 Naslov: Re: DZ iz MA1 Postano: 18:12 ned, 2. 10. 2011 Naslov: Re: DZ iz MA1 |
    |
|
|
1. S obzirom da se u nejednadžbi pojavljuje samo [tex]sin[/tex] i [tex]cos[/tex], predacimo [tex]cos[/tex] na lijevu stranu nejednakosti i pretvorimo ga u [tex]sin[/tex] - dakle, on je sada [tex]sin(\frac{\pi}{2}- \pi \sqrt{x})[/tex]. Razliku sinusa znamo po formulama i dobivamo nejednadžbu: [tex]cos(\frac{\pi}{4}+\frac{\pi}{2}(x-\sqrt{x}))sin(-\frac{\pi}{4}+\frac{\pi}{2}(x+\sqrt{x}))>0[/tex], koju je sada lakše razmatrati - ovisno o tome kada je i sinus i kosinus veće od nule, odnosno kada su oba manja od nule. Dalje je malo problematično zbog korijena i otvorenih intervala, pa ću pokazati samo na primjeru sljedećega kako bi to otprilike išlo (upotpuni ostale slučajeve, pa ako bude problema, javi):
[tex]cos(\frac{\pi}{4}+\frac{\pi}{2}(x-\sqrt{x}))>0[/tex]
[tex]-\frac{\pi}{2}+2k\pi<\frac{\pi}{4}+\frac{\pi}{2}(x-\sqrt{x})<\frac{\pi}{2}+2k\pi, k \in \mathbb{Z}[/tex]
[tex]-\frac{3}{2}+4k<x-\sqrt{x}<\frac{1}{2}+4k[/tex]
[tex]-\frac{5}{4}+4k<x-\sqrt{x}+\frac{1}{4}<\frac{3}{4}+4k[/tex]
[tex]-\frac{5}{4}+4k<(\sqrt{x}-\frac{1}{2})^2<\frac{3}{4}+4k[/tex]
I sada tu idu dva slučaja:
[tex]\sqrt{-\frac{5}{4}+4k}<\sqrt{x}-\frac{1}{2}<\sqrt{\frac{3}{4}+4k}, k \in \mathbb{N}[/tex]
[tex]-\sqrt{-\frac{5}{4}+4k}>\sqrt{x}-\frac{1}{2}>-\sqrt{\frac{3}{4}+4k}, k \in \mathbb{N}[/tex]
([tex]k \in \mathbb{N}[/tex] zato što izraz pod korijenom mora biti pozitivan. Dva su slučaja jer izraz ispod kvadrirane zagrade može biti i pozitivan i negativan.)
I da, sad kad pogledamo početak zadatka, trebalo bi raspisati dva slučaja ovisno o predznaku sinusa i kosinusa, znači puno petljanja s ovim korijenima i sličnom. Trenutno ne vidim ljepše rješenje, ali bar nešto...
2. Ovaj ćeš vjerojatno bolje shvatiti. Kratak je pa ću ga sa smjernicama riješiti (i možda ti bude jasno što sam radio u gornjem zadatku jer se ideja ponavlja).
[tex]sin(2 \pi cos(x))>0[/tex]
Pogledaš brojevnu kružnicu i vidiš kada je sinus pozitivan. Zaključuješ:
[tex]2k \pi < 2 \pi cos(x) < \pi + 2k \pi, k \in \mathbb{Z}[/tex]
[tex]k < cos(x) < \frac{1}{2} + k[/tex]
Još se prisjeti da je [tex]-1 \leq cos(x) \leq 1, \forall x \in \mathbb{R}[/tex], pa gore uvrštavaš cijele brojeve [tex]k[/tex] za koje nejednakost ima smisla. Ako uočiš da su traženi brojevi [tex]k = -1, 0[/tex], imaš sljedeće nejednadžbe:
[tex]-1 < cos(x) < \frac{1}{2} -1 = -\frac{1}{2}[/tex]
[tex]0 < cos(x) < \frac{1}{2} + 0 = \frac{1}{2}[/tex]
Sada je jednostavnije. ;)
Nadam se da je od pomoći. Rješenje je čisto preko natuknica pa nije baš najbolje napisano (jer sam mislio da ti trebaju samo natuknice). Pitaj ako nije jasno i probat ću bolje. :)
1. S obzirom da se u nejednadžbi pojavljuje samo [tex]sin[/tex] i [tex]cos[/tex], predacimo [tex]cos[/tex] na lijevu stranu nejednakosti i pretvorimo ga u [tex]sin[/tex] - dakle, on je sada [tex]sin(\frac{\pi}{2}- \pi \sqrt{x})[/tex]. Razliku sinusa znamo po formulama i dobivamo nejednadžbu: [tex]cos(\frac{\pi}{4}+\frac{\pi}{2}(x-\sqrt{x}))sin(-\frac{\pi}{4}+\frac{\pi}{2}(x+\sqrt{x}))>0[/tex], koju je sada lakše razmatrati - ovisno o tome kada je i sinus i kosinus veće od nule, odnosno kada su oba manja od nule. Dalje je malo problematično zbog korijena i otvorenih intervala, pa ću pokazati samo na primjeru sljedećega kako bi to otprilike išlo (upotpuni ostale slučajeve, pa ako bude problema, javi):
[tex]cos(\frac{\pi}{4}+\frac{\pi}{2}(x-\sqrt{x}))>0[/tex]
[tex]-\frac{\pi}{2}+2k\pi<\frac{\pi}{4}+\frac{\pi}{2}(x-\sqrt{x})<\frac{\pi}{2}+2k\pi, k \in \mathbb{Z}[/tex]
[tex]-\frac{3}{2}+4k<x-\sqrt{x}<\frac{1}{2}+4k[/tex]
[tex]-\frac{5}{4}+4k<x-\sqrt{x}+\frac{1}{4}<\frac{3}{4}+4k[/tex]
[tex]-\frac{5}{4}+4k<(\sqrt{x}-\frac{1}{2})^2<\frac{3}{4}+4k[/tex]
I sada tu idu dva slučaja:
[tex]\sqrt{-\frac{5}{4}+4k}<\sqrt{x}-\frac{1}{2}<\sqrt{\frac{3}{4}+4k}, k \in \mathbb{N}[/tex]
[tex]-\sqrt{-\frac{5}{4}+4k}>\sqrt{x}-\frac{1}{2}>-\sqrt{\frac{3}{4}+4k}, k \in \mathbb{N}[/tex]
([tex]k \in \mathbb{N}[/tex] zato što izraz pod korijenom mora biti pozitivan. Dva su slučaja jer izraz ispod kvadrirane zagrade može biti i pozitivan i negativan.)
I da, sad kad pogledamo početak zadatka, trebalo bi raspisati dva slučaja ovisno o predznaku sinusa i kosinusa, znači puno petljanja s ovim korijenima i sličnom. Trenutno ne vidim ljepše rješenje, ali bar nešto...
2. Ovaj ćeš vjerojatno bolje shvatiti. Kratak je pa ću ga sa smjernicama riješiti (i možda ti bude jasno što sam radio u gornjem zadatku jer se ideja ponavlja).
[tex]sin(2 \pi cos(x))>0[/tex]
Pogledaš brojevnu kružnicu i vidiš kada je sinus pozitivan. Zaključuješ:
[tex]2k \pi < 2 \pi cos(x) < \pi + 2k \pi, k \in \mathbb{Z}[/tex]
[tex]k < cos(x) < \frac{1}{2} + k[/tex]
Još se prisjeti da je [tex]-1 \leq cos(x) \leq 1, \forall x \in \mathbb{R}[/tex], pa gore uvrštavaš cijele brojeve [tex]k[/tex] za koje nejednakost ima smisla. Ako uočiš da su traženi brojevi [tex]k = -1, 0[/tex], imaš sljedeće nejednadžbe:
[tex]-1 < cos(x) < \frac{1}{2} -1 = -\frac{1}{2}[/tex]
[tex]0 < cos(x) < \frac{1}{2} + 0 = \frac{1}{2}[/tex]
Sada je jednostavnije. 
Nadam se da je od pomoći. Rješenje je čisto preko natuknica pa nije baš najbolje napisano (jer sam mislio da ti trebaju samo natuknice). Pitaj ako nije jasno i probat ću bolje. 
|
|
| [Vrh] |
|
student_92
Forumaš(ica)

Pridružen/a: 17. 09. 2011. (16:31:46)
Postovi: (B9)16
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 0:26 pon, 3. 10. 2011 Naslov: Re: DZ iz MA1 Postano: 0:26 pon, 3. 10. 2011 Naslov: Re: DZ iz MA1 |
    |
|
|
[quote="student_92"]Hvala puno. Mogu li te još nešto pitati ako mi ne bude bilo jasno? Trudim se uhvatiti korak s gradivom pa mi je trenutno iznad glave nekoliko upitnika.[/quote]
Naravno. Na forumu uvijek ima aktivnih ljudi dobre volje, bilo studenata koji trenutno polažu isti kolegij, bilo demonstratora, a ponekad čak i asistenata i profesora! :)
U svakom slučaju, osjećaj se slobodnim pitati pitanje kad god zapneš. Nemaš što izgubiti, jedino ćeš možda bolje shvatiti gradivo. :D
| student_92 (napisa): | | Hvala puno. Mogu li te još nešto pitati ako mi ne bude bilo jasno? Trudim se uhvatiti korak s gradivom pa mi je trenutno iznad glave nekoliko upitnika. |
Naravno. Na forumu uvijek ima aktivnih ljudi dobre volje, bilo studenata koji trenutno polažu isti kolegij, bilo demonstratora, a ponekad čak i asistenata i profesora! 
U svakom slučaju, osjećaj se slobodnim pitati pitanje kad god zapneš. Nemaš što izgubiti, jedino ćeš možda bolje shvatiti gradivo. 
|
|
| [Vrh] |
|
student_92
Forumaš(ica)

Pridružen/a: 17. 09. 2011. (16:31:46)
Postovi: (B9)16
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
|
| [Vrh] |
|
student_92
Forumaš(ica)

Pridružen/a: 17. 09. 2011. (16:31:46)
Postovi: (B9)16
|
|
| [Vrh] |
|
boksi
Forumaš(ica)

Pridružen/a: 02. 09. 2011. (16:37:55)
Postovi: (44)16
Spol: 
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
 Postano: 23:15 uto, 4. 10. 2011 Naslov: Postano: 23:15 uto, 4. 10. 2011 Naslov: |
    |
|
|
[quote="boksi"][dtex]Neka je f(x) = |x^2 + 6x + 8| − |x^2 + 4x + 3|. Odredite f(<−2, 2>) i
f^−1(<1, 2]).[/dtex]
trebam se prvo riješiti apsolutnog pa raspisivati po slučajevima ili što?
:?[/quote]
da, rastavi to na par slučaja, [b]mislim[/b] da dobiješ 3 skupa na kojima se funkcija 'mjenja'
1. [latex]x \in <-\infty, -4\] \cup \[-1, +\infty>[/latex]
[b]2.[/b] [latex]x \in < -4, -3] \cup [ -2, -1 >[/latex]
3. [latex]x \in <-3, -2>[/latex]
treba to [b]provjerit...[/b]( posebno ovaj drugi slučaj ) ak nemaš rješenja za takve tipove zadatka, preporučio bi [url=http://math.exeter.edu/rparris/winplot.html]winplot[/url], mali programčić za crtanje ovih osnovnih funkcija na kojima lagano provjeriš otprilike kakvo bi ti rješenje trebalo biti, ili naravno: [url=http://www.wolframalpha.com/input/?i=|x^2%2B6*x%2B8|-|x^2%2B4x%2B3|]wolfram[/url]
:D
| boksi (napisa): | [dtex]Neka je f(x) = |x^2 + 6x + 8| − |x^2 + 4x + 3|. Odredite f(<−2, 2>) i
f^−1(<1, 2]).[/dtex]
trebam se prvo riješiti apsolutnog pa raspisivati po slučajevima ili što?
 |
da, rastavi to na par slučaja, mislim da dobiješ 3 skupa na kojima se funkcija 'mjenja'
1. 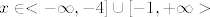
2. 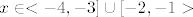
3. 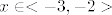
treba to provjerit...( posebno ovaj drugi slučaj ) ak nemaš rješenja za takve tipove zadatka, preporučio bi winplot, mali programčić za crtanje ovih osnovnih funkcija na kojima lagano provjeriš otprilike kakvo bi ti rješenje trebalo biti, ili naravno: wolfram

|
|
| [Vrh] |
|
jema
Forumaš(ica)

Pridružen/a: 29. 09. 2011. (15:56:35)
Postovi: (52)16
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 18:14 sri, 5. 10. 2011 Naslov: Postano: 18:14 sri, 5. 10. 2011 Naslov: |
    |
|
|
[quote="jema"]u kojoj sobi su demonstrature i moze netko napisat njihove mailove da im se javimo prije dolaska jer uvijek prof. kaze da se najavimo kako demosi ne bi bezveze cekali, a nitko ne dođe :) hvala :)[/quote]
Nema neke prostorije u kojoj se stalno drže demonstrature osim ako netko od demonstratora za svoj termin nađe predavaonicu koja je tada prazna. Ali ni to nije garancija jer ju nije rezervirao za sebe. :D
U svakom slučaju, poželjno je najaviti se na mail da demos može očekivati da će netko doći, a i da može računati otprilike koliko bi mu ljudi moglo doći na demonstrature. Ako ti baš ne odgovara zadani termin (znači, sastajanje od sata koji je napisan na webu i na ovom forumu + 15 minuta čekanja), probaj s demosom dogovoriti ako možeš doći malo kasnije tijekom ta dva sata ili ako bi htio/htjela doći neki drugi dan ili sat. Ljudi smo, možemo se valjda nekako dogovoriti! :D
| jema (napisa): | u kojoj sobi su demonstrature i moze netko napisat njihove mailove da im se javimo prije dolaska jer uvijek prof. kaze da se najavimo kako demosi ne bi bezveze cekali, a nitko ne dođe  hvala hvala  |
Nema neke prostorije u kojoj se stalno drže demonstrature osim ako netko od demonstratora za svoj termin nađe predavaonicu koja je tada prazna. Ali ni to nije garancija jer ju nije rezervirao za sebe. 
U svakom slučaju, poželjno je najaviti se na mail da demos može očekivati da će netko doći, a i da može računati otprilike koliko bi mu ljudi moglo doći na demonstrature. Ako ti baš ne odgovara zadani termin (znači, sastajanje od sata koji je napisan na webu i na ovom forumu + 15 minuta čekanja), probaj s demosom dogovoriti ako možeš doći malo kasnije tijekom ta dva sata ili ako bi htio/htjela doći neki drugi dan ili sat. Ljudi smo, možemo se valjda nekako dogovoriti! 
|
|
| [Vrh] |
|
boksi
Forumaš(ica)

Pridružen/a: 02. 09. 2011. (16:37:55)
Postovi: (44)16
Spol: 
|
 Postano: 18:46 uto, 11. 10. 2011 Naslov: Postano: 18:46 uto, 11. 10. 2011 Naslov: |
    |
|
|
hm, imam malo blesavo pitanje, ali kažu da nema glupih pitanja, pa neka:
dakle, slika od [latex](x+1) / (2*x + 3)[/latex] na intervalu od nula do plus beskonačno?
ide od 1/3 do?
ne znam trebam li staviti do beskonačno ili ide 1/2 jer mu limes ide tamo :?
mislim da ću ipak pokušati s 1/2, ali pitat ću prvo ovdje.
hm, imam malo blesavo pitanje, ali kažu da nema glupih pitanja, pa neka:
dakle, slika od 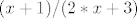 na intervalu od nula do plus beskonačno? na intervalu od nula do plus beskonačno?
ide od 1/3 do?
ne znam trebam li staviti do beskonačno ili ide 1/2 jer mu limes ide tamo 
mislim da ću ipak pokušati s 1/2, ali pitat ću prvo ovdje.
|
|
| [Vrh] |
|
R2-D2
Forumaš(ica)

Pridružen/a: 11. 10. 2011. (20:32:10)
Postovi: (2F)16
|
 Postano: 21:01 uto, 11. 10. 2011 Naslov: Postano: 21:01 uto, 11. 10. 2011 Naslov: |
    |
|
|
[quote="boksi"]hm, imam malo blesavo pitanje, ali kažu da nema glupih pitanja, pa neka:
dakle, slika od [latex](x+1) / (2*x + 3)[/latex] na intervalu od nula do plus beskonačno?
ide od 1/3 do?
ne znam trebam li staviti do beskonačno ili ide 1/2 jer mu limes ide tamo :?
mislim da ću ipak pokušati s 1/2, ali pitat ću prvo ovdje.[/quote]
Nikada ti neće prijeći 1/2. Ali najlakše ti je to iz grafa vidjeti. Malo si središ funkciju i dobiješ 1/2 - 1/(4(x+3/2)). Znači, graf ti ima oblik slično kao -1/x, osim kaj je translatiran za 3/2 ulijevo i za 1/2 u gore.
| boksi (napisa): | hm, imam malo blesavo pitanje, ali kažu da nema glupih pitanja, pa neka:
dakle, slika od 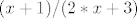 na intervalu od nula do plus beskonačno? na intervalu od nula do plus beskonačno?
ide od 1/3 do?
ne znam trebam li staviti do beskonačno ili ide 1/2 jer mu limes ide tamo 
mislim da ću ipak pokušati s 1/2, ali pitat ću prvo ovdje. |
Nikada ti neće prijeći 1/2. Ali najlakše ti je to iz grafa vidjeti. Malo si središ funkciju i dobiješ 1/2 - 1/(4(x+3/2)). Znači, graf ti ima oblik slično kao -1/x, osim kaj je translatiran za 3/2 ulijevo i za 1/2 u gore.
|
|
| [Vrh] |
|
boksi
Forumaš(ica)

Pridružen/a: 02. 09. 2011. (16:37:55)
Postovi: (44)16
Spol: 
|
|
| [Vrh] |
|
spik2nick
Forumaš(ica)

Pridružen/a: 28. 09. 2011. (12:41:01)
Postovi: (D)16
|
|
| [Vrh] |
|
Optimum
Forumaš(ica)

Pridružen/a: 07. 09. 2011. (09:16:23)
Postovi: (41)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
PermutiranoPrase
Forumaš(ica)


Pridružen/a: 10. 09. 2011. (16:08:19)
Postovi: (F4)16
Spol: 
|
 Postano: 16:40 sri, 12. 10. 2011 Naslov: Postano: 16:40 sri, 12. 10. 2011 Naslov: |
    |
|
|
I ja imam jedno bedasto pitanje. Ok, par. Ili malo više nego par. I nisu vezana isključivo uz zadaće.
[b]1.zadatak glasi:[/b]
[latex]|x^2 - x| - |x| < 1[/latex]
Ja to sredih ovako:
[latex]|x||x-1|- |x| - 1 < 0[/latex]
[latex]x_1 = 0[/latex]
[latex]x_2 = 1[/latex]
1. slučaj: x<0
Raspišem, dobijem interval.
Uvrštavala sam u ovo:
[latex]|x||x-1|- |x| - 1 < 0[/latex]
Hoće li zagrada cijela imati predznak minus:[latex]-(x-1)[/latex]
ili ću pisati[latex] (-x - 1)?[/latex]
Drugi slučaj: 0<x<1
Treći slučaj: x>1
Dobijem tri intervala kao rješenja pojedinih slučajeva.
Konačno rješenje je unija ta tri rješenja? Ili njihov presjek? Ili nema konačnog rješenja nego samo rješenje po intervalima?
Davno sam radila module, malo zaboravih neke stvari. :oops:
[b]2. Kako dokazati:[/b]
[latex] \dfrac{|a+b| + |a-b|}{2ab} = \dfrac{sgn(ab)}{min(|a|,|b|)}[/latex]
Počela sam nešto raspisivati, pa shvatih da je tu nešto čudno. :)
[b]3. Ako želim provjeriti injektivnost funkcije[/b], postupam ovako:
Pretpostavim da je [latex]f(x_1) = f(x2) => x_1 = x_2[/latex], pa umjesto [latex]f(x_1), f(x_2) [/latex] pišem izraze, sredim ih, pa na kraju kad se sve i svašta pokrati, poništi, oduzme i sl. dobijem [latex]5x_1 = 5x_2 [/latex], tj. [latex]x_1 = x_2 [/latex].
[b]4. A kako provjeravam surjekciju?[/b] (Nije u domaćem kog sam rješavala ali je donekle vezano.)
[b]5.[/b] [b]Ako mi zadatak glasi odredi sliku tog intervala (ili cijele funkcije) ili prasliku nekog drugog intervala[/b], kao rješenje će mi se priznati samo račun, a crtanje (graf) ne? Ako sve riješim preko grafa, to je 0 bodova u kolokviju?
Je li ovo dovoljno za napisati:
[latex]f(x) = \sqrt{3-2x}[/latex]
Domena:
[latex]3-2x \geq 0[/latex]
[latex]x \leq \frac{3}{2}[/latex]
[latex]D_f = <-\infty, \frac{3}{2}]}[/latex]
Slika:
[latex]R_f = {f(x) : x \in D_f} = { \sqrt{3-2x} : x \in <-\infty, \frac{3}{2}]} = [1, + \infty>[/latex]
Ili treba još detaljnije? Rekli su da pišemo u kolokvijima sve moguće detalje, kao da objašnjavamo djeci u vrtiću, pa sad....
I ja imam jedno bedasto pitanje. Ok, par. Ili malo više nego par. I nisu vezana isključivo uz zadaće.
1.zadatak glasi:

Ja to sredih ovako:

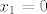
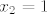
1. slučaj: x<0
Raspišem, dobijem interval.
Uvrštavala sam u ovo:

Hoće li zagrada cijela imati predznak minus: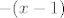
ili ću pisati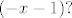
Drugi slučaj: 0<x<1
Treći slučaj: x>1
Dobijem tri intervala kao rješenja pojedinih slučajeva.
Konačno rješenje je unija ta tri rješenja? Ili njihov presjek? Ili nema konačnog rješenja nego samo rješenje po intervalima?
Davno sam radila module, malo zaboravih neke stvari. 
2. Kako dokazati:
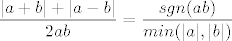
Počela sam nešto raspisivati, pa shvatih da je tu nešto čudno. 
3. Ako želim provjeriti injektivnost funkcije, postupam ovako:
Pretpostavim da je 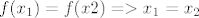 , pa umjesto , pa umjesto 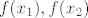 pišem izraze, sredim ih, pa na kraju kad se sve i svašta pokrati, poništi, oduzme i sl. dobijem pišem izraze, sredim ih, pa na kraju kad se sve i svašta pokrati, poništi, oduzme i sl. dobijem 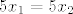 , tj. , tj. 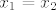 . .
4. A kako provjeravam surjekciju? (Nije u domaćem kog sam rješavala ali je donekle vezano.)
5. Ako mi zadatak glasi odredi sliku tog intervala (ili cijele funkcije) ili prasliku nekog drugog intervala, kao rješenje će mi se priznati samo račun, a crtanje (graf) ne? Ako sve riješim preko grafa, to je 0 bodova u kolokviju?
Je li ovo dovoljno za napisati:
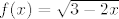
Domena:
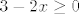
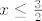
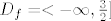
Slika:
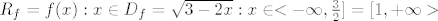
Ili treba još detaljnije? Rekli su da pišemo u kolokvijima sve moguće detalje, kao da objašnjavamo djeci u vrtiću, pa sad....
|
|
| [Vrh] |
|
Vishykc
Forumaš(ica)


Pridružen/a: 23. 10. 2010. (14:38:08)
Postovi: (6A)16
Spol: 
Lokacija: Zagreb
|
 Postano: 17:31 sri, 12. 10. 2011 Naslov: Postano: 17:31 sri, 12. 10. 2011 Naslov: |
    |
|
|
[quote="PermutiranoPrase"]I ja imam jedno bedasto pitanje. Ok, par. Ili malo više nego par. :D
[b]1.zadatak glasi:[/b]
[latex]|x^2 - x| - |x| < 1[/latex]
Ja to sredih ovako:
[latex]|x||x-1|- |x| - 1 < 0[/latex]
[latex]x_1 = 0[/latex]
[latex]x_2 = 1[/latex]
1. slučaj: x<0
Raspišem, dobijem interval.
Uvrštavala sam u ovo:
[latex]|x||x-1|- |x| - 1 < 0[/latex]. Očito za svaki y iz kodomene postoji jedinstveni x t.d f(x)=y.
Hoće li zagrada |x-1| cijela imati predznak minus:
[latex]-(x-1)[/latex]
ili ću pisati[latex] (-x - 1)?[/latex]
Drugi slučaj: 0<x<1
Treći slučaj: x>1
Dobijem tri intervala kao rješenja pojedinih slučajeva.
Konačno rješenje je unija ta tri rješenja? Ili njihov presjek? Ili nema konačnog rješenja nego samo rješenje po intervalima?
Davno sam radila module, malo zaboravih neke stvari. :oops:
[b]2. Kako dokazati:[/b]
[latex] \dfrac{|a+b| + |a-b|}{2ab} = \dfrac{sgn(ab)}{min(|a|,|b|)}[/latex]
Počela sam nešto raspisivati, pa shvatih da je tu nešto čudno. :)
[b]3. Ako želim provjeriti injektivnost funkcije[/b], postupam ovako:
Pretpostavim da je [latex]f(x_1) = f(x2) => x_1 = x_2[/latex], pa umjesto [latex]f(x_1), f(x_2) [/latex] pišem izraze, sredim ih, pa na kraju kad se sve i svašta pokrati, poništi, oduzme i sl. dobijem [latex]5x_1 = 5x_2 [/latex], tj. [latex]x_1 = x_2 [/latex].
[b]4. A kako provjeravam surjekciju?[/b] (Nije u domaćem kog sam rješavala ali je donekle vezano.)
[b]5.[/b] [b]Ako mi zadatak glasi odredi sliku tog intervala ili prasliku nekog drugog intervala[/b], kao rješenje će mi se priznati samo račun, a crtanje (graf) ne? Ako sve riješim preko grafa, to je 0 bodova u kolokviju?[/quote]
Da, samo trebaš kod raspisa na manjim intervalima "prešamarati" po cijelom [latex]\mathbb{R}[/latex]. Znači, drugi slučaj [latex]0\le x<1[/latex], a 3. [latex]x\ge 1[/latex]. Gledaš za x-eve jel manje od nule [b]ili[/b] u nekom od intervala pa je konačno rješenje unija sva tri slučaja . (Ali rješenje svakog slučaja je dani uvjet presječen s intervalom koji dobiješ rješivši nejednanžbu jer je to zadovoljeno za x-eve za koje vrijedi uvjet [b]i[/b] interval koji dobiješ) Za injekciju je dobro provjerit tak kak si napisala. Za surjekciju treba provjerit da za [b]svaki[/b] y iz kodomene postoji barem jedan x iz domene t.d je f(x)=y. Npr. za lin. funkciju f(x)=2x+3 rješavaš jednadžbu 2x+3=y po nepoznanici x. Slijedi da je [latex]x=\frac {y-3} {2}[/latex] :wink:
| PermutiranoPrase (napisa): | I ja imam jedno bedasto pitanje. Ok, par. Ili malo više nego par. 
1.zadatak glasi:

Ja to sredih ovako:

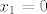
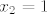
1. slučaj: x<0
Raspišem, dobijem interval.
Uvrštavala sam u ovo:
 . Očito za svaki y iz kodomene postoji jedinstveni x t.d f(x)=y. . Očito za svaki y iz kodomene postoji jedinstveni x t.d f(x)=y.
Hoće li zagrada |x-1| cijela imati predznak minus:
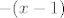
ili ću pisati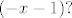
Drugi slučaj: 0<x<1
Treći slučaj: x>1
Dobijem tri intervala kao rješenja pojedinih slučajeva.
Konačno rješenje je unija ta tri rješenja? Ili njihov presjek? Ili nema konačnog rješenja nego samo rješenje po intervalima?
Davno sam radila module, malo zaboravih neke stvari. 
2. Kako dokazati:
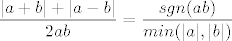
Počela sam nešto raspisivati, pa shvatih da je tu nešto čudno. 
3. Ako želim provjeriti injektivnost funkcije, postupam ovako:
Pretpostavim da je 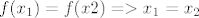 , pa umjesto , pa umjesto 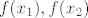 pišem izraze, sredim ih, pa na kraju kad se sve i svašta pokrati, poništi, oduzme i sl. dobijem pišem izraze, sredim ih, pa na kraju kad se sve i svašta pokrati, poništi, oduzme i sl. dobijem 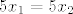 , tj. , tj. 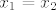 . .
4. A kako provjeravam surjekciju? (Nije u domaćem kog sam rješavala ali je donekle vezano.)
5. Ako mi zadatak glasi odredi sliku tog intervala ili prasliku nekog drugog intervala, kao rješenje će mi se priznati samo račun, a crtanje (graf) ne? Ako sve riješim preko grafa, to je 0 bodova u kolokviju? |
Da, samo trebaš kod raspisa na manjim intervalima "prešamarati" po cijelom  . Znači, drugi slučaj . Znači, drugi slučaj 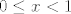 , a 3. , a 3. 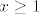 . Gledaš za x-eve jel manje od nule ili u nekom od intervala pa je konačno rješenje unija sva tri slučaja . (Ali rješenje svakog slučaja je dani uvjet presječen s intervalom koji dobiješ rješivši nejednanžbu jer je to zadovoljeno za x-eve za koje vrijedi uvjet i interval koji dobiješ) Za injekciju je dobro provjerit tak kak si napisala. Za surjekciju treba provjerit da za svaki y iz kodomene postoji barem jedan x iz domene t.d je f(x)=y. Npr. za lin. funkciju f(x)=2x+3 rješavaš jednadžbu 2x+3=y po nepoznanici x. Slijedi da je . Gledaš za x-eve jel manje od nule ili u nekom od intervala pa je konačno rješenje unija sva tri slučaja . (Ali rješenje svakog slučaja je dani uvjet presječen s intervalom koji dobiješ rješivši nejednanžbu jer je to zadovoljeno za x-eve za koje vrijedi uvjet i interval koji dobiješ) Za injekciju je dobro provjerit tak kak si napisala. Za surjekciju treba provjerit da za svaki y iz kodomene postoji barem jedan x iz domene t.d je f(x)=y. Npr. za lin. funkciju f(x)=2x+3 rješavaš jednadžbu 2x+3=y po nepoznanici x. Slijedi da je 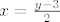 
_________________
U matematici se sve smije, osim pogriješiti!
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 17:45 sri, 12. 10. 2011 Naslov: Postano: 17:45 sri, 12. 10. 2011 Naslov: |
    |
|
|
[quote="PermutiranoPrase"]Hoće li zagrada |x-1| cijela imati predznak minus:[/quote]
Ako je x<0, onda je očito i x-1<0. Stavi a=x-1. Jer je a<0, onda je -a>0 pa je |x-1|=|a|=-a=-(x-1).
[quote]
Drugi slučaj: 0<x<1
Treći slučaj: x>1[/quote]
Uzmi u obzir da tvoja tri slučaja ništa ne govore o x=0 ili x=1.
[quote]Konačno rješenje je unija ta tri rješenja? Ili njihov presjek?[/quote]
Ako je [tex]I_1[/tex] rješenje slučaja x<0, [tex]I_2[/tex] rješenje slučaja [tex]0\leq x<1[/tex], a [tex]I_3[/tex] rješenje slučaja [tex]x\geq 1[/tex], onda ti je konačno rješenje
[tex](I_1 \cap \left\langle -\infty,0\right\rangle)\cup (I_2 \cap \left[0,1\right\rangle)\cup(I_3\cap\left[1,+\infty\right\rangle).[/tex]
U zagradama su presjeci jer, npr. u slučaju x<0, nejednadžba je zadovoljena za x<0 [b]i[/b] za x iz [tex]I_1[/tex]. Između zagrada je unija jer ili je [tex]x<0[/tex] i x iz [tex]I_1[/tex] ili je [tex]0\leq x <1[/tex] i x iz [tex]I_2[/tex] ili je [tex]x\geq 1[/tex] i x iz [tex]I_3 [/tex]
Vodi se za tim da [tex]a\cup b[/tex] znači a ili b, a [tex]a\cap b[/tex] znači a i b.
[quote]
[b]2. Kako dokazati:[/b]
[latex] \dfrac{|a+b| + |a-b|}{2ab} = \dfrac{sgn(ab)}{min(|a|,|b|)}[/latex]
Počela sam nešto raspisivati, pa shvatih da je tu nešto čudno. :)[/quote]
Imaš dva slučaja: a<b i a=b. Slučaj a>b je isto što i a<b, radi se samo o zamijeni simbola. Pretpostavi da je a=b. Onda je |a|=|b| pa je min{|a|,|b|}=min{|a|,|a|}=|a|. Još je |a-b|=0 i sgn(ab)=1 (jer su ili oba pozitivni ili oba negativni). Ako kreneš s lijeve strane, onda dobivaš
[tex]\frac{|a+a|+0}{2a^2}=\frac{|a|}{|a|^2}=\frac{1}{|a|}=\frac{sgn(ab)}{min(|a|,|b|)}.[/tex]
Slučaj a<b slično dokazuješ, samo moraš još promatrati slučajeve kada su a i b različitog i kada su istog predznaka.
[quote][b]3. Ako želim provjeriti injektivnost funkcije[/b], postupam ovako:
Pretpostavim da je [latex]f(x_1) = f(x2) => x_1 = x_2[/latex], pa umjesto [latex]f(x_1), f(x_2) [/latex] pišem izraze, sredim ih, pa na kraju kad se sve i svašta pokrati, poništi, oduzme i sl. dobijem [latex]5x_1 = 5x_2 [/latex], tj. [latex]x_1 = x_2 [/latex].[/quote]
Ne pretpostavljaš [latex]f(x_1) = f(x_2) \Rightarrow x_1 = x_2[/latex]. Pretpostavljaš [latex]f(x_1) = f(x_2)[/latex] i želiš dokazati da iz toga slijedi [latex]x_1=x_2[/latex].
[quote][b]4. A kako provjeravam surjekciju?[/b] (Nije u domaćem kog sam rješavala ali je donekle vezano.)[/quote]
Općenito nema šablone. Može se provjeriti po definiciji, tj. za svaki y iz kodomene eksplicitno nađeš x iz domene td. je f(x)=y, što zna biti i nešto teže kada su domena i kodomena beskonačne. Kada su i domena i kodomena konačne, onda se iskoristi jeftin trik da je funkcija surjekcija ako i samo ako je injekcija.
U posebnim slučajevima, kada se radi o "lijepim" funkcijama (neprekidnima, definiranima na kompaktnom skupu, derivabilnima itd.) možeš se poslužiti nekim od teorema koji govore koje sve vrijednosti funkcija može poprimiti, a koje ćeš uskoro naučiti. :)
[quote][b]5.[/b] [b]Ako mi zadatak glasi odredi sliku tog intervala ili prasliku nekog drugog intervala[/b], kao rješenje će mi se priznati samo račun, a crtanje (graf) ne? Ako sve riješim preko grafa, to je 0 bodova u kolokviju?[/quote]
Graf je samo skica koja tebi služi da si predočiš što bi rješenje moglo biti. Npr. ako zadatak glasi, odredi sliku intervala x>1 te i te funkcije, onda iz grafa ne možeš očitati da li se za npr. x=5 323 221 334 447 893 211 počne nešto čudno događati s funkcijom.
| PermutiranoPrase (napisa): | | Hoće li zagrada |x-1| cijela imati predznak minus: |
Ako je x<0, onda je očito i x-1<0. Stavi a=x-1. Jer je a<0, onda je -a>0 pa je |x-1|=|a|=-a=-(x-1).
| Citat: |
Drugi slučaj: 0<x<1
Treći slučaj: x>1 |
Uzmi u obzir da tvoja tri slučaja ništa ne govore o x=0 ili x=1.
| Citat: | | Konačno rješenje je unija ta tri rješenja? Ili njihov presjek? |
Ako je [tex]I_1[/tex] rješenje slučaja x<0, [tex]I_2[/tex] rješenje slučaja [tex]0\leq x<1[/tex], a [tex]I_3[/tex] rješenje slučaja [tex]x\geq 1[/tex], onda ti je konačno rješenje
[tex](I_1 \cap \left\langle -\infty,0\right\rangle)\cup (I_2 \cap \left[0,1\right\rangle)\cup(I_3\cap\left[1,+\infty\right\rangle).[/tex]
U zagradama su presjeci jer, npr. u slučaju x<0, nejednadžba je zadovoljena za x<0 i za x iz [tex]I_1[/tex]. Između zagrada je unija jer ili je [tex]x<0[/tex] i x iz [tex]I_1[/tex] ili je [tex]0\leq x <1[/tex] i x iz [tex]I_2[/tex] ili je [tex]x\geq 1[/tex] i x iz [tex]I_3 [/tex]
Vodi se za tim da [tex]a\cup b[/tex] znači a ili b, a [tex]a\cap b[/tex] znači a i b.
| Citat: |
2. Kako dokazati:
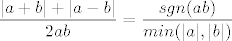
Počela sam nešto raspisivati, pa shvatih da je tu nešto čudno.  |
Imaš dva slučaja: a<b i a=b. Slučaj a>b je isto što i a<b, radi se samo o zamijeni simbola. Pretpostavi da je a=b. Onda je |a|=|b| pa je min{|a|,|b|}=min{|a|,|a|}=|a|. Još je |a-b|=0 i sgn(ab)=1 (jer su ili oba pozitivni ili oba negativni). Ako kreneš s lijeve strane, onda dobivaš
[tex]\frac{|a+a|+0}{2a^2}=\frac{|a|}{|a|^2}=\frac{1}{|a|}=\frac{sgn(ab)}{min(|a|,|b|)}.[/tex]
Slučaj a<b slično dokazuješ, samo moraš još promatrati slučajeve kada su a i b različitog i kada su istog predznaka.
| Citat: | 3. Ako želim provjeriti injektivnost funkcije, postupam ovako:
Pretpostavim da je 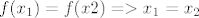 , pa umjesto , pa umjesto 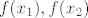 pišem izraze, sredim ih, pa na kraju kad se sve i svašta pokrati, poništi, oduzme i sl. dobijem pišem izraze, sredim ih, pa na kraju kad se sve i svašta pokrati, poništi, oduzme i sl. dobijem 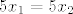 , tj. , tj. 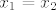 . . |
Ne pretpostavljaš 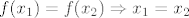 . Pretpostavljaš . Pretpostavljaš 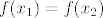 i želiš dokazati da iz toga slijedi i želiš dokazati da iz toga slijedi 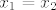 . .
| Citat: | | 4. A kako provjeravam surjekciju? (Nije u domaćem kog sam rješavala ali je donekle vezano.) |
Općenito nema šablone. Može se provjeriti po definiciji, tj. za svaki y iz kodomene eksplicitno nađeš x iz domene td. je f(x)=y, što zna biti i nešto teže kada su domena i kodomena beskonačne. Kada su i domena i kodomena konačne, onda se iskoristi jeftin trik da je funkcija surjekcija ako i samo ako je injekcija.
U posebnim slučajevima, kada se radi o "lijepim" funkcijama (neprekidnima, definiranima na kompaktnom skupu, derivabilnima itd.) možeš se poslužiti nekim od teorema koji govore koje sve vrijednosti funkcija može poprimiti, a koje ćeš uskoro naučiti. 
| Citat: | | 5. Ako mi zadatak glasi odredi sliku tog intervala ili prasliku nekog drugog intervala, kao rješenje će mi se priznati samo račun, a crtanje (graf) ne? Ako sve riješim preko grafa, to je 0 bodova u kolokviju? |
Graf je samo skica koja tebi služi da si predočiš što bi rješenje moglo biti. Npr. ako zadatak glasi, odredi sliku intervala x>1 te i te funkcije, onda iz grafa ne možeš očitati da li se za npr. x=5 323 221 334 447 893 211 počne nešto čudno događati s funkcijom.
_________________
The Dude Abides
Zadnja promjena: goranm; 18:51 sri, 12. 10. 2011; ukupno mijenjano 6 put/a.
|
|
| [Vrh] |
|
logikaus
Forumaš(ica)

Pridružen/a: 12. 10. 2011. (17:55:23)
Postovi: (45)16
|
|
| [Vrh] |
|
|












