| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
logikaus
Forumaš(ica)

Pridružen/a: 12. 10. 2011. (17:55:23)
Postovi: (45)16
|
 Postano: 14:58 sub, 15. 10. 2011 Naslov: domaće zadaće 1 i 2 - rješenja Postano: 14:58 sub, 15. 10. 2011 Naslov: domaće zadaće 1 i 2 - rješenja |
    |
|
|
idea je da svatko stavi rješenja onih zadataka koje je riješio tako da možemo usporediti dobivena rješenja i vidjeti gdje smo progriješili :D
ako ste za ^^
npr.
1. a) xe < -1/2, 1 >
b) xe < -bes,1>U<4,+besk>
7. λe <-1,3>
10. dokaže se za je korijen iz 2 irac. br. (to smo radili kod guljaša), analogno za korijen z 3 i onda je njihov zbroj iracionalan broj
idea je da svatko stavi rješenja onih zadataka koje je riješio tako da možemo usporediti dobivena rješenja i vidjeti gdje smo progriješili 
ako ste za ^^
npr.
1. a) xe < -1/2, 1 >
b) xe < -bes,1>U<4,+besk>
7. λe <-1,3>
10. dokaže se za je korijen iz 2 irac. br. (to smo radili kod guljaša), analogno za korijen z 3 i onda je njihov zbroj iracionalan broj
|
|
| [Vrh] |
|
wrathchild
Forumaš(ica)

Pridružen/a: 09. 07. 2010. (21:25:00)
Postovi: (31)16
|
|
| [Vrh] |
|
kikota
Forumaš(ica)

Pridružen/a: 25. 09. 2011. (17:09:30)
Postovi: (22)16
Spol: 
Lokacija: Dalmacijaa <3
|
|
| [Vrh] |
|
wrathchild
Forumaš(ica)


Pridružen/a: 09. 07. 2010. (21:25:00)
Postovi: (31)16
|
|
| [Vrh] |
|
logikaus
Forumaš(ica)

Pridružen/a: 12. 10. 2011. (17:55:23)
Postovi: (45)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
 Postano: 16:58 sub, 15. 10. 2011 Naslov: Postano: 16:58 sub, 15. 10. 2011 Naslov: |
    |
|
|
[quote="kikota"]... pa se nameće pitanje mora li zbroj dva racionalna broja biti racionalan?...[/quote]
Zbroj 2 racionalna je uvijek racionalan.
[quote="logikaus"]al ovo je zbroj dva pozitivna iracionalna broja, pa ako se to napomene, onda je ta tvrdnja tocna :D (valjda xD)[/quote]
To ne vrijedi, uzmi [latex]a=\sqrt{2} +1[/latex], [latex]b=5-\sqrt{2}[/latex].
Oba su broja iracionalna, a njihov zbroj je prirodan broj.
10. Dokazi da je [latex]\sqrt{2}+\sqrt{3}[/latex] iracionalan.
Pretpostavimo suprotno, da je racionalan. Sad je [latex]\sqrt{2}+\sqrt{3}=\frac{m}{n}[/latex] gdje su [latex]m,n[/latex] prirodni brojevi.
Kvadriram i sredjujem: [latex]\sqrt{6}=\frac{\frac{m^2}{n^2}-5}{2}[/latex]. Desna strana je racionalan broj, dok lijeva strana nije, kontradikcija.
| kikota (napisa): | | ... pa se nameće pitanje mora li zbroj dva racionalna broja biti racionalan?... |
Zbroj 2 racionalna je uvijek racionalan.
| logikaus (napisa): | al ovo je zbroj dva pozitivna iracionalna broja, pa ako se to napomene, onda je ta tvrdnja tocna  (valjda xD) (valjda xD) |
To ne vrijedi, uzmi 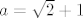 , , 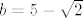 . .
Oba su broja iracionalna, a njihov zbroj je prirodan broj.
10. Dokazi da je  iracionalan. iracionalan.
Pretpostavimo suprotno, da je racionalan. Sad je 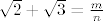 gdje su gdje su 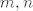 prirodni brojevi. prirodni brojevi.
Kvadriram i sredjujem: 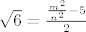 . Desna strana je racionalan broj, dok lijeva strana nije, kontradikcija. . Desna strana je racionalan broj, dok lijeva strana nije, kontradikcija.
|
|
| [Vrh] |
|
Silenoz
Forumaš(ica)


Pridružen/a: 15. 10. 2011. (18:45:11)
Postovi: (4F)16
Spol: 
|
 Postano: 19:02 sub, 15. 10. 2011 Naslov: Postano: 19:02 sub, 15. 10. 2011 Naslov: |
    |
|
|
Bok, može netko reći kako se 29. iz prve zadaće rješava?
Petljao sam nešto, pa išao preko geometrijskog niza, uglavnom poprilično sam pojednostavnio ali nemam ideju kako do kraja. Može pomoć?
I par pitanja, treba li po 5 velikih zadataka sa svim a),b),.. predati ili se ti mali broje?
I hoće li na ispitima biti dopuštene ikakve formule? Evo sad kad rješavam skužim koja mi formula treba ali znati je baš točno napamet već je problem.
Bok, može netko reći kako se 29. iz prve zadaće rješava?
Petljao sam nešto, pa išao preko geometrijskog niza, uglavnom poprilično sam pojednostavnio ali nemam ideju kako do kraja. Može pomoć?
I par pitanja, treba li po 5 velikih zadataka sa svim a),b),.. predati ili se ti mali broje?
I hoće li na ispitima biti dopuštene ikakve formule? Evo sad kad rješavam skužim koja mi formula treba ali znati je baš točno napamet već je problem.
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
Sino
Forumaš(ica)


Pridružen/a: 06. 10. 2011. (14:09:58)
Postovi: (14)16
Spol: 
|
|
| [Vrh] |
|
Silenoz
Forumaš(ica)


Pridružen/a: 15. 10. 2011. (18:45:11)
Postovi: (4F)16
Spol: 
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
 Postano: 20:39 sub, 15. 10. 2011 Naslov: Postano: 20:39 sub, 15. 10. 2011 Naslov: |
    |
|
|
[quote="kikota"]ali za dokaz pretpostavljamo suprotno, pa se nameće pitanje mora li zbroj dva racionalna broja biti racionalan?? po meni mora, al ja san glupa, pa moze li netko odg. jeli to točno??[/quote]
Dva racionalna broja mora biti racionalan broj. Npr, neka je [tex]p = \frac{a}{b}, q = \frac{c}{d}, a, c \in \mathbb{Z}, b, d \in \mathbb{N}[/tex], pa je i [tex]p, q \in \mathbb{Q}[/tex]. Pitanje je da li vrijedi [tex]p+q \in \mathbb{Q}[/tex]?
[tex]p + q = \frac{a}{b}+ \frac{c}{d} = \frac{ad+bc}{bc}[/tex]. Kako su [tex]a, c \in \mathbb{Z}, b, d \in \mathbb{N}[/tex], i kako je [tex]\mathbb{Z} [/tex] zatvoren za zbrajanje i množenje (što hoće reći da pri zbrajanju i množenju dobivamo rezultat koji je ponovno u tom skupu!), to vrijedi da je [tex]ad+bc \in \mathbb{Z}[/tex]. Slično, kako je [tex]\mathbb{N}[/tex] zatvoren za množenje, to će biti da je [tex]bd \in \mathbb{N}[/tex]. Te činjenici u konačnici dokazuju da je [tex]p+q \in \mathbb{Q}[/tex], odnosno da je suma dvaju racionalnih brojeva racionalan broj.
| kikota (napisa): | | ali za dokaz pretpostavljamo suprotno, pa se nameće pitanje mora li zbroj dva racionalna broja biti racionalan?? po meni mora, al ja san glupa, pa moze li netko odg. jeli to točno?? |
Dva racionalna broja mora biti racionalan broj. Npr, neka je [tex]p = \frac{a}{b}, q = \frac{c}{d}, a, c \in \mathbb{Z}, b, d \in \mathbb{N}[/tex], pa je i [tex]p, q \in \mathbb{Q}[/tex]. Pitanje je da li vrijedi [tex]p+q \in \mathbb{Q}[/tex]?
[tex]p + q = \frac{a}{b}+ \frac{c}{d} = \frac{ad+bc}{bc}[/tex]. Kako su [tex]a, c \in \mathbb{Z}, b, d \in \mathbb{N}[/tex], i kako je [tex]\mathbb{Z} [/tex] zatvoren za zbrajanje i množenje (što hoće reći da pri zbrajanju i množenju dobivamo rezultat koji je ponovno u tom skupu!), to vrijedi da je [tex]ad+bc \in \mathbb{Z}[/tex]. Slično, kako je [tex]\mathbb{N}[/tex] zatvoren za množenje, to će biti da je [tex]bd \in \mathbb{N}[/tex]. Te činjenici u konačnici dokazuju da je [tex]p+q \in \mathbb{Q}[/tex], odnosno da je suma dvaju racionalnih brojeva racionalan broj.
_________________
Dvije stvari su beskonacne: svemir i ljudska glupost. Za ono prvo nisam siguran.
by A.Einstein
Zadnja promjena: kenny; 0:38 ned, 16. 10. 2011; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
pantoni
Forumaš(ica)
Pridružen/a: 14. 09. 2011. (19:32:20)
Postovi: (8)16
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
|
| [Vrh] |
|
pantoni
Forumaš(ica)
Pridružen/a: 14. 09. 2011. (19:32:20)
Postovi: (8)16
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
 Postano: 18:59 ned, 16. 10. 2011 Naslov: Postano: 18:59 ned, 16. 10. 2011 Naslov: |
    |
|
|
[quote="pantoni"]moze li pomoc oko 7 zadatka iz prve zadace?[/quote]
Naprimjer ovako:
U ovom specijalnom slucaju lako je faktorizirati jednadzbu i vidjeti da su joj rjesenja [tex]\lambda-1[/tex], [tex]\lambda+1[/tex]. Dalje je sada lako.
[size=9][color=#999999]Added after 14 minutes:[/color][/size]
[quote="Silenoz"]Ja sam na ovaj nacin isao, krivo je, jel da?
Ako odmah iskoristim geometrijski niz dobijem (sry na nekorištenju latexa još nisam naučio...):
(x^n)(2n+1)<=(x^(2n)-1)/(x-1) i nije da vidim neki pametan izlaz.[/quote]
Kad se pozbroji suma geometrijskog reda, nesto je teze elementarno vidjeti da nejednakost vrijedi.
Najbolje je nakon treceg reda u vasoj biljeznici primijetiti da vrijedi [tex]x^k + \frac{1}{x^k} \geq 2[/tex] za k=1,2,...,n.
Naime, nakon mnozenja s nazivnikom dobijete [tex](x^k-1)^2\geq 0[/tex].
| pantoni (napisa): | | moze li pomoc oko 7 zadatka iz prve zadace? |
Naprimjer ovako:
U ovom specijalnom slucaju lako je faktorizirati jednadzbu i vidjeti da su joj rjesenja [tex]\lambda-1[/tex], [tex]\lambda+1[/tex]. Dalje je sada lako.
Added after 14 minutes:
| Silenoz (napisa): | Ja sam na ovaj nacin isao, krivo je, jel da?
Ako odmah iskoristim geometrijski niz dobijem (sry na nekorištenju latexa još nisam naučio...):
(x^n)(2n+1)⇐(x^(2n)-1)/(x-1) i nije da vidim neki pametan izlaz. |
Kad se pozbroji suma geometrijskog reda, nesto je teze elementarno vidjeti da nejednakost vrijedi.
Najbolje je nakon treceg reda u vasoj biljeznici primijetiti da vrijedi [tex]x^k + \frac{1}{x^k} \geq 2[/tex] za k=1,2,...,n.
Naime, nakon mnozenja s nazivnikom dobijete [tex](x^k-1)^2\geq 0[/tex].
|
|
| [Vrh] |
|
pantoni
Forumaš(ica)
Pridružen/a: 14. 09. 2011. (19:32:20)
Postovi: (8)16
|
|
| [Vrh] |
|
hstojanovic
Forumaš(ica)
Pridružen/a: 16. 10. 2010. (18:00:01)
Postovi: (30)16
Spol: 
|
|
| [Vrh] |
|
jema
Forumaš(ica)

Pridružen/a: 29. 09. 2011. (15:56:35)
Postovi: (52)16
|
|
| [Vrh] |
|
hstojanovic
Forumaš(ica)
Pridružen/a: 16. 10. 2010. (18:00:01)
Postovi: (30)16
Spol: 
|
|
| [Vrh] |
|
jema
Forumaš(ica)

Pridružen/a: 29. 09. 2011. (15:56:35)
Postovi: (52)16
|
|
| [Vrh] |
|
|















