| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
 Postano: 16:23 čet, 27. 10. 2011 Naslov: zadaće za vježbu Postano: 16:23 čet, 27. 10. 2011 Naslov: zadaće za vježbu |
    |
|
|
http://web.math.hr/nastava/difraf/dif/2006-07/zadaca2.pdf
zadaci: 7, 10, 11. malo mi štekaju ti dokazi.
http://web.math.hr/nastava/difraf/dif/2008-09/nepr.pdf
zadaci: 1. pod d), k)
pod d) sam dobila da se funkcija može proširiti u (0,0) al mi opet šteka dokaz. ako se kome da raspisat, bila bih zahvalna.
pod k) sam dobila da mi je limes funkcije 0 što je jednako f(0,0). jel se tu treba još nešto dokazat il je to to?
unaprijed hvala
http://web.math.hr/nastava/difraf/dif/2006-07/zadaca2.pdf
zadaci: 7, 10, 11. malo mi štekaju ti dokazi.
http://web.math.hr/nastava/difraf/dif/2008-09/nepr.pdf
zadaci: 1. pod d), k)
pod d) sam dobila da se funkcija može proširiti u (0,0) al mi opet šteka dokaz. ako se kome da raspisat, bila bih zahvalna.
pod k) sam dobila da mi je limes funkcije 0 što je jednako f(0,0). jel se tu treba još nešto dokazat il je to to?
unaprijed hvala
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
sz
Forumaš(ica)


Pridružen/a: 26. 01. 2011. (15:17:39)
Postovi: (35)16
|
 Postano: 17:27 čet, 27. 10. 2011 Naslov: Postano: 17:27 čet, 27. 10. 2011 Naslov: |
    |
|
|
Zadaća 2:
7. Lako je pokazati da je niz Cauchyjev:
za [latex]\quad k, l \geq k_0 \quad d(a_k,a_l) \leq \frac{1}{k}+\frac{1}{l} \leq \frac{2}{k_0} < \epsilon \quad [/latex] ako smo uzeli dovoljno veliki [latex]k_0[/latex]
pa je i konvergentan zbog potpunosti od [latex]\mathbb{R}^n[/latex].
10. Skup je omeđen jer je svaki konvergentan niz u [latex]\mathbb{R}^n[/latex] omeđen, a zatvoren jer sadrži sva svoja gomilišta:
ako je neki [latex]x \in \mathbb{R}^n[/latex] njegovo gomilište, onda se u svakoj otvorenoj kugli sa središtem u njemu nalazi beskonačno mnogo elemenata skupa (zovimo ga) A pa je lako konstruirati konvergentan podniz početnog niza koji teži u x. Ali svaki podniz konvergentnog niza konvergira prema njegovu limesu, u našem slučaju a, pa bi nužno bilo x=a, ali onda je [latex]x \in A[/latex], što smo i htjeli pokazati.
Da, stvarno, 10. se može ljepše riješiti na cepsov način. Što mogu, zakržljah... :oops:
11. Pa, očito je niz [latex](a_k)[/latex] ograničen (slika mu je sadržana u [latex]K((0, 0), 2)[/latex]) pa ima konvergentan podniz (B-W).
1.d) U točkama prirodne domene (sve osim koordinatnih osi) očito je neprekidna jer bla bla...
Za točke [latex](x_0, 0)[/latex] gdje je [latex]x_0 \neq 0[/latex] npr. nizovi
[latex](x_0, \frac{1}{(2k+\frac{1}{2})\frac{\pi}{2}}) \to (x_0, 0)\quad[/latex] i [latex]\quad (x_0, \frac{1}{(2k+\frac{3}{2})\frac{\pi}{2}}) \to (x_0, 0)[/latex],
a njihove funkcijske vrijednosti idu u [latex] x_0 \sin \frac{1}{x_0}[/latex], odnosno [latex]-x_0 \sin \frac{1}{x_0}[/latex] pa fju ne možemo dodefinirati u tim točkama.
Analogno ako x i y zamijene uloge.
Ostaje (0, 0):
[latex]|(x+y)\sin\frac{1}{x}\sin\frac{1}{y}| \leq |x + y| \leq |x| + |y| \leq 2\sqrt{x^2+y^2} < \epsilon[/latex]
za [latex]d((x, y), (0, 0)) < \frac{\epsilon}{2}[/latex]
pa fju u (0, 0) možemo dodefinirati sa 0.
k) Jedina točka u kojoj fja nije definirana je (0, 0), pa, ako si pokazala da je limes fje u (0, 0) jednak 0, to znači da fju možeš dodefinirati u (0, 0) sa 0, i zadatak gotov. :)
Zadaća 2:
7. Lako je pokazati da je niz Cauchyjev:
za 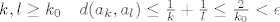 ako smo uzeli dovoljno veliki ako smo uzeli dovoljno veliki 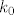
pa je i konvergentan zbog potpunosti od  . .
10. Skup je omeđen jer je svaki konvergentan niz u  omeđen, a zatvoren jer sadrži sva svoja gomilišta: omeđen, a zatvoren jer sadrži sva svoja gomilišta:
ako je neki  njegovo gomilište, onda se u svakoj otvorenoj kugli sa središtem u njemu nalazi beskonačno mnogo elemenata skupa (zovimo ga) A pa je lako konstruirati konvergentan podniz početnog niza koji teži u x. Ali svaki podniz konvergentnog niza konvergira prema njegovu limesu, u našem slučaju a, pa bi nužno bilo x=a, ali onda je njegovo gomilište, onda se u svakoj otvorenoj kugli sa središtem u njemu nalazi beskonačno mnogo elemenata skupa (zovimo ga) A pa je lako konstruirati konvergentan podniz početnog niza koji teži u x. Ali svaki podniz konvergentnog niza konvergira prema njegovu limesu, u našem slučaju a, pa bi nužno bilo x=a, ali onda je 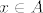 , što smo i htjeli pokazati. , što smo i htjeli pokazati.
Da, stvarno, 10. se može ljepše riješiti na cepsov način. Što mogu, zakržljah... 
11. Pa, očito je niz 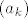 ograničen (slika mu je sadržana u ograničen (slika mu je sadržana u 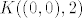 ) pa ima konvergentan podniz (B-W). ) pa ima konvergentan podniz (B-W).
1.d) U točkama prirodne domene (sve osim koordinatnih osi) očito je neprekidna jer bla bla...
Za točke 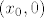 gdje je gdje je 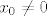 npr. nizovi npr. nizovi
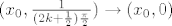 i i 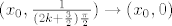 , ,
a njihove funkcijske vrijednosti idu u 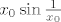 , odnosno , odnosno 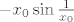 pa fju ne možemo dodefinirati u tim točkama. pa fju ne možemo dodefinirati u tim točkama.
Analogno ako x i y zamijene uloge.
Ostaje (0, 0):
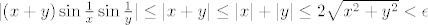
za 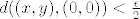
pa fju u (0, 0) možemo dodefinirati sa 0.
k) Jedina točka u kojoj fja nije definirana je (0, 0), pa, ako si pokazala da je limes fje u (0, 0) jednak 0, to znači da fju možeš dodefinirati u (0, 0) sa 0, i zadatak gotov. 
|
|
| [Vrh] |
|
sz
Forumaš(ica)


Pridružen/a: 26. 01. 2011. (15:17:39)
Postovi: (35)16
|
|
| [Vrh] |
|
888
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (18:26:14)
Postovi: (29)16
|
|
| [Vrh] |
|
sz
Forumaš(ica)


Pridružen/a: 26. 01. 2011. (15:17:39)
Postovi: (35)16
|
|
| [Vrh] |
|
888
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (18:26:14)
Postovi: (29)16
|
|
| [Vrh] |
|
rain
Forumaš(ica)

Pridružen/a: 02. 04. 2011. (13:58:42)
Postovi: (13)16
|
|
| [Vrh] |
|
sz
Forumaš(ica)


Pridružen/a: 26. 01. 2011. (15:17:39)
Postovi: (35)16
|
 Postano: 14:06 pon, 31. 10. 2011 Naslov: Postano: 14:06 pon, 31. 10. 2011 Naslov: |
    |
|
|
2. c) Budući da su [latex]\mathbb{Q}[/latex] i [latex]\mathbb{R} \backslash \mathbb{Q}[/latex] gusti u [latex]\mathbb{R}[/latex], lako je vidjeti da su i [latex]\mathbb{Q}^3[/latex] i [latex]\mathbb{R}^3 \backslash \mathbb{Q}^3 [/latex] gusti u [latex]\mathbb{R}^3[/latex], tj. u proizvoljnoj blizini neke točke iz [latex]\mathbb{R}^3[/latex] možemo naći i točku iz [latex]\mathbb{Q}^3[/latex] i točku iz [latex]\mathbb{R}^3 \backslash \mathbb{Q}^3[/latex], a to znači da u proizvoljnoj blizini točke [latex](x, y, z) \in \mathbb{R}^3[/latex] možemo naći i točke čija je funkcijska vrijednost proizvoljno blizu [latex]|x + y|[/latex] i točke čija je funkcijska vrijednost proizvoljno blizu [latex]-|y + z|[/latex], tj., ako hoćemo baš 100% precizno, možemo konstruirati niz točaka iz [latex]\mathbb{Q}^3[/latex] koji konvergira u [latex](x, y, z)[/latex] (a onda funkcijske vrijednosti tog niza teže u [latex]|x + y|[/latex]) i niz točaka iz [latex]\mathbb{R}^3 \backslash \mathbb{Q}^3[/latex] koji konvergira u [latex](x, y, z)[/latex] (a njegove funkcijske vrijednosti onda teže u [latex]-|y + z|[/latex]).
Da bi bila zadovoljena Heineova karakterizacija neprekidnosti, onda je za neprekidnost fje f u [latex](x, y, z)[/latex] nužno da bude [latex]|x + y| = -|y + z|[/latex], što je (zbog nenegativnosti apsolutne vrijednosti) moguće samo ako je [latex]|x + y| = |y + z| = 0[/latex], tj. za točke oblika [latex](x, -x, -x)[/latex], gdje je [latex]x \in \mathbb{R}[/latex].
To je i dovoljan uvjet (zašto?) pa je to to.
1. g) [latex]|\frac{x_1 \sin{x_1} + ... + x_n \sin{x_n}}{x_1^2 + ... + x_n^2} - 1| \leq[/latex]
[latex]\leq |\frac{x_1 \sin{x_1} - x_1^2}{x_1^2 + ... + x_n^2}| + ... + |\frac{x_n \sin{x_n} - x_n^2}{x_1^2 + ... + x_n^2}| \leq[/latex]
(ovdje ipak treba primijetiti da sljedeća ocjena nije OK ako je neki od [latex]x_i[/latex]-eva 0, ali u tom slučaju njegov član prije samog ocjenjivanja možemo i zaboraviti (ionako je 0))
[latex]\leq |\frac{x_1 \sin{x_1} - x_1^2}{x_1^2}| + ... + |\frac{x_n \sin{x_n} - x_n^2}{x_n^2}| = [/latex]
[latex]= |\frac{\sin{x_1}}{x_1} - 1| + ... + |\frac{\sin{x_n}}{x_n} - 1|[/latex]
To bi trebalo pomoći...
2. c) Budući da su 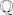 i i 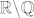 gusti u gusti u  , lako je vidjeti da su i , lako je vidjeti da su i 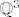 i i 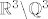 gusti u gusti u 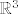 , tj. u proizvoljnoj blizini neke točke iz , tj. u proizvoljnoj blizini neke točke iz 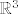 možemo naći i točku iz možemo naći i točku iz 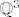 i točku iz i točku iz 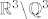 , a to znači da u proizvoljnoj blizini točke , a to znači da u proizvoljnoj blizini točke 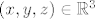 možemo naći i točke čija je funkcijska vrijednost proizvoljno blizu možemo naći i točke čija je funkcijska vrijednost proizvoljno blizu  i točke čija je funkcijska vrijednost proizvoljno blizu i točke čija je funkcijska vrijednost proizvoljno blizu 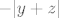 , tj., ako hoćemo baš 100% precizno, možemo konstruirati niz točaka iz , tj., ako hoćemo baš 100% precizno, možemo konstruirati niz točaka iz 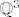 koji konvergira u koji konvergira u 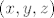 (a onda funkcijske vrijednosti tog niza teže u (a onda funkcijske vrijednosti tog niza teže u  ) i niz točaka iz ) i niz točaka iz 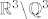 koji konvergira u koji konvergira u 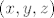 (a njegove funkcijske vrijednosti onda teže u (a njegove funkcijske vrijednosti onda teže u 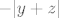 ). ).
Da bi bila zadovoljena Heineova karakterizacija neprekidnosti, onda je za neprekidnost fje f u 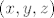 nužno da bude nužno da bude 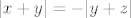 , što je (zbog nenegativnosti apsolutne vrijednosti) moguće samo ako je , što je (zbog nenegativnosti apsolutne vrijednosti) moguće samo ako je 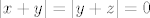 , tj. za točke oblika , tj. za točke oblika 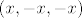 , gdje je , gdje je 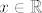 . .
To je i dovoljan uvjet (zašto?) pa je to to.
1. g) 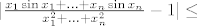
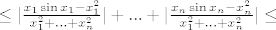
(ovdje ipak treba primijetiti da sljedeća ocjena nije OK ako je neki od 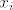 -eva 0, ali u tom slučaju njegov član prije samog ocjenjivanja možemo i zaboraviti (ionako je 0)) -eva 0, ali u tom slučaju njegov član prije samog ocjenjivanja možemo i zaboraviti (ionako je 0))
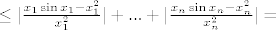
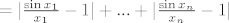
To bi trebalo pomoći...
|
|
| [Vrh] |
|
rain
Forumaš(ica)

Pridružen/a: 02. 04. 2011. (13:58:42)
Postovi: (13)16
|
|
| [Vrh] |
|
|




