| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
malalodacha
Forumaš(ica)

Pridružen/a: 11. 10. 2011. (17:06:13)
Postovi: (79)16
|
|
| [Vrh] |
|
Shaman
Forumaš(ica)


Pridružen/a: 24. 09. 2011. (22:21:43)
Postovi: (76)16
Spol: 
|
|
| [Vrh] |
|
malalodacha
Forumaš(ica)

Pridružen/a: 11. 10. 2011. (17:06:13)
Postovi: (79)16
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
|
| [Vrh] |
|
dodoria
Forumaš(ica)

Pridružen/a: 04. 10. 2011. (13:31:15)
Postovi: (E)16
|
 Postano: 20:27 uto, 1. 11. 2011 Naslov: Postano: 20:27 uto, 1. 11. 2011 Naslov: |
    |
|
|
Zadatak je s popravnog kolokvija, god. 2009./2010., 2., a ide ovako:
f(x)= ln(x/2) * ln(x/3).
Trazi se slika intervala [2,6] i praslika od [-1,0> .
Mislim da je očito da se ova gornja fja. treba prikazati kao kompozicija, odatle je zadatak relativno lagan, ali imam problema upravo s tim. Trebaju mi samo kompozicije, dakle, sami početak, pa ako je netko voljan raspisati taj dio. :?
P.S. Nisam još uhvatio korak s korištenjem ovog (La)Tex-a pa sam morao ovako pisati.
Zadatak je s popravnog kolokvija, god. 2009./2010., 2., a ide ovako:
f(x)= ln(x/2) * ln(x/3).
Trazi se slika intervala [2,6] i praslika od [-1,0> .
Mislim da je očito da se ova gornja fja. treba prikazati kao kompozicija, odatle je zadatak relativno lagan, ali imam problema upravo s tim. Trebaju mi samo kompozicije, dakle, sami početak, pa ako je netko voljan raspisati taj dio. 
P.S. Nisam još uhvatio korak s korištenjem ovog (La)Tex-a pa sam morao ovako pisati.
_________________
Dokaži.
|
|
| [Vrh] |
|
Shaman
Forumaš(ica)


Pridružen/a: 24. 09. 2011. (22:21:43)
Postovi: (76)16
Spol: 
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 11:08 sri, 2. 11. 2011 Naslov: Postano: 11:08 sri, 2. 11. 2011 Naslov: |
    |
|
|
Pretpostavimo da f nije injekcija.
Tada postoje x,y t.d. f(x)=f(y).
Ali onda uzmemo A={x,y}, B={y} pa je A\B={x}.
Sad imamo f(A\B)=f({x})=f(x) (neprazan skup)
s druge strane, f(A)=f(B) (jer f(x)=f(y)) pa je f(A)\f(B)=prazan skup
Iz gornja dva retka vidimo da je f(A\B) razlicito od f(A)\f(B), tj. dosli smo do kontradikcije => funkcija mora biti injektivna
Pretpostavimo da f nije injekcija.
Tada postoje x,y t.d. f(x)=f(y).
Ali onda uzmemo A={x,y}, B={y} pa je A\B={x}.
Sad imamo f(A\B)=f({x})=f(x) (neprazan skup)
s druge strane, f(A)=f(B) (jer f(x)=f(y)) pa je f(A)\f(B)=prazan skup
Iz gornja dva retka vidimo da je f(A\B) razlicito od f(A)\f(B), tj. dosli smo do kontradikcije => funkcija mora biti injektivna
|
|
| [Vrh] |
|
Shaman
Forumaš(ica)


Pridružen/a: 24. 09. 2011. (22:21:43)
Postovi: (76)16
Spol: 
|
|
| [Vrh] |
|
gamin
Forumaš(ica)

Pridružen/a: 19. 10. 2011. (19:02:37)
Postovi: (11)16
|
 Postano: 13:33 sri, 2. 11. 2011 Naslov: Postano: 13:33 sri, 2. 11. 2011 Naslov: |
    |
|
|
[quote="dodoria"]Zadatak je s popravnog kolokvija, god. 2009./2010., 2., a ide ovako:
f(x)= ln(x/2) * ln(x/3).
Trazi se slika intervala [2,6] i praslika od [-1,0> .
Mislim da je očito da se ova gornja fja. treba prikazati kao kompozicija, odatle je zadatak relativno lagan, ali imam problema upravo s tim. Trebaju mi samo kompozicije, dakle, sami početak, pa ako je netko voljan raspisati taj dio. :?
P.S. Nisam još uhvatio korak s korištenjem ovog (La)Tex-a pa sam morao ovako pisati.[/quote]
Mozda ovako:[latex]f(x)=(\ln x - \ln 2)(\ln x - \ln 3)[/latex].
Mnozenjem dobivamo [latex]f(x)=(\ln x)^2 - \ln x(\ln 2+\ln 3)+\ln 2\ln 3[/latex].
Sada rastavimo na kompoziciju [latex]f=f_2\circ f_1[/latex] gdje je [latex]f_1(x)=\ln x[/latex], a [latex]f_2(x)= x^2 - x(\ln 2+\ln 3))+\ln 2\ln 3[/latex].
Zatim odredimo [latex]f_1(\[2,6\])=\[\ln 2,\ln 6\]=\[\ln 2,\ln2+\ln 3\][/latex].
Onda nacrtamo graf za [latex]f_2[/latex], i dobijemo otprilike [b][url=http://www.wolframalpha.com/input/?i=plot+f%28x%29%3Dx%5E2+-+x%28log%282%29+%2B+log%283%29%29+%2Blog%282%29log%283%29]ovo[/url][/b](mislim da su nultocke [latex]x_1=\ln 2[/latex], [latex]x_2=\ln 3[/latex]).
I na kraju bi tebalo ispasti da je [latex]f_2(\[\ln 2,\ln 6\])=\[\displaystyle\frac{-(\ln 2 - \ln 3)^2}{4},\ln 2\ln 3\][/latex].Evo tako nekako otprilike. (nadam se da je tocno :))
A prasliku odredis racunski,tj gledas [latex]-1\leq\ln \displaystyle\frac{x}{2}\ln \displaystyle\frac{x}{3}<0[/latex].
| dodoria (napisa): | Zadatak je s popravnog kolokvija, god. 2009./2010., 2., a ide ovako:
f(x)= ln(x/2) * ln(x/3).
Trazi se slika intervala [2,6] i praslika od [-1,0> .
Mislim da je očito da se ova gornja fja. treba prikazati kao kompozicija, odatle je zadatak relativno lagan, ali imam problema upravo s tim. Trebaju mi samo kompozicije, dakle, sami početak, pa ako je netko voljan raspisati taj dio. 
P.S. Nisam još uhvatio korak s korištenjem ovog (La)Tex-a pa sam morao ovako pisati. |
Mozda ovako: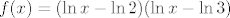 . .
Mnozenjem dobivamo 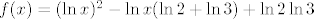 . .
Sada rastavimo na kompoziciju 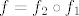 gdje je gdje je 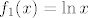 , a , a 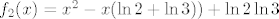 . .
Zatim odredimo 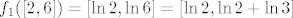 . .
Onda nacrtamo graf za 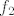 , i dobijemo otprilike ovo(mislim da su nultocke , i dobijemo otprilike ovo(mislim da su nultocke 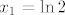 , , 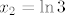 ). ).
I na kraju bi tebalo ispasti da je 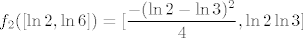 .Evo tako nekako otprilike. (nadam se da je tocno .Evo tako nekako otprilike. (nadam se da je tocno  ) )
A prasliku odredis racunski,tj gledas 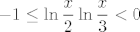 . .
Zadnja promjena: gamin; 13:51 sri, 2. 11. 2011; ukupno mijenjano 3 put/a.
|
|
| [Vrh] |
|
sailor m
Forumaš(ica)
Pridružen/a: 23. 10. 2010. (10:46:13)
Postovi: (4E)16
|
 Postano: 13:43 sri, 2. 11. 2011 Naslov: Postano: 13:43 sri, 2. 11. 2011 Naslov: |
    |
|
|
[quote="dodoria"]Zadatak je s popravnog kolokvija, god. 2009./2010., 2., a ide ovako:
f(x)= ln(x/2) * ln(x/3).
Trazi se slika intervala [2,6] i praslika od [-1,0> .
Mislim da je očito da se ova gornja fja. treba prikazati kao kompozicija, odatle je zadatak relativno lagan, ali imam problema upravo s tim. Trebaju mi samo kompozicije, dakle, sami početak, pa ako je netko voljan raspisati taj dio. :?
P.S. Nisam još uhvatio korak s korištenjem ovog (La)Tex-a pa sam morao ovako pisati.[/quote]
mislim da bi ovako trebalo:
[latex]\displaystyle\ln (\frac{x}{2})[/latex][latex]*[/latex][latex]\displaystyle\ln (\frac{x}{3})[/latex]=[latex]\displaystyle\((ln{x}-ln2)[/latex][latex]*[/latex][latex]\displaystyle\((ln{x}-ln3)=[/latex]
[latex]=\displaystyle\ln^2{x}-ln{x}ln{3}-ln{x}ln{2}+ln2ln3=[/latex][latex]\displaystyle\ln^2{x}-(ln{3}+ln{2})*lnx+ln2ln3[/latex]
i sad mozemo napraviti kompoziciju:
f=g°h gdje je h=[latex]\displaystyle\ln{x}[/latex] i g=[latex]\displaystyle{x}^2-(ln2+ln3)x+ln2ln3[/latex]
ups netko je bio brži. al nema veze malo sam naučila pisati u latexu :)
| dodoria (napisa): | Zadatak je s popravnog kolokvija, god. 2009./2010., 2., a ide ovako:
f(x)= ln(x/2) * ln(x/3).
Trazi se slika intervala [2,6] i praslika od [-1,0> .
Mislim da je očito da se ova gornja fja. treba prikazati kao kompozicija, odatle je zadatak relativno lagan, ali imam problema upravo s tim. Trebaju mi samo kompozicije, dakle, sami početak, pa ako je netko voljan raspisati taj dio. 
P.S. Nisam još uhvatio korak s korištenjem ovog (La)Tex-a pa sam morao ovako pisati. |
mislim da bi ovako trebalo:
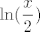  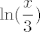 = =  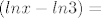
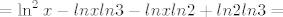 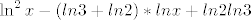
i sad mozemo napraviti kompoziciju:
f=g°h gdje je h=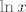 i g= i g=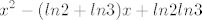
ups netko je bio brži. al nema veze malo sam naučila pisati u latexu 
|
|
| [Vrh] |
|
|








