| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Saf
Forumski umjetnik


Pridružen/a: 10. 06. 2005. (21:55:28)
Postovi: (1B0)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Liddy
Forumaš(ica)


Pridružen/a: 17. 08. 2004. (10:03:41)
Postovi: (169)16
|
|
| [Vrh] |
|
Saf
Forumski umjetnik


Pridružen/a: 10. 06. 2005. (21:55:28)
Postovi: (1B0)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)

Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol: 
|
|
| [Vrh] |
|
lost_soul
Forumaš(ica)
Pridružen/a: 18. 10. 2009. (17:38:41)
Postovi: (133)16
|
|
| [Vrh] |
|
gego
Forumaš(ica)

Pridružen/a: 20. 09. 2009. (21:10:55)
Postovi: (1B)16
Spol: 
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)

Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol: 
|
 Postano: 21:56 čet, 3. 11. 2011 Naslov: Postano: 21:56 čet, 3. 11. 2011 Naslov: |
    |
|
|
Evo još par pitanja, tj. nekih riješenja prošlih kolokvija za koja nisam siguran da su točna, pa ako netko zna di je greška (ako je uopće ima) neka kaže, ili ako je netko siguran da je nešt točno, neka potvrdi...
Prvi zadatak sa figuricama mački i pasa...
http://web.math.hr/~karaga/prvikol1011a.pdf
a) Znači biramo 17 pasa između 32, to je 32 povrh 17, pa još pomnožimo sa brojem kombinacija tih 17 pasa tj. 17!, pa pomnožimo sa 18! zbog mački. Znači to bi bio raspored MPMPMPMPMPMPMPMPMPMPMPMPMPMPMPMPMPM, i sad još trebamo razmjestit ostale pse, gdje gore navedeni skup gledamo kao 1 objekt + 15 pasa što nam je ostalo, pa je to još puta 16!
Znači neko riješenje bi bilo:
(32 povrh 17)*17!*18!*16!
:roll:
Isti kolokvij četvrti zadatak, da li trebamo prebrojavat koliko je brojeva manjih ili jednakih 9 na 10 ili možemo samo lupit da ih ima 9 na 10?
Drugi zadatak na drugoj grupi kolokvija...
Znači 7 studenata + 4 studentice, S1 i S2 moraju skupa sjedit, a S3 i S4 nesmiju bit jedna do druge...
Prvo gledamo koliko ima komb tako da su S1 i S2 jedno pored drugog...
Znači njih uzmemo kao 1 objekt pa nemamo 11 već 10 objekata, te dobijemo preko kružnih permutacija (n-1)! da ih ima 9! i pomnožimo sa 2! zbog permutacije unutar našeg objekta(S1+S2), i onda oduzmemo one u kojima S3 i S4 sjede jedno pored drugog... To je sada isto jedan objekt pa imamo (S1+S2)+(S3+S4)+ ostalih 7=9 objekata, pa je to 8! i pomnožimo sa 2! zbog prvog i 2! zbog drugog skupa.
Znači kao neko riješenje bi bilo:
9!*2!-8!*2!*2!=14*8!
Recimo da je to to, od ovih škakljivijih zadataka...čija su riješenja pod upitnikom...
:shock:
Evo još par pitanja, tj. nekih riješenja prošlih kolokvija za koja nisam siguran da su točna, pa ako netko zna di je greška (ako je uopće ima) neka kaže, ili ako je netko siguran da je nešt točno, neka potvrdi...
Prvi zadatak sa figuricama mački i pasa...
http://web.math.hr/~karaga/prvikol1011a.pdf
a) Znači biramo 17 pasa između 32, to je 32 povrh 17, pa još pomnožimo sa brojem kombinacija tih 17 pasa tj. 17!, pa pomnožimo sa 18! zbog mački. Znači to bi bio raspored MPMPMPMPMPMPMPMPMPMPMPMPMPMPMPMPMPM, i sad još trebamo razmjestit ostale pse, gdje gore navedeni skup gledamo kao 1 objekt + 15 pasa što nam je ostalo, pa je to još puta 16!
Znači neko riješenje bi bilo:
(32 povrh 17)*17!*18!*16!

Isti kolokvij četvrti zadatak, da li trebamo prebrojavat koliko je brojeva manjih ili jednakih 9 na 10 ili možemo samo lupit da ih ima 9 na 10?
Drugi zadatak na drugoj grupi kolokvija...
Znači 7 studenata + 4 studentice, S1 i S2 moraju skupa sjedit, a S3 i S4 nesmiju bit jedna do druge...
Prvo gledamo koliko ima komb tako da su S1 i S2 jedno pored drugog...
Znači njih uzmemo kao 1 objekt pa nemamo 11 već 10 objekata, te dobijemo preko kružnih permutacija (n-1)! da ih ima 9! i pomnožimo sa 2! zbog permutacije unutar našeg objekta(S1+S2), i onda oduzmemo one u kojima S3 i S4 sjede jedno pored drugog... To je sada isto jedan objekt pa imamo (S1+S2)+(S3+S4)+ ostalih 7=9 objekata, pa je to 8! i pomnožimo sa 2! zbog prvog i 2! zbog drugog skupa.
Znači kao neko riješenje bi bilo:
9!*2!-8!*2!*2!=14*8!
Recimo da je to to, od ovih škakljivijih zadataka...čija su riješenja pod upitnikom...

|
|
| [Vrh] |
|
pravipurger
Forumaš(ica)


Pridružen/a: 11. 07. 2009. (10:29:44)
Postovi: (128)16
Spol: 
|
|
| [Vrh] |
|
c4rimson
Forumaš(ica)

Pridružen/a: 11. 01. 2010. (18:57:26)
Postovi: (3B)16
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)

Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol: 
|
 Postano: 8:05 pet, 4. 11. 2011 Naslov: Postano: 8:05 pet, 4. 11. 2011 Naslov: |
    |
|
|
[quote="c4rimson"]Kako u 4. zadatku u grupi b u [url=http://web.math.hr/~karaga/prvikol1011a.pdf]kolokviju[/url] od prosle godine nađemo presjek [latex]A_{1} \cap A_{2} \cap A_{3}[/latex]?[/quote]
Znači da prođeš kroz sva tri segmenta. Da prođeš kroz prvi je jedan način, tada se nalazis u točki (1,1) i gledaš da dođeš do točke (2,2), imaš jednu jedinicu i jednu nulu, to je 2 povrh 1 načina, i onda od (2,3) do (3,3) opet imaš 1 način, a od točke (3,4) imaš samo jedan način do cilja.
Ukupno to je 1*2*1*1=2 načina.
[size=9][color=#999999]Added after 16 minutes:[/color][/size]
[quote="pravipurger"]Ja bi 1a rješio na slj način:
32 psa prvo razmjestimo -> 32! načina
Između njih ili na krajeve mogu doći mačke. Prva na 33 mjesta, druga na 32, ... 18-a na 16 mjesta.
32!*33*32*...*16
2 iz b grupe sam razmišljao kao ti i dobio isto.[/quote]
Hvala, ja sam gledao da je točno jedan pas između mački...što je naravno krivo.
| c4rimson (napisa): | Kako u 4. zadatku u grupi b u kolokviju od prosle godine nađemo presjek 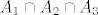 ? ? |
Znači da prođeš kroz sva tri segmenta. Da prođeš kroz prvi je jedan način, tada se nalazis u točki (1,1) i gledaš da dođeš do točke (2,2), imaš jednu jedinicu i jednu nulu, to je 2 povrh 1 načina, i onda od (2,3) do (3,3) opet imaš 1 način, a od točke (3,4) imaš samo jedan način do cilja.
Ukupno to je 1*2*1*1=2 načina.
Added after 16 minutes:
| pravipurger (napisa): | Ja bi 1a rješio na slj način:
32 psa prvo razmjestimo → 32! načina
Između njih ili na krajeve mogu doći mačke. Prva na 33 mjesta, druga na 32, ... 18-a na 16 mjesta.
32!*33*32*...*16
2 iz b grupe sam razmišljao kao ti i dobio isto. |
Hvala, ja sam gledao da je točno jedan pas između mački...što je naravno krivo.
|
|
| [Vrh] |
|
jackass9
Forumaš(ica)

Pridružen/a: 19. 09. 2009. (10:23:58)
Postovi: (15D)16
Spol: 
Lokacija: pod stolom
|
 Postano: 10:57 pet, 4. 11. 2011 Naslov: Postano: 10:57 pet, 4. 11. 2011 Naslov: |
    |
|
|
[quote="gego"][quote="lost_soul"]a nije u zadatku zadano 7 muškaraca i 2 žene?[/quote]
i između žena je 2 muškarca.
meni ispada rjesenje: 7!*3*2*6*3!
imamo raspored : xMMxMMx , na mjestu x dolazi žena. ova 4M možemo rasporediti na 4! načina, 2Ž na 3*2 načina i još nam ostaju 3 muškarca koja možemo premjestiti sva 3 lijevo ili desno, 2 lijevo i 1 desno i 2 desno i 1 lijevo a to je 2*3! + 2*3! + 2*3! = 6*3![/quote]
meni piše da je točno 3 muškarca između 2 žene :)
uglavnom, u slučaju ovog da su 3 muškarca među dvije žene, rješio sam na sljedeći način:
zamislio sam 3 muškarca i 2 žene kao jedan blok u kojem su žene na rubnim pozicijama i ta 3 mužjaka između njih. Unutar toga bloka imamo samo 2 načina za razmještanje jer ženke mogu samo zamijeniti svoje pozicije...sad je ostalo još 4 muškarca i plus ovaj objekt, to možemo rasporediti na 5! načina....
na kraju, po principu produkta, imamo 5!*2=240 načina
ja mislim da je ovo moje dobro :oops:
| gego (napisa): | | lost_soul (napisa): | | a nije u zadatku zadano 7 muškaraca i 2 žene? |
i između žena je 2 muškarca.
meni ispada rjesenje: 7!*3*2*6*3!
imamo raspored : xMMxMMx , na mjestu x dolazi žena. ova 4M možemo rasporediti na 4! načina, 2Ž na 3*2 načina i još nam ostaju 3 muškarca koja možemo premjestiti sva 3 lijevo ili desno, 2 lijevo i 1 desno i 2 desno i 1 lijevo a to je 2*3! + 2*3! + 2*3! = 6*3! |
meni piše da je točno 3 muškarca između 2 žene 
uglavnom, u slučaju ovog da su 3 muškarca među dvije žene, rješio sam na sljedeći način:
zamislio sam 3 muškarca i 2 žene kao jedan blok u kojem su žene na rubnim pozicijama i ta 3 mužjaka između njih. Unutar toga bloka imamo samo 2 načina za razmještanje jer ženke mogu samo zamijeniti svoje pozicije...sad je ostalo još 4 muškarca i plus ovaj objekt, to možemo rasporediti na 5! načina....
na kraju, po principu produkta, imamo 5!*2=240 načina
ja mislim da je ovo moje dobro 
_________________
Nema mozga do malog mozga
|
|
| [Vrh] |
|
gego
Forumaš(ica)

Pridružen/a: 20. 09. 2009. (21:10:55)
Postovi: (1B)16
Spol: 
|
 Postano: 12:53 pet, 4. 11. 2011 Naslov: Postano: 12:53 pet, 4. 11. 2011 Naslov: |
    |
|
|
[quote="jackass9"][quote="gego"][quote="lost_soul"]a nije u zadatku zadano 7 muškaraca i 2 žene?[/quote]
i između žena je 2 muškarca.
meni ispada rjesenje: 7!*3*2*6*3!
imamo raspored : xMMxMMx , na mjestu x dolazi žena. ova 4M možemo rasporediti na 4! načina, 2Ž na 3*2 načina i još nam ostaju 3 muškarca koja možemo premjestiti sva 3 lijevo ili desno, 2 lijevo i 1 desno i 2 desno i 1 lijevo a to je 2*3! + 2*3! + 2*3! = 6*3![/quote]
meni piše da je točno 3 muškarca između 2 žene :)
uglavnom, u slučaju ovog da su 3 muškarca među dvije žene, rješio sam na sljedeći način:
zamislio sam 3 muškarca i 2 žene kao jedan blok u kojem su žene na rubnim pozicijama i ta 3 mužjaka između njih. Unutar toga bloka imamo samo 2 načina za razmještanje jer ženke mogu samo zamijeniti svoje pozicije...sad je ostalo još 4 muškarca i plus ovaj objekt, to možemo rasporediti na 5! načina....
na kraju, po principu produkta, imamo 5!*2=240 načina
ja mislim da je ovo moje dobro :oops:[/quote]
i još možeš 3 muškarca između 2 žene razmjestit na 3! načina
| jackass9 (napisa): | | gego (napisa): | | lost_soul (napisa): | | a nije u zadatku zadano 7 muškaraca i 2 žene? |
i između žena je 2 muškarca.
meni ispada rjesenje: 7!*3*2*6*3!
imamo raspored : xMMxMMx , na mjestu x dolazi žena. ova 4M možemo rasporediti na 4! načina, 2Ž na 3*2 načina i još nam ostaju 3 muškarca koja možemo premjestiti sva 3 lijevo ili desno, 2 lijevo i 1 desno i 2 desno i 1 lijevo a to je 2*3! + 2*3! + 2*3! = 6*3! |
meni piše da je točno 3 muškarca između 2 žene 
uglavnom, u slučaju ovog da su 3 muškarca među dvije žene, rješio sam na sljedeći način:
zamislio sam 3 muškarca i 2 žene kao jedan blok u kojem su žene na rubnim pozicijama i ta 3 mužjaka između njih. Unutar toga bloka imamo samo 2 načina za razmještanje jer ženke mogu samo zamijeniti svoje pozicije...sad je ostalo još 4 muškarca i plus ovaj objekt, to možemo rasporediti na 5! načina....
na kraju, po principu produkta, imamo 5!*2=240 načina
ja mislim da je ovo moje dobro  |
i još možeš 3 muškarca između 2 žene razmjestit na 3! načina
|
|
| [Vrh] |
|
jackass9
Forumaš(ica)

Pridružen/a: 19. 09. 2009. (10:23:58)
Postovi: (15D)16
Spol: 
Lokacija: pod stolom
|
 Postano: 13:27 pet, 4. 11. 2011 Naslov: Postano: 13:27 pet, 4. 11. 2011 Naslov: |
    |
|
|
[quote="gego"][quote="jackass9"][quote="gego"][quote="lost_soul"]a nije u zadatku zadano 7 muškaraca i 2 žene?[/quote]
i između žena je 2 muškarca.
meni ispada rjesenje: 7!*3*2*6*3!
imamo raspored : xMMxMMx , na mjestu x dolazi žena. ova 4M možemo rasporediti na 4! načina, 2Ž na 3*2 načina i još nam ostaju 3 muškarca koja možemo premjestiti sva 3 lijevo ili desno, 2 lijevo i 1 desno i 2 desno i 1 lijevo a to je 2*3! + 2*3! + 2*3! = 6*3![/quote]
meni piše da je točno 3 muškarca između 2 žene :)
uglavnom, u slučaju ovog da su 3 muškarca među dvije žene, rješio sam na sljedeći način:
zamislio sam 3 muškarca i 2 žene kao jedan blok u kojem su žene na rubnim pozicijama i ta 3 mužjaka između njih. Unutar toga bloka imamo samo 2 načina za razmještanje jer ženke mogu samo zamijeniti svoje pozicije...sad je ostalo još 4 muškarca i plus ovaj objekt, to možemo rasporediti na 5! načina....
na kraju, po principu produkta, imamo 5!*2=240 načina
ja mislim da je ovo moje dobro :oops:[/quote]
i još možeš 3 muškarca između 2 žene razmjestit na 3! načina[/quote]
e, to je to :)
| gego (napisa): | | jackass9 (napisa): | | gego (napisa): | | lost_soul (napisa): | | a nije u zadatku zadano 7 muškaraca i 2 žene? |
i između žena je 2 muškarca.
meni ispada rjesenje: 7!*3*2*6*3!
imamo raspored : xMMxMMx , na mjestu x dolazi žena. ova 4M možemo rasporediti na 4! načina, 2Ž na 3*2 načina i još nam ostaju 3 muškarca koja možemo premjestiti sva 3 lijevo ili desno, 2 lijevo i 1 desno i 2 desno i 1 lijevo a to je 2*3! + 2*3! + 2*3! = 6*3! |
meni piše da je točno 3 muškarca između 2 žene 
uglavnom, u slučaju ovog da su 3 muškarca među dvije žene, rješio sam na sljedeći način:
zamislio sam 3 muškarca i 2 žene kao jedan blok u kojem su žene na rubnim pozicijama i ta 3 mužjaka između njih. Unutar toga bloka imamo samo 2 načina za razmještanje jer ženke mogu samo zamijeniti svoje pozicije...sad je ostalo još 4 muškarca i plus ovaj objekt, to možemo rasporediti na 5! načina....
na kraju, po principu produkta, imamo 5!*2=240 načina
ja mislim da je ovo moje dobro  |
i još možeš 3 muškarca između 2 žene razmjestit na 3! načina |
e, to je to 
_________________
Nema mozga do malog mozga
|
|
| [Vrh] |
|
|














