| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Megy Poe
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (23:14:52)
Postovi: (122)16
|
 Postano: 21:47 sri, 14. 12. 2011 Naslov: Postano: 21:47 sri, 14. 12. 2011 Naslov: |
    |
|
|
Hvala. Jel znaš 4.42 i u b) 4.46 oni računaju ovako: očekivani broj gubitaka nakon 4. igre je točno 1, dakle, traženo očekivanje je zapravo jednako očekivanom broju gubitaka u prve 4 igre uvećanom za 1. Očekivani broj gubitaka u prve 4 igre je zapravo očekivanje slučajne varijable koja poprima vrijednosti k={0,1,2,3,4} s vjerojatnostima [latex]{4 \choose k} \cdot \left(1-p\right)^k \cdot p^{4-k}[/latex] i onda se dobije oćekivanje 5-4p kao što je i u rješenjima, al zašto se negleda da recimo nema gubitka u prvih 5 igara tj da se igra i nakon pete sve dok se ne izgubi?
Hvala. Jel znaš 4.42 i u b) 4.46 oni računaju ovako: očekivani broj gubitaka nakon 4. igre je točno 1, dakle, traženo očekivanje je zapravo jednako očekivanom broju gubitaka u prve 4 igre uvećanom za 1. Očekivani broj gubitaka u prve 4 igre je zapravo očekivanje slučajne varijable koja poprima vrijednosti k={0,1,2,3,4} s vjerojatnostima 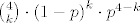 i onda se dobije oćekivanje 5-4p kao što je i u rješenjima, al zašto se negleda da recimo nema gubitka u prvih 5 igara tj da se igra i nakon pete sve dok se ne izgubi? i onda se dobije oćekivanje 5-4p kao što je i u rješenjima, al zašto se negleda da recimo nema gubitka u prvih 5 igara tj da se igra i nakon pete sve dok se ne izgubi?
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
Megy Poe
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (23:14:52)
Postovi: (122)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
Joker
Forumaš(ica)

Pridružen/a: 19. 09. 2010. (10:19:16)
Postovi: (8C)16
Spol: 
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
|
| [Vrh] |
|
888
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (18:26:14)
Postovi: (29)16
|
|
| [Vrh] |
|
mono
Forumaš(ica)
Pridružen/a: 16. 09. 2011. (13:04:01)
Postovi: (E)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 19:31 ned, 15. 1. 2012 Naslov: Postano: 19:31 ned, 15. 1. 2012 Naslov: |
    |
|
|
@mono
Pa, ideja je ovakva...
Neka je X = broj pegaza koje je vještica dobila
Prilično je jasno da je to binomna slučajna varijabla [latex]X \sim B(n, 0.2)[/latex].
I tebe zanima koji je najmanji n za kojeg vrijedi:
[latex]P(5X + 2(n-X) \geq 1000) \geq 0.95[/latex] (Zašto?)
Dalje se ide poprilično standardnim postupkom aproksimacije binomne sl. varijable sa normalnom distribucijom i na kraju dobiješ jednadžbu sa n... Pitaj ako ti nešto od ovoga nije jasno.
@888
Pa, prvo izračunaš vjerojatnosti [latex]P(X=0), P(X=1), P(X=2)[/latex] isto tako za Y - u dva izvlačenja možeš izvući jednu, dvije ili nijednu bijelu kuglicu.
I onda se prisjeti kako se definira funkcija distribucije. :D
Samo reci ako ti još uvijek nije jasno :)
@mono
Pa, ideja je ovakva...
Neka je X = broj pegaza koje je vještica dobila
Prilično je jasno da je to binomna slučajna varijabla 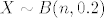 . .
I tebe zanima koji je najmanji n za kojeg vrijedi:
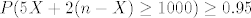 (Zašto?) (Zašto?)
Dalje se ide poprilično standardnim postupkom aproksimacije binomne sl. varijable sa normalnom distribucijom i na kraju dobiješ jednadžbu sa n... Pitaj ako ti nešto od ovoga nije jasno.
@888
Pa, prvo izračunaš vjerojatnosti 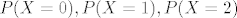 isto tako za Y - u dva izvlačenja možeš izvući jednu, dvije ili nijednu bijelu kuglicu. isto tako za Y - u dva izvlačenja možeš izvući jednu, dvije ili nijednu bijelu kuglicu.
I onda se prisjeti kako se definira funkcija distribucije. 
Samo reci ako ti još uvijek nije jasno 
|
|
| [Vrh] |
|
mono
Forumaš(ica)
Pridružen/a: 16. 09. 2011. (13:04:01)
Postovi: (E)16
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
|
| [Vrh] |
|
Megy Poe
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (23:14:52)
Postovi: (122)16
|
|
| [Vrh] |
|
kobila krsto
Forumaš(ica)
Pridružen/a: 02. 07. 2009. (16:55:08)
Postovi: (6A)16
|
|
| [Vrh] |
|
888
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (18:26:14)
Postovi: (29)16
|
|
| [Vrh] |
|
Megy Poe
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (23:14:52)
Postovi: (122)16
|
 Postano: 15:37 pon, 16. 1. 2012 Naslov: Postano: 15:37 pon, 16. 1. 2012 Naslov: |
    |
|
|
[quote="888"][quote="Megy Poe"]Da li bi netko mogao pomoći sa 6.47? meni je x~B(50,1/37), i tražim P(x>50/2) al ne ispada mi dobro rješenje...Šta radim krivo?
[size=9][color=#999999]Added after 23 minutes:[/color][/size]
Nasla sam si grešku, ispričavam se, možda ipak nije pametno učiti u 4 ujutro[/quote]
koliko ti bude rezultat?[/quote]
Isto ko u rješenjima al ako si možda prepisao ovo moje s foruma tj tako riješavao možda ti je zato krivo, u tom je zapravo greška, jer treba biti B~(50, 18/37)
| 888 (napisa): | | Megy Poe (napisa): | Da li bi netko mogao pomoći sa 6.47? meni je x~B(50,1/37), i tražim P(x>50/2) al ne ispada mi dobro rješenje...Šta radim krivo?
Added after 23 minutes:
Nasla sam si grešku, ispričavam se, možda ipak nije pametno učiti u 4 ujutro |
koliko ti bude rezultat? |
Isto ko u rješenjima al ako si možda prepisao ovo moje s foruma tj tako riješavao možda ti je zato krivo, u tom je zapravo greška, jer treba biti B~(50, 18/37)
|
|
| [Vrh] |
|
Joker
Forumaš(ica)

Pridružen/a: 19. 09. 2010. (10:19:16)
Postovi: (8C)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
|










