|
[quote="Matematicar"]
Poznato je da je vjerojatnost pogotka mete u svakom od n pokušaja jednaka i iznosi
0, 4 p = . [/quote]
Ovdje vjerojatno misliš [latex]p=0.4[/latex].
U tom slučaju, za (a) i (b) zadatak, neka je [latex]X[/latex] slučajna varijabla koja predstavlja broj pogodaka u [latex]1500[/latex] gađanja mete. Tada je [latex]X \sim B(1500,0.4)[/latex], što možemo aproksimirati normalnom slučajnom varijablom sa očekivanjem [latex]\mu=np[/latex] i varijancom [latex]\sigma^2=npq[/latex], dakle [latex]X\sim N(600,360)[/latex].
[b](a) [/b]
[latex]1500 \cdot 0.4 = 600[/latex]
[latex]1500 \cdot 0.02 = 30[/latex]
Tražena vjerojatnost je
[latex]P(600-30 < X < 600+30) = P(570<X<630) = \Phi (\frac{630-600}{\sqrt{360}}) - \Phi (\frac{570-600}{\sqrt{360}}) \approx 2\cdot \Phi(1.58) - 1 \approx 2\cdot 0.9429 - 1 = 0.8858 = 88,58\%.[/latex]
[b](b)[/b]
[latex]P(611 \leq X \leq 637) = \Phi (\frac{637-600}{\sqrt{360}}) - \Phi (\frac{611-600}{\sqrt{360}}) \approx \Phi(1.95) - \Phi(0.58) \approx 0.9744-0.719 = 0.2554 = 25,54\%.[/latex]
[b](c)[/b]
Neka je [latex]Y[/latex] slučajna varijabla koja predstavlja broj pogodaka u [latex]2400[/latex] gađanja. Tada je [latex]Y \sim B(2400,0.4)[/latex], odnosno kad aproksimiramo normalnom slučajnom varijablom, [latex]Y \sim N(960,576)[/latex].
Označimo sa [latex]y[/latex] odstupanje od očekivanja, takvo da je
[latex]P(960-y \leq Y \leq 960+y) = 0.992[/latex]
[latex]\Rightarrow 2\cdot \Phi(\frac{(960+y)-960}{\sqrt{576}})-1 = 0.992[/latex]
[latex]\Rightarrow \Phi(\frac{y}{24}) = 0.996[/latex]
[latex]\Rightarrow \frac{y}{24}=2.65[/latex]
[latex]\Rightarrow y = 63.6[/latex]
[latex]\Rightarrow P(960-63.6 \leq Y \leq 960+63.6) = 0.992[/latex]
[latex]\Rightarrow P(Y \in [896.4,1023.6]) = 0.992.[/latex]
[b](d)[/b]
Ovdje ne razumijem što ti znači ovo "10-2", ali označimo tu razliku sa [latex]s[/latex], i označimo traženi broj gađanja mete sa [latex]n[/latex]. Sada imamo slučajnu varijablu [latex]Z\sim B(n,0.4)[/latex], odnosno [latex]Z\sim N(0.4n, 0.24n)[/latex], za koju vrijedi slično kao u (a) dijelu zadatka:
[latex]P(0.4n-sn < Z < 0.4n+sn) = 0.95[/latex]
[latex]\Rightarrow 2\cdot\Phi(\frac{sn}{\sqrt{0.24n}})-1=0.95[/latex]
[latex]\Rightarrow \Phi(\frac{sn}{\sqrt{0.24n}}) = 0.975[/latex]
[latex]\Rightarrow \frac{sn}{\sqrt{0.24n}} = 1.96[/latex]
[latex]\Rightarrow \dots \Rightarrow n \approx \frac{0.9216}{s^2}.[/latex]
I sad samo umjesto [latex]s[/latex] uvrsti ono iz teksta zadatka što ja nisam uspio dešifrirati. Znači npr. ako je [latex]s=0.02[/latex], tada je [latex]n=2304[/latex], itd.
| Matematicar (napisa): |
Poznato je da je vjerojatnost pogotka mete u svakom od n pokušaja jednaka i iznosi
0, 4 p = . |
Ovdje vjerojatno misliš 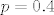 . .
U tom slučaju, za (a) i (b) zadatak, neka je  slučajna varijabla koja predstavlja broj pogodaka u slučajna varijabla koja predstavlja broj pogodaka u  gađanja mete. Tada je gađanja mete. Tada je 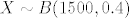 , što možemo aproksimirati normalnom slučajnom varijablom sa očekivanjem , što možemo aproksimirati normalnom slučajnom varijablom sa očekivanjem 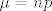 i varijancom i varijancom 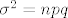 , dakle , dakle 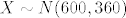 . .
(a)
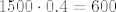
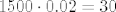
Tražena vjerojatnost je
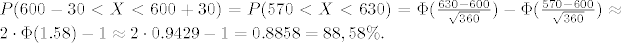
(b)
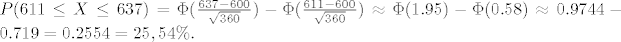
(c)
Neka je 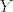 slučajna varijabla koja predstavlja broj pogodaka u slučajna varijabla koja predstavlja broj pogodaka u 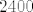 gađanja. Tada je gađanja. Tada je 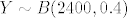 , odnosno kad aproksimiramo normalnom slučajnom varijablom, , odnosno kad aproksimiramo normalnom slučajnom varijablom,  . .
Označimo sa  odstupanje od očekivanja, takvo da je odstupanje od očekivanja, takvo da je
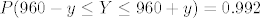
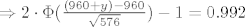
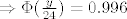
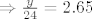

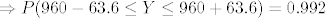
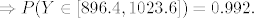
(d)
Ovdje ne razumijem što ti znači ovo "10-2", ali označimo tu razliku sa  , i označimo traženi broj gađanja mete sa , i označimo traženi broj gađanja mete sa  . Sada imamo slučajnu varijablu . Sada imamo slučajnu varijablu 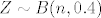 , odnosno , odnosno 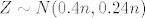 , za koju vrijedi slično kao u (a) dijelu zadatka: , za koju vrijedi slično kao u (a) dijelu zadatka:
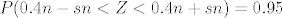
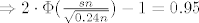
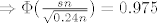
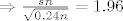
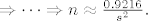
I sad samo umjesto  uvrsti ono iz teksta zadatka što ja nisam uspio dešifrirati. Znači npr. ako je uvrsti ono iz teksta zadatka što ja nisam uspio dešifrirati. Znači npr. ako je 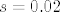 , tada je , tada je 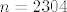 , itd. , itd.
|





