| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
aj_ca_volin_te
Forumaš(ica)


Pridružen/a: 22. 11. 2011. (20:18:49)
Postovi: (6F)16
|
|
| [Vrh] |
|
simon11
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (21:02:52)
Postovi: (7C)16
Spol: 
Lokacija: FunkyTown
|
|
| [Vrh] |
|
PermutiranoPrase
Forumaš(ica)


Pridružen/a: 10. 09. 2011. (16:08:19)
Postovi: (F4)16
Spol: 
|
 Postano: 18:55 pet, 6. 1. 2012 Naslov: Postano: 18:55 pet, 6. 1. 2012 Naslov: |
    |
|
|
[quote="mornik"]Evo, grupa 1.
4. zadatak, a):
Izlučimo [latex]e^{\sin x}[/latex] iz brojnika i [latex]e^x[/latex] iz nazivnika - dobivamo da tražimo limes od [latex]\displaystyle\frac{e^{\sin x}}{e^x}\cdot \frac{1-e^{\sin x}}{1-e^x}[/latex]. Ovo ti vjerojatno već sliči na nešto razumno. Sad još pomnoži i brojnik i nazivnik s [latex]x\sin x[/latex] i upari članove da bi dobio/dobila limese koje poznaješ. Reci ako imaš problema s ovim zadnjim dijelom - mislim da bi finalno rješenje trebalo ispasti jedno cijelo :).[/quote]
Radi se o [url=http://web.math.pmf.unizg.hr/nastava/analiza/kol/ma1-0708-kol2.pdf]kolokviju 2008[/url]. Sve ovo ima smisla da piše [tex]sin^2x[/tex], ali kako je sin(2x), pretpostavljam da ima neka druga caka? (Ja sam raspisivala, ali nikud stigla). :?
Kao ni sa 4.a) zadatkom iz druge grupe... Kako god da raspišem, uvijek mi ostane u nekom neodređenom obliku, npr. ostane mi 1/x, a x-->0 i sl. Ako tko uspije, nek javi kad stigne. Nadam se da ću uspjeti bar u zadatku iz 3.grupe. :(
| mornik (napisa): | Evo, grupa 1.
4. zadatak, a):
Izlučimo 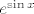 iz brojnika i iz brojnika i 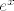 iz nazivnika - dobivamo da tražimo limes od iz nazivnika - dobivamo da tražimo limes od  . Ovo ti vjerojatno već sliči na nešto razumno. Sad još pomnoži i brojnik i nazivnik s . Ovo ti vjerojatno već sliči na nešto razumno. Sad još pomnoži i brojnik i nazivnik s 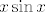 i upari članove da bi dobio/dobila limese koje poznaješ. Reci ako imaš problema s ovim zadnjim dijelom - mislim da bi finalno rješenje trebalo ispasti jedno cijelo i upari članove da bi dobio/dobila limese koje poznaješ. Reci ako imaš problema s ovim zadnjim dijelom - mislim da bi finalno rješenje trebalo ispasti jedno cijelo  . . |
Radi se o kolokviju 2008. Sve ovo ima smisla da piše [tex]sin^2x[/tex], ali kako je sin(2x), pretpostavljam da ima neka druga caka? (Ja sam raspisivala, ali nikud stigla). 
Kao ni sa 4.a) zadatkom iz druge grupe... Kako god da raspišem, uvijek mi ostane u nekom neodređenom obliku, npr. ostane mi 1/x, a x→0 i sl. Ako tko uspije, nek javi kad stigne. Nadam se da ću uspjeti bar u zadatku iz 3.grupe. 
Zadnja promjena: PermutiranoPrase; 20:40 pet, 6. 1. 2012; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
|
| [Vrh] |
|
quark
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: 
|
 Postano: 0:40 sub, 7. 1. 2012 Naslov: Postano: 0:40 sub, 7. 1. 2012 Naslov: |
    |
|
|
[quote="PermutiranoPrase"]
Radi se o [url=http://web.math.pmf.unizg.hr/nastava/analiza/kol/ma1-0708-kol2.pdf]kolokviju 2008[/url]. Sve ovo ima smisla da piše [tex]sin^2x[/tex], ali kako je sin(2x), pretpostavljam da ima neka druga caka? (Ja sam raspisivala, ali nikud stigla). :?
Kao ni sa 4.a) zadatkom iz druge grupe... Kako god da raspišem, uvijek mi ostane u nekom neodređenom obliku, npr. ostane mi 1/x, a x-->0 i sl. Ako tko uspije, nek javi kad stigne. Nadam se da ću uspjeti bar u zadatku iz 3.grupe. :([/quote]
Jooj, nije ti komplicirano, nego samo malo naporno :lol:
Namještaš na tablični limes sa e^x, x->0, cijelo vrijeme. Prvo sredi brojnik (dakle, rastaviš na dva razlomka da u brojniku budu jedinice); onda u oba ta nazivnika opet isti trik (rastavljati u dva razlomka...); onda namjestiš sinuse koji su ti ostali od prethodnog namještanja i konačno, zbrojiti dva razlomka i dobije se 1 :)
[size=9]P.S. Zar to nije prva grupa?[/size]
| PermutiranoPrase (napisa): |
Radi se o kolokviju 2008. Sve ovo ima smisla da piše [tex]sin^2x[/tex], ali kako je sin(2x), pretpostavljam da ima neka druga caka? (Ja sam raspisivala, ali nikud stigla). 
Kao ni sa 4.a) zadatkom iz druge grupe... Kako god da raspišem, uvijek mi ostane u nekom neodređenom obliku, npr. ostane mi 1/x, a x→0 i sl. Ako tko uspije, nek javi kad stigne. Nadam se da ću uspjeti bar u zadatku iz 3.grupe.  |
Jooj, nije ti komplicirano, nego samo malo naporno 
Namještaš na tablični limes sa e^x, x→0, cijelo vrijeme. Prvo sredi brojnik (dakle, rastaviš na dva razlomka da u brojniku budu jedinice); onda u oba ta nazivnika opet isti trik (rastavljati u dva razlomka...); onda namjestiš sinuse koji su ti ostali od prethodnog namještanja i konačno, zbrojiti dva razlomka i dobije se 1 
P.S. Zar to nije prva grupa?
Zadnja promjena: quark; 0:43 sub, 7. 1. 2012; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
BlameGame
Forumaš(ica)

Pridružen/a: 14. 09. 2011. (19:17:53)
Postovi: (6C)16
|
|
| [Vrh] |
|
quark
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: 
|
|
| [Vrh] |
|
matematičarka
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:19:07)
Postovi: (38)16
Lokacija: Planet Zemlja
|
|
| [Vrh] |
|
BlameGame
Forumaš(ica)

Pridružen/a: 14. 09. 2011. (19:17:53)
Postovi: (6C)16
|
|
| [Vrh] |
|
quark
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: 
|
|
| [Vrh] |
|
matematičarka
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:19:07)
Postovi: (38)16
Lokacija: Planet Zemlja
|
|
| [Vrh] |
|
quark
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: 
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
 Postano: 1:21 sub, 7. 1. 2012 Naslov: Postano: 1:21 sub, 7. 1. 2012 Naslov: |
    |
|
|
[quote="matematičarka"][quote="quark"][url]http://www4c.wolframalpha.com/Calculate/MSP/MSP663919igbhfe22b7h2250000493e944d6ff6e0ad?MSPStoreType=image/gif&s=48&w=183&h=46[/url] :?:[/quote]
http://www.wolframalpha.com/input/?i=lim%28%281%2B1%2F3%2B1%2F5%2B1%2F7%2B...%2B1%2F%282n-1%29%29%2Flnn%29+n+to+infinity[/quote]
Ne možeš sume tako unositi u Wolfram Alpha, on ih neće "dobro" prepoznati, tj. on to drugačije interpretira.
Dobro je satja riješio.
Preporučam ne koristiti Wolfram Alphu u ovim zadacima kada imate takve nekakve sume ili produkte...
Ja mislim da Wolfram alpha tretira tu sumu u brojniku kao konačnu sumu, tj. kao konačan broj iz skupa realnih brojeva, dok, kad n teži u beskonačnost, i ln n teži u beskonačnost pa je realni broj kroz beskonačnost "jednako" nula.
Ugl, satja je dobro riješio, a Wolfram Alpha u ovom primjeru laže! :P
EDIT: Eto, quark je to malo bolje objasnio od mene i preciznije :P
Ne možeš sume tako unositi u Wolfram Alpha, on ih neće "dobro" prepoznati, tj. on to drugačije interpretira.
Dobro je satja riješio.
Preporučam ne koristiti Wolfram Alphu u ovim zadacima kada imate takve nekakve sume ili produkte...
Ja mislim da Wolfram alpha tretira tu sumu u brojniku kao konačnu sumu, tj. kao konačan broj iz skupa realnih brojeva, dok, kad n teži u beskonačnost, i ln n teži u beskonačnost pa je realni broj kroz beskonačnost "jednako" nula.
Ugl, satja je dobro riješio, a Wolfram Alpha u ovom primjeru laže! 
EDIT: Eto, quark je to malo bolje objasnio od mene i preciznije 
|
|
| [Vrh] |
|
matematičarka
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:19:07)
Postovi: (38)16
Lokacija: Planet Zemlja
|
|
| [Vrh] |
|
quark
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: 
|
|
| [Vrh] |
|
PermutiranoPrase
Forumaš(ica)


Pridružen/a: 10. 09. 2011. (16:08:19)
Postovi: (F4)16
Spol: 
|
 Postano: 10:06 sub, 7. 1. 2012 Naslov: Postano: 10:06 sub, 7. 1. 2012 Naslov: |
    |
|
|
[quote="quark"]
Jooj, nije ti komplicirano, nego samo malo naporno :lol:
Namještaš na tablični limes sa e^x, x->0, cijelo vrijeme. Prvo sredi brojnik (dakle, rastaviš na dva razlomka da u brojniku budu jedinice); onda u oba ta nazivnika opet isti trik (rastavljati u dva razlomka...); onda namjestiš sinuse koji su ti ostali od prethodnog namještanja i konačno, zbrojiti dva razlomka i dobije se 1 :)
[size=9]P.S. Zar to nije prva grupa?[/size][/quote]
Idem pokušati, možda ovaj put uspijem, konačno (4.a) iz 2008. me neće i neće, nijedna grupa, nikako).
| quark (napisa): |
Jooj, nije ti komplicirano, nego samo malo naporno 
Namještaš na tablični limes sa e^x, x→0, cijelo vrijeme. Prvo sredi brojnik (dakle, rastaviš na dva razlomka da u brojniku budu jedinice); onda u oba ta nazivnika opet isti trik (rastavljati u dva razlomka...); onda namjestiš sinuse koji su ti ostali od prethodnog namještanja i konačno, zbrojiti dva razlomka i dobije se 1 
P.S. Zar to nije prva grupa? |
Idem pokušati, možda ovaj put uspijem, konačno (4.a) iz 2008. me neće i neće, nijedna grupa, nikako).
|
|
| [Vrh] |
|
matematičarka
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:19:07)
Postovi: (38)16
Lokacija: Planet Zemlja
|
|
| [Vrh] |
|
PermutiranoPrase
Forumaš(ica)


Pridružen/a: 10. 09. 2011. (16:08:19)
Postovi: (F4)16
Spol: 
|
 Postano: 13:14 sub, 7. 1. 2012 Naslov: Postano: 13:14 sub, 7. 1. 2012 Naslov: |
    |
|
|
Ponovno žicam pomoć... :oops:
[url=http://www.wolframalpha.com/input/?i=log_2+%28%2810m*n%29%2F%282m%2B5n%29%5E2]Ovo[/url] nisam uspjela riješiti. Traži se supremum i infimum (ako postoje). To je 3.iz kolokvija 2006., (vjerojatno) 3.grupa.
Kaže da ne postoji infimum. Ako uzmem fiksni n ili ili n=m=1, za tako definirani niz dobijem [tex]\lim_{m \to \infty}log_2 \frac {10mn}{(2m+5n)^2} = log_2 \lim_{m \to \infty} \frac {10mn}{(2m+5n)^2} = log_2(0)[/tex], a to baš i ne valja. Mogu li onda reći da zbog toga infimum ne postoji, odnosno da je -beskonačno?
Kaže i da je supremum -2... A kako je on došao do toga i kako bi ja mogla doći do toga, nemam blagog pojma... :shock:
[size=9][color=#999999]Added after 37 minutes:[/color][/size]
[quote="simon11"][size=24] [latex] \lim\limits_{n \to \infty}{\sqrt[n]{shn+1}} [/latex] [/size]
molio bih ako netko moze s postupkom ja ga rastavim ali nikako ne mogu dobiti da je e koliko mi alpha izbacuje[/quote]
Pokušavala sam još jučer, nikako išlo, a sad riješila u 2 reda, prebanalan je: :)
[dtex]\lim_{n} \sqrt[n]{shn+1} = \lim_{n} ((shn+1)^\frac {1}{shn})^\frac{shn}{n} = e^1 = e [/dtex]
Ponovno žicam pomoć... 
Ovo nisam uspjela riješiti. Traži se supremum i infimum (ako postoje). To je 3.iz kolokvija 2006., (vjerojatno) 3.grupa.
Kaže da ne postoji infimum. Ako uzmem fiksni n ili ili n=m=1, za tako definirani niz dobijem [tex]\lim_{m \to \infty}log_2 \frac {10mn}{(2m+5n)^2} = log_2 \lim_{m \to \infty} \frac {10mn}{(2m+5n)^2} = log_2(0)[/tex], a to baš i ne valja. Mogu li onda reći da zbog toga infimum ne postoji, odnosno da je -beskonačno?
Kaže i da je supremum -2... A kako je on došao do toga i kako bi ja mogla doći do toga, nemam blagog pojma... 
Added after 37 minutes:
| simon11 (napisa): | 
molio bih ako netko moze s postupkom ja ga rastavim ali nikako ne mogu dobiti da je e koliko mi alpha izbacuje |
Pokušavala sam još jučer, nikako išlo, a sad riješila u 2 reda, prebanalan je: 
[dtex]\lim_{n} \sqrt[n]{shn+1} = \lim_{n} ((shn+1)^\frac {1}{shn})^\frac{shn}{n} = e^1 = e [/dtex]
|
|
| [Vrh] |
|
simon11
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (21:02:52)
Postovi: (7C)16
Spol: 
Lokacija: FunkyTown
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 14:33 sub, 7. 1. 2012 Naslov: Postano: 14:33 sub, 7. 1. 2012 Naslov: |
    |
|
|
[quote="PermutiranoPrase"]Ponovno žicam pomoć... :oops:
[url=http://www.wolframalpha.com/input/?i=log_2+%28%2810m*n%29%2F%282m%2B5n%29%5E2]Ovo[/url] nisam uspjela riješiti. Traži se supremum i infimum (ako postoje). To je 3.iz kolokvija 2006., (vjerojatno) 3.grupa.
Kaže da ne postoji infimum. Ako uzmem fiksni n ili ili n=m=1, za tako definirani niz dobijem [tex]\lim_{m \to \infty}log_2 \frac {10mn}{(2m+5n)^2} = log_2 \lim_{m \to \infty} \frac {10mn}{(2m+5n)^2} = log_2(0)[/tex], a to baš i ne valja. Mogu li onda reći da zbog toga infimum ne postoji, odnosno da je -beskonačno?
Kaže i da je supremum -2... A kako je on došao do toga i kako bi ja mogla doći do toga, nemam blagog pojma... :shock: [/quote]
Pogledaj 2. post u http://degiorgi.math.hr/forum/viewtopic.php?p=147580
| PermutiranoPrase (napisa): | Ponovno žicam pomoć... 
Ovo nisam uspjela riješiti. Traži se supremum i infimum (ako postoje). To je 3.iz kolokvija 2006., (vjerojatno) 3.grupa.
Kaže da ne postoji infimum. Ako uzmem fiksni n ili ili n=m=1, za tako definirani niz dobijem [tex]\lim_{m \to \infty}log_2 \frac {10mn}{(2m+5n)^2} = log_2 \lim_{m \to \infty} \frac {10mn}{(2m+5n)^2} = log_2(0)[/tex], a to baš i ne valja. Mogu li onda reći da zbog toga infimum ne postoji, odnosno da je -beskonačno?
Kaže i da je supremum -2... A kako je on došao do toga i kako bi ja mogla doći do toga, nemam blagog pojma...  |
Pogledaj 2. post u http://degiorgi.math.hr/forum/viewtopic.php?p=147580
_________________
The Dude Abides
|
|
| [Vrh] |
|
|















